Computing Intraclass Correlations (ICC) as Estimates of Interrater Reliability in SPSS
 If you think my writing about statistics is clear below, consider my student-centered, practical and concise Step-by-Step Introduction to Statistics for Business for your undergraduate classes, available now from SAGE. Social scientists of all sorts will appreciate the ordinary, approachable language and practical value – each chapter starts with and discusses a young small business owner facing a problem solvable with statistics, a problem solved by the end of the chapter with the statistical kung-fu gained.
If you think my writing about statistics is clear below, consider my student-centered, practical and concise Step-by-Step Introduction to Statistics for Business for your undergraduate classes, available now from SAGE. Social scientists of all sorts will appreciate the ordinary, approachable language and practical value – each chapter starts with and discusses a young small business owner facing a problem solvable with statistics, a problem solved by the end of the chapter with the statistical kung-fu gained.
This article has been published in the Winnower. You can cite it as:
Landers, R.N. (2015). Computing intraclass correlations (ICC) as estimates of interrater reliability in SPSS. The Winnower 2:e143518.81744. DOI: 10.15200/winn.143518.81744
You can also download the published version as a PDF by clicking here.
![]() Recently, a colleague of mine asked for some advice on how to compute interrater reliability for a coding task, and I discovered that there aren’t many resources online written in an easy-to-understand format – most either 1) go in depth about formulas and computation or 2) go in depth about SPSS without giving many specific reasons for why you’d make several important decisions. The primary resource available is a 1979 paper by Shrout and Fleiss1, which is quite dense. So I am taking a stab at providing a comprehensive but easier-to-understand resource.
Recently, a colleague of mine asked for some advice on how to compute interrater reliability for a coding task, and I discovered that there aren’t many resources online written in an easy-to-understand format – most either 1) go in depth about formulas and computation or 2) go in depth about SPSS without giving many specific reasons for why you’d make several important decisions. The primary resource available is a 1979 paper by Shrout and Fleiss1, which is quite dense. So I am taking a stab at providing a comprehensive but easier-to-understand resource.
Reliability, generally, is the proportion of “real” information about a construct of interest captured by your measurement of it. For example, if someone reported the reliability of their measure was .8, you could conclude that 80% of the variability in the scores captured by that measure represented the construct, and 20% represented random variation. The more uniform your measurement, the higher reliability will be.
In the social sciences, we often have research participants complete surveys, in which case you don’t need ICCs – you would more typically use coefficient alpha. But when you have research participants provide something about themselves from which you need to extract data, your measurement becomes what you get from that extraction. For example, in one of my lab’s current studies, we are collecting copies of Facebook profiles from research participants, after which a team of lab assistants looks them over and makes ratings based upon their content. This process is called coding. Because the research assistants are creating the data, their ratings are my scale – not the original data. Which means they 1) make mistakes and 2) vary in their ability to make those ratings. An estimate of interrater reliability will tell me what proportion of their ratings is “real”, i.e. represents an underlying construct (or potentially a combination of constructs – there is no way to know from reliability alone – all you can conclude is that you are measuring something consistently).
An intraclass correlation (ICC) can be a useful estimate of inter-rater reliability on quantitative data because it is highly flexible. A Pearson correlation can be a valid estimator of interrater reliability, but only when you have meaningful pairings between two and only two raters. What if you have more? What if your raters differ by ratee? This is where ICC comes in (note that if you have qualitative data, e.g. categorical data or ranks, you would not use ICC).
Unfortunately, this flexibility makes ICC a little more complicated than many estimators of reliability. While you can often just throw items into SPSS to compute a coefficient alpha on a scale measure, there are several additional questions one must ask when computing an ICC, and one restriction. The restriction is straightforward: you must have the same number of ratings for every case rated. The questions are more complicated, and their answers are based upon how you identified your raters, and what you ultimately want to do with your reliability estimate. Here are the first two questions:
- Do you have consistent raters for all ratees? For example, do the exact same 8 raters make ratings on every ratee?
- Do you have a sample or population of raters?
If your answer to Question 1 is no, you need ICC(1). In SPSS, this is called “One-Way Random.” In coding tasks, this is uncommon, since you can typically control the number of raters fairly carefully. It is most useful with massively large coding tasks. For example, if you had 2000 ratings to make, you might assign your 10 research assistants to make 400 ratings each – each research assistant makes ratings on 2 ratees (you always have 2 ratings per case), but you counterbalance them so that a random two raters make ratings on each subject. It’s called “One-Way Random” because 1) it makes no effort to disentangle the effects of the rater and ratee (i.e. one effect) and 2) it assumes these ratings are randomly drawn from a larger populations (i.e. a random effects model). ICC(1) will always be the smallest of the ICCs.
If your answer to Question 1 is yes and your answer to Question 2 is “sample”, you need ICC(2). In SPSS, this is called “Two-Way Random.” Unlike ICC(1), this ICC assumes that the variance of the raters is only adding noise to the estimate of the ratees, and that mean rater error = 0. Or in other words, while a particular rater might rate Ratee 1 high and Ratee 2 low, it should all even out across many raters. Like ICC(1), it assumes a random effects model for raters, but it explicitly models this effect – you can sort of think of it like “controlling for rater effects” when producing an estimate of reliability. If you have the same raters for each case, this is generally the model to go with. This will always be larger than ICC(1) and is represented in SPSS as “Two-Way Random” because 1) it models both an effect of rater and of ratee (i.e. two effects) and 2) assumes both are drawn randomly from larger populations (i.e. a random effects model).
If your answer to Question 1 is yes and your answer to Question 2 is “population”, you need ICC(3). In SPSS, this is called “Two-Way Mixed.” This ICC makes the same assumptions as ICC(2), but instead of treating rater effects as random, it treats them as fixed. This means that the raters in your task are the only raters anyone would be interested in. This is uncommon in coding, because theoretically your research assistants are only a few of an unlimited number of people that could make these ratings. This means ICC(3) will also always be larger than ICC(1) and typically larger than ICC(2), and is represented in SPSS as “Two-Way Mixed” because 1) it models both an effect of rater and of ratee (i.e. two effects) and 2) assumes a random effect of ratee but a fixed effect of rater (i.e. a mixed effects model).
After you’ve determined which kind of ICC you need, there is a second decision to be made: are you interested in the reliability of a single rater, or of their mean? If you’re coding for research, you’re probably going to use the mean rating. If you’re coding to determine how accurate a single person would be if they made the ratings on their own, you’re interested in the reliability of a single rater. For example, in our Facebook study, we want to know both. First, we might ask “what is the reliability of our ratings?” Second, we might ask “if one person were to make these judgments from a Facebook profile, how accurate would that person be?” We add “,k” to the ICC rating when looking at means, or “,1” when looking at the reliability of single raters. For example, if you computed an ICC(2) with 8 raters, you’d be computing ICC(2,8). If you computed an ICC(1) with the same 16 raters for every case but were interested in a single rater, you’d still be computing ICC(2,1). For ICC(#,1), a large number of raters will produce a narrower confidence interval around your reliability estimate than a small number of raters, which is why you’d still want a large number of raters, if possible, when estimating ICC(#,1).
After you’ve determined which specificity you need, the third decision is to figure out whether you need a measure of absolute agreement or consistency. If you’ve studied correlation, you’re probably already familiar with this concept: if two variables are perfectly consistent, they don’t necessarily agree. For example, consider Variable 1 with values 1, 2, 3 and Variable 2 with values 7, 8, 9. Even though these scores are very different, the correlation between them is 1 – so they are highly consistent but don’t agree. If using a mean [ICC(#, k)], consistency is typically fine, especially for coding tasks, as mean differences between raters won’t affect subsequent analyses on that data. But if you are interested in determining the reliability for a single individual, you probably want to know how well that score will assess the real value.
Once you know what kind of ICC you want, it’s pretty easy in SPSS. First, create a dataset with columns representing raters (e.g. if you had 8 raters, you’d have 8 columns) and rows representing cases. You’ll need a complete dataset for each variable you are interested in. So if you wanted to assess the reliability for 8 raters on 50 cases across 10 variables being rated, you’d have 10 datasets containing 8 columns and 50 rows (400 cases per dataset, 4000 total points of data).
A special note for those of you using surveys: if you’re interested in the inter-rater reliability of a scale mean, compute ICC on that scale mean – not the individual items. For example, if you have a 10-item unidimensional scale, calculate the scale mean for each of your rater/target combinations first (i.e. one mean score per rater per ratee), and then use that scale mean as the target of your computation of ICC. Don’t worry about the inter-rater reliability of the individual items unless you are doing so as part of a scale development process, i.e. you are assessing scale reliability in a pilot sample in order to cut some items from your final scale, which you will later cross-validate in a second sample.
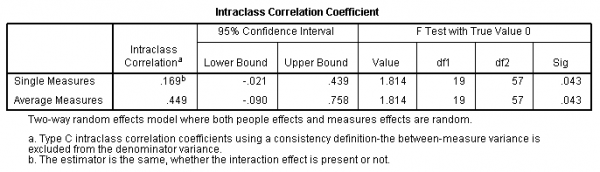
In each dataset, you then need to open the Analyze menu, select Scale, and click on Reliability Analysis. Move all of your rater variables to the right for analysis. Click Statistics and check Intraclass correlation coefficient at the bottom. Specify your model (One-Way Random, Two-Way Random, or Two-Way Mixed) and type (Consistency or Absolute Agreement). Click Continue and OK. You should end up with something like this:
In this example, I computed an ICC(2) with 4 raters across 20 ratees. You can find the ICC(2,1) in the first line – ICC(2,1) = .169. That means ICC(2, k), which in this case is ICC(2, 4) = .449. Therefore, 44.9% of the variance in the mean of these raters is “real”.
So here’s the summary of this whole process:
- Decide which category of ICC you need.
- Determine if you have consistent raters across all ratees (e.g. always 3 raters, and always the same 3 raters). If not, use ICC(1), which is “One-way Random” in SPSS.
- Determine if you have a population of raters. If yes, use ICC(3), which is “Two-Way Mixed” in SPSS.
- If you didn’t use ICC(1) or ICC(3), you need ICC(2), which assumes a sample of raters, and is “Two-Way Random” in SPSS.
- Determine which value you will ultimately use.
- If a single individual, you want ICC(#,1), which is “Single Measure” in SPSS.
- If the mean, you want ICC(#,k), which is “Average Measures” in SPSS.
- Determine which set of values you ultimately want the reliability for.
- If you want to use the subsequent values for other analyses, you probably want to assess consistency.
- If you want to know the reliability of individual scores, you probably want to assess absolute agreement.
- Run the analysis in SPSS.
- Analyze>Scale>Reliability Analysis.
- Select Statistics.
- Check “Intraclass correlation coefficient”.
- Make choices as you decided above.
- Click Continue.
- Click OK.
- Interpret output.
- Shrout, P., & Fleiss, J. (1979). Intraclass correlations: Uses in assessing rater reliability. Psychological Bulletin, 86 (2), 420-428 DOI: 10.1037/0033-2909.86.2.420 [↩]
| Previous Post: | Learn About Our University Library Through Minecraft |
| Next Post: | New Research Links Social Media Marketing and Purchase Intentions |



Thank Dr. Landers. Very informative. Just what I was looking for in my research on ICC and inter-rater reliability.
Glad to help! This has actually become one of my most popular posts, so I think there really was a need here. Just be sure to note that this terminology is the Shrout and Fleiss terminology – for example, some researchers refer to ICC(1,k) as ICC(2), especially in the aggregation/multilevel models literature.
Dear Dr. Landers,
I am currently doing my dissertation for which I have developed a 25-item test that requires explanation from students; hence, a rubric was used for checking . The test was pilot tested to 105 students. My question is: Is it fine to have just two raters, each rater rating all 25 explanations of the 105 students? Or is it necessary that there are at least 3 raters? What type of ICC is appropriate to use and how do I go about it in SPSS?
Thank you so much and more power!
I don’t at all understand what your raters or doing or why from your description, so that makes it difficult to answer this. The number of raters you need is dependent on what you want to do with the scores next. The appropriate type of ICC is dependent on your answers to the various questions in this article above. The process for calculating it is also described above.
Very informative and helpful, well explained and easy to use – thank you
Dr Landers,
This was very helpful. I just have one question for you. In my research I am averaging my raters to develop a new variable; therefore is it correct that the Average Measures ICC is the coefficient I am most interested in?
Yes, if you’re using the average of the ratings you collected in further analyses, the reliability of that variable will be the “average measures” (,k) version.
Thank you so much. I had looked to other informations and have still some doubts. Your explanations are so clear. You really know how to explain to non-statistic people.
Congratulations for your didactic ability.
Sofía
In my case, I have only two raters (a sample) rating many individuals each (around 50), and rating them according to different criteria (for example: accuracy, speed, etc).
According to your explanations, I should apply 2-way random ANOVA with absolute agreement, since I am interested not only in consistency, but also in the reliability of a single rater.
My doubt is if I am able to apply this ICC, or as I only have two raters, if it would be preferable to apply a Pearson correlation.
Thank you very much.
Best wishes,
Sofía
Hello again,
Actually I am trying to validate a assessment rating scale, which evaluates different criteria by observing a subject.
Two observers rated then 50 subjects with this scale.
In order to validate the scale, I should validate each one of its questions (criterion).
I should do an ICC for each one of my criteria, isn’t it?
I guess if Sig < 0.05 for a criteria and if I obtain a high intraclass correlation (what should be considered high? greater than 0.75?) I can deduce that that particular criterion is consistent and reliable, even if I only had two raters?
Am I right?
Thank you very much.
Sofía
ICC only assesses reliability; this is a distinct concept from validation. For a measure to be valid, it must also be reliable, but reliability alone does not guarantee validity. So computing ICC should be only part of a larger validation strategy.
To assess ICC when looking at a scale, compute the scale mean for each rater separately first. Then compute ICC. If you are using the same 2 raters for every person, and you want to assess the reliability of a single rater, you are correct: you need ICC(2,1), which is 2-way Random with Absolute Agreement.
I would not worry about statistical significance testing in this context. A statistically significant ICC just tells you that it’s unlikely that your ICC was drawn from a population where the true ICC was 0. That’s not a very interesting question for what you’re doing. Instead, just see how high ICC is.
The general recommendation by Cohen was that reliability be above 0.7, which means 70% of observed variance is “real” variance. But it really depends on what you’re willing to accept, or what the research literature suggests is typical/necessary. Any non-perfect reliability will decrease the validity of your measure, so it’s mostly a matter of how large you are willing that effect to be.
Thank you very much for your reply.
Then, I understand that I can do ICC with only two raters (they are the same two raters for every person) to test the reliability of my scale.
However, I do not understand why should I do the mean… do you mean:
a) the mean of the ratings of all questions for each person and for each rater
b) the mean of the ratings of a single question given by one rater to all the people
I guess you meaned option a), because otherwise, for option b), if my scale has 13 questions to rate, I should first of all calculate the mean of the answers of rater1 for all those 13 questions, then the mean of rater2. If I do this I would have 13 values for each of the raters, and then, doing the ICC with just two measures (the mean of each rater) I guess it does not make sense?
However, even if you mean option a), wouldn’t that give a reliability of the whole test (composed by 13 questions) but not of every single question?
Can´t I do:
1) the ICC for each question calculating the ICC comparing all the ratings given by each rater to all the people for that particular question.
2) the mean, according to option a) to calculate the ICC of the whole scale.
Thank you very much for your time and for your fast response.
Best wishes
Sorry – I should been clearer. By “scale,” I assumed you meant you have multiple items (questions) assessing the same construct.
You should assess reliability for each distinct measurement concept. So if you had 13 questions that all assessed “happiness,” you should compute ICC on the mean of those items. If you have 13 questions that all assess different things, you should compute 13 ICCs. But I will warn you that ICC tends to be low if you are assessing any psychological constructs with only single items each.
Thank you very much for your reply. Now it is clear.
On the other hand, do you know about any site where I can find a more detailed explanation about how to validate a scale? (not only reliability, but also validity).
Best wishes,
Sofia
Thank you Dr. Landers, this way very helpful!
May I have one question, just to make it clear for myself.
If I have a 15-item interview (with a scale 1-2-3) and 10 raters (population, and always the same 10 raters) rate 5 patients. I am interested in the average reliability of the raters and also I would like to know the reaters’ individual “performance”. This would be a “Two way mixed” in SPSS.
Should I then create a database for each item of the interview (that’d be 15 databases) and run “Two way mixed” and “Absolute agreement”, right? And then computing the mean of the results? Or can I do that I create a database for each patient with 15 rows (items) and 10 columns (raters) and run the Two way mixed?
I guess I am a little bit confused what does “add ,k to the ICC” or “add ,1” mean?
THank you very much for your help!
Best regards
Mark
@Sofia – Validation is a much, much more complicated concept than reliability. I don’t know of any websites that explain it very clearly, although there are entire textbooks devoted to it.
@Mark – Are the 15 questions assessing the same thing? If so, compute a scale mean and then run your statistics on that. You would only look at reliability by item if you were going to use those 15 items individually later. If that’s what you’re going to do, yes, you would need separate SAV files for each database.
,k means you are referring to an ICC of the average ratings. ,1 means you are referring to an ICC of an individual rater. You cannot use ICC to identify the “performance” of any particular rater; instead, all you can tell is the reliability of raters on average or the reliability of a single rater taken at random from your population.
Thank you very much, Richards. Your comments have been of great help. Do you know if there is any statistical forum where to ask doubts online?
Best wishes,
Sofía
Validation isn’t so much statistics as it is a family of research methods. But sure – one statistics forum you might find useful is http://stats.stackexchange.com/
Dear Dr. Landers,
thank you for your answer!
THe 15 item measure the same psychological construct (borderline disorder), but not the same thing, since the items about different symptomps of the disorder – I think this is what you asked. So, later in the research these items will be used (asked) separately and will be evaluated by the raters based on the interview.
So, if I get it right, in this case I’ll need separate SAV files for each item and then compute a mean and that’ll be the overall ICC of the raters.
I can I use ICC for binary data (e.g. 1=borderline, 2=not borderline)? Because we would like to not just compute ICC for the individual items and the overall interview, but we’d like to compute ICC for the final diagnosis (borderline/not borderline).
…and thank you, now I understand what ‘single measure’ means!
Regards, and thank you very much for your kind answers!
Mark Berdi
@Mark – if you are interested in assessing the reliability of symptom ratings, then you need ICCs for each item. If you are interested in assessing inter-rater reliability in general (i.e. the reliability relevant to any future statistics computed using a “borderline score”), you’ll want to compute the scale means for each rater and compute ICC for those means. You should not take an average of ICCs, as that’s not an interpretable value – if you’re interested in the ICC of overall scales, that’s what you should compute the ICC on.
For binary data, you could use ICC, but it is not recommended – I would look into Fleiss’ kappa.
Thank you!
I understood it. I just computed what I needed.
Best regards
Mark Berdi
Hello Dr. Landers,
First, thank you for an excellent resource. We are following your method to conduct interrater reliability. In reference to question 2: sample v. population of raters, what criteria do you use to determine the response?
Additionally, we have found an error will result when raters are in perfect agreement (e.g., all 3 raters assign a score of 2 for a given item). Is this due to the lack of variance and inability to proceed with additional calculations?
Any advice or direction is welcomed.
Sincerely,
Emily and Laura
@Emily & Laura – It just depends on what you want to generalize to. If your raters are the only raters that you ever want to worry about, you have a population. If they are a random sample of such raters, you have a sample. For example, if you have three people watch videos and make ratings from them, the three people you have watching the videos are only three possible raters – you could just as easily have chosen another three drawn from the same population. Therefore, they are a sample of raters.
As for your second question, if your raters are always in perfect agreement, you have no need for ICC. Your reliability is 100% (1.0), so there is nothing to assess.
Thank you for this helpful website. I just want to be clear about question 1. If I have 100 fifteen second clips of children misbehaving and I have a single rater (Sally) rate from 1-7 how bad the misbehavior is for each clip and I have Sam give the same misbehavior ratings to 33 of those clips, it sounds like I have answered “yes” to question 1. Is that right?
And if there is any deviation from this (e.g. I have Bill rate another 33 clips that Sally rated), I answer “no”. Is that also correct?
@Camilo – I’m not sure that I’m clear on your premise, but I will take a stab at it.
If Sally and Sam rate identical clips, then yes – you have “yes” to Q1. However, if you have 2 ratings for 33 clips and only 1 rating for 66 clips, you can only calculate ICC for those 33 clips. If you want to generalize to all the clips (e.g. if you were using all 100 clips in later analyses), you’d need to use the “Single Measure” version of ICC, since you only have 1 rater consistently across all ratees.
If you had Bill rate an additional 33 clips, you’d still have 2 ratings for 66 clips and 1 rating for 33 clips, so nothing has changed, procedurally. However, because you have a larger sample, you’d expect your ICC to be more accurate (smaller confidence interval).
The only way to use the “Average Measures” version of ICC is to have both raters rate all clips (two sets of 100 ratings).
Hi Dr Landers,
This is by far the most helpful post I have read.
I still have a question or two though..
I am looking at the ICC for 4 raters (sample) who have all rated 40 cases.
I therefore think I need the random mixed effects model (ICC, 2,k)
In SPSS i get a qualue for single measures and average measures and I am not sure which i want. My assumption is average measures?
Also i have seen variations in how ICC values are reported and I wondered if you knew the standard APA format, my guess would be [ICC(2, k) = ****].
Any guidance would be very much appreciated.
Many thanks, Anne-Marie.
@Anne-Marie – the “k” indicates that you want Average Measures. Single Measure would be ,1. If you’re using their mean rating in later analyses, you definitely want ,k/Average Measures.
As for reporting, there is no standard way because there are several different sources of information on ICC, and different sources label the different types slightly differently (e.g. in the multilevel modeling literature, ICC(2,1) and ICC(2,k) are sometimes referred to as ICC(1) and ICC(2), respectively, which can be very confusing!).
If you’re using the framework I discuss above, I’d recommend citing the Shrout & Fleiss article, and then reporting it as: ICC(2,4) = ##.
Dr Landers,
Thank you so much!
All calculated and all looking good!
Anne-Marie.
Very useful and easy to understand. I am currently completing my dissertation for my undergraduate physiotherapy degree and stats is all very new. This explained it really easily. Thanks again!
I am training a group of 10 coders, and want to assess whether they are reliable using training data. During training, all 10 code each case, but for the final project, 2 coders will code each case and I will use the average of their scores. So for the final project, I will calculate ICC (1, 2), correct? Then what should I do during training–calculating ICC (1, 10) on the training cases will give me an inflated reliability score, since for the real project it will be only 2 coders, not 10?
@Catherine – It’s important to remember that reliability is situation-specific. So if you’re not using the training codes for any later purpose, you don’t really need to compute their reliability. You would indeed just use ICC(1,2) for your final reliability estimate on your final data. However, if you wanted to get your “best guess” now as to what reliability will be for your final coding, using your training sample to estimate it, you could compute ICC(1,1) on your training sample, then using the Spearman-Brown prophesy formula to identify what the reliability is likely to be with 2 raters. But once you have the actual data in hand, that estimate is useless.
Hello,
I have a small question that builds on the scenario described by Emily & Laura (posted question and answer on March 26, 2012 in regards to the error that results when raters are in perfect agreement).
In my case, only a portion of my 21 raters are in perfect agreement, and so SPSS excludes them from the reliability analyses, resulting in (what I would think to be) an artificially low ICC value, given that only ‘non-agreeing’ raters are being included. Is there a way to deal with this?
Many thanks,
Stephanie
@Stephanie – My immediate reaction would be that ICC may not be appropriate given your data. It depends a bit on how many cases you are looking at, and what your data actually looks at. My first guess is that your data is not really quantitative (interval or ratio level measurement). If it isn’t, you should using some variant of kappa instead of ICC. If it is, but you still have ridiculously high but not perfect agreement, you might simply report percentage agreement.
Dear Dr. Landers,
You are indeed correct – my data are ordered categorical ratings. 21 raters (psychiatrists) scored a violence risk assessment scheme (comprised of 20 risk factors that may be scored as absent, partially present, or present – so a 1,2,3 scale) for 3 hypothetical patients. So I am trying to calculate the reliability across raters for each of the 3 cases.
My inclination was to use weighted kappa but I was under the impression it was only applicable for designs with 2 raters?
Thanks again,
Stephanie
Ahh, yes – that’s the problem then. ICC is not really designed for situations where absolute agreement is common – if you have interval level measurement, the chance that all raters would score exactly “4.1” (for example) is quite low.
That restriction is true for Cohen’s kappa and its closest variants – I recommend you look into Fleiss’ kappa, which can handle more than 2 raters, and does not assume consistency of raters between ratings (i.e. you don’t need the same 3 raters every time).
Thank you
Can you explain to me the importance of upper and lower Bound (CI 95%)?. “How to take advantage of” CI?
That’s not really a question related to ICC. If you are looking for general help on confidence intervals, this page might help: http://stattrek.com/estimation/confidence-interval.aspx
Thank you for this clear explanation of ICCs. I was wondering if you might know about them in relation to estimate intrarater reliability as well? It seems as if the kappa may provide a biased estimate for ordinal data and the ICC may be a better choice. Specifically, I’m interested in the intrarater reliability of 4 raters’ rating of an ordinal 4 point clinical scale that evaluates kidney disease, each rater rated each patient 2 times.
I’m using SAS and can’t seem to get the ICC macro I used for interrater reliabilty to work. I’m wondering if the data need to be structured with rater as variables (as you say above)? If so, do you know if I would include the two measurements for each patient in a single observation or if I should make two observations per patient?
Thank you-
Lisa
I don’t use SAS (only R and SPSS), so I’m afraid I don’t know how you’d do it there. But I don’t think I’d do what you’re suggesting in general unless I had reason to believe that patients would not change at all over time. If there is true temporal variance (i.e. if scores change over time), reliability computed with a temporal dimension won’t be meaningful. ICC is designed to assess inter-rater consistency in assessing ratees controlling for intra-rater effects. If you wanted to know the opposite (intra-rater consistency in assessing ratees controlling for inter-rater effects), I suppose you could just flip the matrix? I am honestly not sure, as I’ve never needed to do that before.
Thanks for yuor thoughts.
Hello Richard,
Thanks a lot for your post. I have one question: I built an on-line survey that was answered by 200 participants. I want to know if the participants did not show much variance in their answers so to know that the ratings are reliable. For that matter, I am running a One-way random effects model and then I am looking at the average measures.
That’s the way I put it:
Inter-rater reliability (one-way random effects model of ICC) was computed using SPSS (v.17.0). One-way random effects model was used instead of Two-way random effects model because the judges are conceived as being a random selection of possible judges, who rate all targets of interest. The average measures means of the ICC was 0.925 (p= 0.000) which indicates a high inter-rater reliability therefore reassuring the validity of these results (low variance in the answers within the 200 participants).
I would be happy if you could tell me whether a one-way random effects model of ICC and then looking at the average measures is the way to go.
Thank you,
John
@John – Your study is confusing to me. Did you have all 200 participants rate the same subject, and now you are trying to determine the reliability of the mean of those 200 participants? If so, then you have done the correct procedure, although you incorrectly label it “validity.” However, I suspect that is not what you actually wanted to do, since this implies that your sample is n = 1. If you are trying to assess variance of a single variable across 200 cases, you should just calculate the variance and report that number. You could also compute margin of error, if you want to give a sense of the precision of your estimate. If you just want to show “variance is low,” there is no inferential test to do that, at least in classical test theory.
Thank you for your answer, Richard.
I built an on-line survey with a 100 items.
Subjects used a 5 point Lickert scale to indicate how easy was to draw those items.
200 subjects answered the on-line survey.
I want to prove the validity of the results. If the ICC cannot be used for that matter. Can I use the Cronbach’s alpha?
Thanks for your time.
Best,
John
@John – Well, “reliability” and “validity” are very different concepts. Reliability is a mathematical concept related to consistency of measurement. Validity is a theoretical concept related to how well your survey items represent what you intend them to represent.
If you are trying to produce reliability evidence, and you want to indicate that all 100 of your items measure the same construct, then you can compute Cronbach’s alpha on those items. If you have subsets of your scale that measure the same construct (at least 2 items each), you can compute Cronbach’s alpha for each. If you just asked 100 different questions to assess 100 different concepts, alpha isn’t appropriate.
If your 100 items are all rating targets theoretically randomly sampled from all possible rating targets, and you had all 100 subjects rate each one, you could calculate ICC(2). But the measure count depends on what you wanted to do with those numbers. If you wanted to compute the mean for each of the 100 rating subjects and use that in other analyses, you’d want ICC(2, 200). If you just wanted to conclude “if one person rates one of these, how reliable will that person’s ratings be?”, then you want ICC(2, 1).
Thank you for your answer, Richard.
I will use Chronbach’s alpha for internal consistency. That way I can say that my survey measured the same general construct: the imageability of the words.
I will use ICC (2,1)(two-way random, average measures) for inter-rater reliability. That way I can say if the subjects answered similarly.
#I am interested in the mean of each item to enter the data in a regression analysis (stepwise method). I am interested then in saying that a word like ‘apple’ has a mean imageability of 2 out of 5. I am not interested in the mean of the answers of each subject. That is, subject 1 answered 3 out of 5 all the the time.
#After running those two statistics, is it OK to talk about validity?
Thanks again.
Best,
John
You can certainly *talk* about validity as much as you want. But the evidence that you are presenting here doesn’t really speak to validity. Statistically, the only thing you can use for this purpose is convergent or discriminant validity evidence, which you don’t seem to have. There are also many conceptual aspects of validity that can’t be readily measured. For example, if you were interested in the “imageability” of the words, I could argue that you aren’t really capturing anything about the words, but rather about the people you happened to survey. I could argue that the 200 pictures you chose are not representative of all possible pictures, so you have biased your findings toward aspects of those 200 pictures (and not a general property of all pictures). I could argue that there are cultural and language differences that change how people interpret pictures, so imageability is not a meaningful concept anyway, unless it is part of a model that controls for culture. I could argue that color is really the defining component, and because you didn’t measure perceptions of color, your imageability measure is meaningless. I suggest reading Shadish, Cook, and Campbell (2002) for a review of validation.
But one key is to remember: a measure can be reliable and valid, reliable and invalid, or unreliable and invalid. Reliability does not ensure validity; it is only a necessary prerequisite.
Thank you for the note on validity,Richard.
Please let me know if the use I give to the Chronbach’s alpha for internal consistency and the ICC (2,1)(two-way random, average measures) for inter-rater reliability is reasonable. Those are eery statistics for me, hence, it is important for me to know your take on it.
About the imageability ratings. We gave 100 words to 200 subjects. The subjects told us in a 5 point scale how did they think the words can be put on a picture.
Thanks again.
Best,
John
ICC(2,1) is two-way random, single measure. ICC(2,100) would be your two-way random, average measures. Everything you list is potentially a reasonable thing to do, but it really depends on what you want to ultimately do with resulting values, in the context of your overall research design and specific research questions. I would at this point recommend you bring a local methods specialist onto your project – they will be able to help you much more than I can from afar.
Thank you for your answer, John.
I will try to ask a local methods specialist. So far, the people around me are pretty rusty when it comes to helping me out with all this business.
Thanks again.
Best,
John
Hello Richard,
Thank you for the wonderfull post, it helped very much!
I have a question aswell, if you can still answer, since it’s been a while since anyone posted here.
I have a survey with 28 items, rated 1 -7, by 6 people. I need to know how much agreement is between the 6 on this rating and if possible the items that reach the highest rating (that persons agree most on). It’s a survey with values (single worded items) and I have to do an aggregate from these 6 people’s rating, if they agree on the items, so I can later compare it with the ratings of a larger dataset of 100 people. Let us say that the 6 raters must be have high reliability because they are the ones to optimaly represent the construct for this sample of 105 (people including the raters).
Basicaly: 1.I need to do an aggregate of 6 people’s ratings (that’s why I need to calculate the ICC), compare the aggregate of the rest of the sample with this “prototype”, see if they correlate.
2. Determine the items with largest agreement.
What I don’t understand is if I use the items as cases and run an ICC analysis, two way mixed and than look at the single or average?
Hope this isn’t very confusing and you can help me with some advice.
Thank you,
Andra
@Andra – It really depends on which analysis you’re doing afterward. It sounds like you’re comparing a population of 6 to a sample of 99. If you’re comparing means of those two groups (i.e. you using the means in subsequent analyses), you need the reliability of the average rating.
Dear Richard,
Thank you for your answer. I think though that I’ve omitted something that isn’t quite clear to me: the data set in spss will be transposed, meaning I will have my raters on columns and my variables on rows? Also in the post you say to make a dataset for every variable but in this case my variables are my “cases” so I assume I will have only a database with 9 people and 28 variables on rows and compute the ICC from this?
I have yet another question, hope you can help me. What I have to do here is to make a profile similarity index as a measure of fit between some firm’s values as rated by the 9 people and the personal values of the rest of the people, measured on the same variables. From what I understand this can be done through score differences or correlations between profiles. Does this mean that I will have to substract the answers of every individual from the average firm score or that I’ll have to correlate each participant’s scores with that of the firm and then have a new variable that would be a measure of the correlation beween the profiles? Is there any formula that I can use to do this; I have the formula for difference scores and correlation but unfortunatelly my quite moderate mathematical formation doesn’t help ..
I sincerelly hope that this isn’t far beyond the scope of your post and you can provide your expertize for this!
Appreciatively,
Andra
@Andra – It does not sound like you have raters at all. ICC is used in situations like this: 6 people create scores for 10 targets across 6 variables. You then compute 6 ICCs to assess how well the 6 people created scores for each of the 10 targets. It sounds like you may just want a standard deviation (i.e. spread of scores on a single variable), which has nothing to do with reliability. But it is difficult to tell from your post alone.
For the rest of your question, it sounds like you need a more complete statistical consult than I can really provide here. It depends on the specific index you want, the purpose you want to apply it toward, further uses of those numbers, etc. There are many statisticians with reasonable consulting rates; good luck!
Okay Richard, I understand, then I can’t use the ICC in this case. Thought I could because at least one author in a similar paper used it … something like this (same questionnaire, different scoring, theirs had q sort mine is lickert):
“As such, the firm informant’s Q Sorts were averaged, item by
item, for each [] dimension representing each firm.Using James’ (1982) formula, intra-class correlation coefficients (ICCs) were calculated for ascertaining the
member consensus on each dimension. ICC was calculated by using the following formula[]”
Maybe the rWG would be better?
Anyhow, thank you very much for trying to answer, I will re-search the online better for some answers 🙂
All the best,
Andra
Hi Richard,
I just wanted to check something.
If i have 28 cases, and 2 raters rating each case, from a wider population of raters, I think I need…
Two-way Random effects model
ICC 2, 2. for absolute agreement.
When I get the output, do I then report the average measures ICC value, rather than the single measures, as I want to identify the difference between raters?
Many thanks, Anne-Marie.
@Anne-Marie – Reliability doesn’t exactly assess “the difference between raters.” You are instead capturing the proportion of “true” variance in observed score variance. If you intend to use your mean in some later analysis, you are correct. If you are just trying to figure out how consistently raters make their ratings, you probably want ICC(2,1).
Hi Richard, I want to calculate ICC(1) and ICC(2) for the purpose of aggregating individual scores into group level scores. Would the process be similar to what you described for inter-rater reliability.
I would imagine that in the case the group would be equivalent to the rater. That is, instead of looking within rater versus between rater variance, I want within group versus between group variance? Therefore would I just put the grouping IDs along the columns (rather than rater) and the score for each group member along the row?
However, I have varying group sizes, so some groups have 2 member and some have as many as 20. It seems like that could get quite messy… Maybe there is some other procedure that is more appropriate for this?
Dear Richard
thank you, this makes things much clearer concerning how to choose the appropriate ICC.
Can I ask if you have any paper examples on how to report ICCs?
Thank you for your time
Best wishes
Laura
Dear Dr. Landers,
Thank you very much for the information on this forum!
Unfortunately, after studying all the responses on this forum I still have a question:
In total I have 292 cases from which 13 items were rated on a 4-point rating scale. Coder 1 has rated 144 cased, Coder 2 has rated 138 cases and 10 cases were treated as training cases. Three items were combined in a composite score and this score will be used in future studies. So in future studies I want to report this composite score on all 292 cases.
The question now is of course: “What is the intercoder reliability between Coder 1 and Coder 2 on the composite score?” To assess reliability between the coders I want to compare the composite score of both Coders on 35 cases (these were scored by both Coder 1 and Coder 2).
I think I have to use the ICC (2) and measure absolute agreement. Is this correct?
My doubt is if I have to look at the ‘single measure’ or ‘average measure’ in SPSS?
I hope you can help me. Many thanks in advance.
Janneke
@Gabriel – You can use ICC as part of the procedure to assess if aggregation is a good idea, but you can’t do this if group sizes vary substantially. I believe in this case, you want to use within-groups r, but I’m not sure – I don’t do much research of this type.
@Laura – Any paper that reports an ICC in your field/target journal would provide a great example. This varies a bit by field though – even ANOVA is presented different across fields.
@Janneke – You should use “absolute agreement” and “single measure.” Single measure because you’re using ratings made by only one person in future analyses. If you had both raters rate all of them, and then used the mean, you would use “average measure.”
Dear Dr. Landers,
Thank you very much for your quick and clear answer.
Best regards, Janneke
Dear Dr. Landers,
Thank you for such wonderful article. I am sure it is very beneficial to many people out there who are struggling.
I am trying to study the test-retest reliability of my questionnaire (HIV/AIDS KAP survey).
The exact same set of respondents completed the same questionnaire after a 3-week interval. Though anonymous, for the same respondent, I can link both tests at time1 and time2.
Through a lot a of researching, literatures suggest Kappa coefficients for categorical variables and ICC for continuous variables (please comment if I get that wrong).
However, I am still uncertain regarding the model of ICC in SPSS that I should use for my study.
The bottom line conclusion that I would like to make is that the questionnaire is reliable with acceptable ICC and Kappa coefficients.
I would really appreciate your suggestion.
Thank you very very much.
Teeranee
@Teeranee – Neither ICC nor Kappa are necessarily appropriate to assess test-retest reliability. These are both more typically estimates of inter-rater reliability. If you don’t have raters and ratees, you don’t need either. If you have a multi-item questionnaire, and you don’t expect scores to vary at the construct level between time points, I would suggest the coefficient of equivalence and stability (CES). If you’re only interested in test re-test reliability (e.g. if you are using a single-item measure), I’d suggest just using a Pearson’s correlation. And if you are having two and only two raters make all ratings of targets, you would probably use ICC(2).
Dr. Landers,
Thank you very much for your reply.
I will look into CES as you have suggested.
Thank you.
Dear Dr. Landers,
Many thanks for your summary, it very, very helpful. I wanted to ask you one more question, trying to apply the information to my own research. I have 100 tapes that need to be rated by 5 or 10 raters and I am trying to set pairs of raters such that each rater codes as few tapes as possible but I am still able to calculate ICC. The purpose of this is to calculate inter-rater reliability for a newly developed scale.
Thank you very much.
@Violeta – I’m not sure what your question is. Reliability is a property of the measure-by-rater interaction, not the measure. For example, reliability of a personality scale is defined by both the item content and the particular sample you choose to assess it (while there is a “population” reliability for a particular scale given a particular assessee population, there’s no way to assess that with a single study or even a handful of studies). Scales themselves don’t have reliability (i.e. “What is the reliability of this scale?” is an invalid question; instead, you want to know “What was the reliability of this scale as it was used in this study?”). But if I were in your situation (insofar as I understand it), I would probably assign all 10 raters to do a handful of tapes (maybe 20), then calculate ICC(1,k) given that group, then use the Spearman-Brown prophecy formula to determine the minimum number of raters you want for acceptable reliability of your rater means. Then rate the remainder with that number of raters (randomly selected for each tape from the larger group). Of course, if they were making ratings on several dimensions, this would be much more complicated.
Dear Dr. Landers,
Thank you very much for your clarifications and for extracting the question from my confused message. Thank you very much for the solution you mentioned, it makes a lot of sense, and the main impediment to applying it in my project is practical – raters cannot rate more than 20 tapes each for financial and time reasons. I was thinking of the following 2 scenarios: 1) create 10 pairs of raters, by randomly pairing the 10 raters such that each rater is paired with 2 others; divide the tapes in blocks of 10 and have each pair of raters code a block of 10 tapes; in the end I would calculate ICC for each of the 10 pairs of raters, using ICC(1) (e.g., ICC for raters 1 and 2 based on 10 tapes; ICC for raters 1 and 7 based on 10 tapes, etc.); OR, 2) create 5 pairs of raters, by randomly pairing the 5 raters such that is rater is paired with one other rater; divide the tapes in blocks of 20 and have each pair of raters code a block of 20 tapes; I would end up with 5 ICC(1) (e.g., ICC for raters 1 and 5 based on 20 tapes, etc.). Please let me know if these procedures make sense and if yes, which one is preferrable. Thank you very much for your time and patience with this, it is my first time using this procedure and I am struggling a bit with it. I am very grateful for your help.
You need ICC(1) no matter what with different raters across tapes. It sounds like you only want 2 raters no matter what reliability they will produce, in which case you will be eventually computing ICC(1,2), assuming you want to use the mean rating (from the two raters) in subsequent analyses. If you want to assess how well someone else would be able to use this scale, you want ICC(1,1).
As for your specific approaches, I would not recommend keeping consistent pairs of raters. If you have any rater-specific variance contaminating your ratings, that approach will maximize the negative effect. Instead, I’d use a random pair of raters for each tape. But I may not be understanding your approaches.
Also, note that you’ll only have a single ICC for each type of rating; you don’t compute ICC by rater. So if you are having each rater make 1 rating on each tape, you’ll only have 1 ICC for the entire dataset. If you are having each rater make 3 ratings, you’ll have 3 ICCs (one for each item rated). If you are having each rater make 3 ratings on each tape but then take the mean of those 3 ratings, you’ll still have 1 ICC (reliability of the scale mean).
Thank you very much, this is so helpful! I think that it is extraordinary that you take some of your time to help answering questions from people that you don’t know. Thank you for your generosity, I am very grateful!
Dear Richard,
I have two questions:
– Can you use the ICC if just one case (person) is rated by 8 raters on several factors (personality dimensions)? So not multiple cases but just one.
– Can you use ICC when the original items (which lead to a mean per dimension) are ordinal (rated on a 1-5 scale)? So can I treat the means of ordinal items as continues or do I need another measure of interrater reliability?
I hope you can help me!
1) No; ICC (like all reliability estimates) tells you what proportion of the observed variance is “true” variance. ICC’s specific purpose is to “partial out” rater-contributed variance and ratee-contributed variance to determine the variance of the scale (given this measurement context). If you only have 1 case, there is no variance to explain.
2) ICC is for interval or higher level measurement only. However, in many fields in the social sciences, Likert-type scales are considered “good enough” to be treated as interval. So the answer to your question is “maybe” – I’d recommend consulting your research literature to see if this is common.
Dr. Landers,
In your response to Gabriel on 8/15/12, you indicated that ICC(1) is appropriate for ratings made by people arranged in teams when the teams vary in size (i.e., number of members). However, a reviewer is asking for ICC (2) for my project where my teams also vary in size. How would you respond?
Many kind thanks!
Looking back at that post, I actually don’t see where I recommended that – I was talking about ICC in general. As I mentioned then, the idea of aggregation in the teams literature is more complex than aggregation as used for coding. For an answer to your question, I’d suggest taking a look at:
Bliese, P. (2000). Within-group agreement, non-independence, and reliability. In K. Klein and S. Kozlowski (Eds), Multilevel theory, research, and methods in organizations. San Francisco: Jossey-Bass (pp. 349-381).
Hofmann, D. A. (2002). Issues in multilevel research: Theory development, measurement; and analysis. In S. Rogelberg (Ed.), Handbook of Research Methods in Industrial and Organizational Psychology. Malden, MA: Blackwell.
Klein, K. l, Dansereau, F., and Hall, Rl (1994). Levels issues in theory development, data collection, and analysis. Academy of Management Review, 19, 195-229.
Thank you! Bliese (2000) was particularly helpful.
Dr. Landers,
Regarding consistency across raters – I have an instrument with more items (30) and 100 persons rating the items. If I analyse the internal consistency of the scale in SPSS and choose the ICC two way random option, can I use the result for the ICC as indicating level of consistency on scale items across my 100 raters? Is that correct or are there other calculations I must perform? I need to know if the ratings of the items are consistent to form an aggregate.
Thank you, hopefully you can provide some advice!
I don’t think you’re using the word “rating” in the methodological sense that it is typically used related to ICC. By saying you have 100 persons rating the items, you imply that those are not the “subjects” of your analysis. Based on what you’re saying, you have 100 _subjects_, which are each assessed with 30 items (i.e. 3000 data points). If so, you probably want coefficient alpha (assuming your scale is interval or ratio level measurement).
Dr Landers,
Thank you for the answer. Perhaps I did not express the issue properly. The 30 items refer to an “individual” (in a way put, or a larger entity, an organization) so the respondents would be assessing someone else on the 30 items, not self-rating themselves.Could I use the ICC as mentioned, by choosing the option from reliability analysis in SPSS in this case, or similarly, more calculations need to be performed?
Anxiously waiting for a response …
It depends. How many people are being assessed by the raters, and a related question, how many total data points do you have? Are the 100 raters scoring the 30 items for 2 others, 3 others, etc?
For example, it’s a very different problem if you have 100 raters making ratings on 50 subjects, each making 2 sets of ratings on 30 items (a total of 3000 data), versus 100 raters making ratings on 100 subjects, each making 1 rating on 30 items (also a total of 3000 data).
If you have 100 raters making ratings on 100 subjects (1 set of 30 ratings each), you have perfectly confounded raters and subjects, and there is no way to determine the variance contributed by raters (i.e. ICC is not applicable). If you have more than 1 rating for each subject, yes – you can calculate ICC for each of your 30 items, or if it’s a single scale, you can calculate scale scores and compute a single ICC on that. If you want to treat the items on the scale as your raters, that’s also a valid reliability statistic, but it still doesn’t assess any inter-rater component.
Hi Dr. Landers..
I came across this useful information as I was searching about ICC.
Thank you for this information explained in a clear way.
I have a question, though.
If, I have 5 raters marking 20 sets of essays. First, each raters will mark the same 20 essays using analytic rubric. Then, after an interval of 2 weeks, they will be given the same 20 essays to be marked with different rubric, holistic rubric. The cycle will then repeated after 2 weeks (after the essays collected from Phase 2), with the same 20 essays & analytic rubric. Finally after another 2 weeks, the same 20 essays and holistic rubric. Meaning, for each type of rubric, the process of rating/marking the essays will be repeated twice for interval of 1 month.
Now, if I am going to look for inter rater reliability among these 5 raters and there are 2 different rubrics used, which category of ICC should I use? Do I need to calculate it differently for each rubric?
If I am looking for inter rater reliability, I don’t need to do the test-retest method & I can just ask the raters to mark the essays once for each type of rubric, and use ICC, am I right?
And can you help me on how I should compute intra rater reliability?
Thank you in advance for you response.
Regards,
Eme
It depends on how you are collecting ratings and what you’re going to do with them. I’m going to assume you’re planning on using the means on these rubrics at each of these stages for further analysis. In that case, for example:
1) If each rater is rating 4 essays (i.e. each essay is rated once), you cannot compute ICC.
2) If each rater is rating 8 essays (i.e. each essay is rated twice), you would compute ICC(1,2).
3) If each rater is rating 12 essays (i.e. each essay is rated thrice), you would compute ICC(1,3).
4) If each rater is rating 16 essays (i.e. each essay is rated four times), you would compute ICC(1,4).
5) If each rater is rating 20 essays (i.e. each essay is rated by all 5 raters) you would compute ICC(2,5)
You’ll need a separate ICC for each time point and for each scale (rubric, in your case).
Intra-rater reliability can be assessed many ways, depending on what your data look like. If your rubric has multiple dimensions that are aggregated into a single scale score, you might use coefficient alpha. If each rubric produces a single score (for example, a value from 0 to 100), I’d suggest test re-test on a subset of essays identical (or meaningfully parallel) to these. Given what you’ve described, that would probably require more data collection.
‘Thank you, Dr Landers, I think it makes sense now. Basically the 30 items make a scale. My 100 raters rate one individual (the organization in which they work, which is the same for all of them) on these 30 items or the scale. So 100 people rate, each of them, every item in the scale once for a rated “entity”. Then, at least if I have understood it correctly, I can report the ICC for the scale and use it as argument for aggregation. Hope I make more sense now .. Please correct me if it is still not a proper interpretation.
It sounds like you have one person making one rating on one organization. You then have 100 cases each reflecting this arrangement. This still sounds like a situation better suited to coefficient alpha, since you are really assessing the internal consistency of the scale, although ICC(2,k) should give you a similar value. You cannot assess the reliability of the raters (i.e. inter-rater reliability0 in this situation – it is literally impossible, since you don’t have repeated measurement between raters.
If by aggregation, you mean “can I meaningfully compute a scale mean among these 30 items?”, note that a high reliability coefficient in this context does not alone justify such aggregation. In fact, because you have 30 items, the risk of falsely concluding the presence of a single factor based upon a high reliability coefficient is especially high. See http://psychweb.psy.umt.edu/denis/datadecision/front/cortina_alpha.pdf for discussion of this concept.
Dr. Landers,
I am trying to determine reliability of portfolio evaluation with 2 raters examining the same portfolios with an approximate 40-item Likert (1-4) portfolio evaluation instrument.
Question 1: If I am looking for a power of .95, how can I compute the minimum number of portfolios that must be evaluated? What other information do I need?
Question 2: After perusing your blog, I think I need to use ICC (3) (Two-way mixed) because the same 2 raters will rate all of the portfolios. I think I am interested in the mean rating, and I think I need a measure of consistency. Am I on the right track?
I appreciate your time and willingness to help all of us who are lost in Statistics-World.
Cindy
For Q1, I assume you mean you want a power of .95 for a particular statistical test you plan to run on the mean of your two raters. This can vary a lot depending on the test you want to run and what your other variable(s) looks like. I suggest downloading G*Power and exploring what it asks for: http://www.psycho.uni-duesseldorf.de/aap/projects/gpower/
For Q2, are your two raters the only two people that could ever conceivably rate these portfolios? If so, you are correct – ICC(3,2), consistency. If not (for example, if other people trained equally well as these two could do the same job), you probably want ICC(2,2), consistency. ICC(3) is very uncommon, so unless you have a compelling reason to define your two raters as a complete population of raters, I’d stick with ICC(2).
Hi,
This post was very helpful – thank you for putting the information together.
Any thoughts on sample size? If I would like to estimate interrater reliability for various items on a measure, any thoughts on how many cases I should have for each item?
For instance, if I want to know if social workers can provide a reliable measure of impulsitivity (one-item Q on an assessment form with 3 ordinal response options) when first meeting a child, how many reports of impulsivity (N= how many children?) would I need for this to be an accurate determination of interrater reliability?
And is there a suggested sample size of social workers?
Thank you –
I think your conceptualization of reliability may not be quite right. Reliability is itself a function of the raters and the situation they are in – in other words, you don’t check “if” social workers can provide a reliable measure, but instead you have them make ratings and check to see how reliable _they were_. So sample size/power isn’t really an issue – if you have fewer ratings, they will be less reliable. If you have more ratings, they will be more reliable. A reliability question would be, “how many social workers do I need to reliably measure impulsivity given this set of children?” But if you’re interested in determining the reliability of a single social worker as accurately as possible (i.e. minimizing the width of the confidence interval around ICC) to determine how accurate a social worker drawn from your population of social workers might be when making a judgment on their own, that is a different question entirely.
Thank you for getting back to me so quickly.
Yes, you’re right. I wasn’t conceptualizing this accurately. And you’re also right in speculating that I want to know how reliable a single social worker would be when asked to make a judgement on their own, using the provided scale.
After looking more closely at previous posts, it seems I have a situation similar to Stephanie that will require me to use Fleiss’ kappa?
It depends on what your scale looks like. If they are making ratings on an interval- or ratio-level scale, you can (and should) still use ICC. Kappa is for categorical ratings. You would also need to use the Spearman-Brown prophecy formula to convert your kappa to reflect the reliability of a single rater, whereas with ICC, you can just look at ICC(#, 1).
Dr. Landers,
Although there have already been asked so many questions, I still have one. Hopefully you can help me out (because I am totally lost).
I have done a prétest with 36 advertisements. Every advertisement can be categorized in one of the 6 categories. 15 People have watched all the 36 advertisements and placed each advertisement individually in one of the six categories (So for example: Ad1 – Cat. A; Ad2 – Cat D; Ad1 – Cat B, etc). They also have rated how much they liked the advertisement (from 1 – 5).
In my final survey I want to use one or two advertisements per category. But to find out which advertisement belongs in what category I have done the pretest (so which advertisement is best identified as the advertisement that belongs in thát category) (I want to measure the effects of the different category advertisements on people). The advertisements with the highest ratings (that the raters placed the most often in that category) will be used.
My mentor says I have to use inter-rater reliability. But I feel that Cohen’s Kappa is not usable in this case (because of the 15 raters). But I have no idea how or which test I háve to use.
Hopefully you understand my question and hopefully you can help me out!
Best regards,
Judith
This is not really an ICC question, but I might be able to help. Your mentor is correct; you need to assess the reliability of your ratings. 15 raters is indeed a problem for Cohen’s kappa because it limits you to two raters; you should use Fleiss’ kappa instead – at least for the categorical ratings. You could use ICC for the likability ratings.
Thank you for your quick answer!
However, I use SPSS but the syntax I found online are not working properly (I get only errors). Is there some other way in SPSS (20.0) to calculate Fleiss?
Thank you!
Thank you, Dr. Landers!
Dear Dr Landers,
I’m an orthopaedician trying to assess if three observers measuring the same 20 different bones ( length of the bone) using the same set of calipers and the same method have a large difference when they measure it. I’ve calculated the ICC for intra-observer variation using intraclass 2 way mixed(ssps 16). Do I have to calculate three different ICC’s or can I get all three sets of data together and get a single ICC for all of us? We’ve measured the 20 different bones and the raters were the same. The variables were continuous in mm. And if i cant use ICC what should I use instead to measure inter observer variation between 3 observers?
Another small doubt- during the process of reading about this I chanced upon this article suggesting CIV or coefficient of inter observer variability-
Journal of Data Science 3(2005), 69-83, Observer Variability: A New Approach in Evaluating
Interobserver Agreement , Michael Haber1, Huiman X. Barnhart2, Jingli Song3 and James Gruden
Now do I need to use this as well?
I was referred here by another website that I was reading for information about ICC- 1) i really appreciate that you’ve taken time out to reply to all the questions, and 2)very lucidly explained ( ok, ok, admit I didn’t get the stuff about k and c etc but that’s probably because I m an archetypal orthopod.
regards,
Mathew.
ICC is across raters, so you’ll only have one ICC for each variable measured. So if length of bone is your outcome measure, and it’s measured by 3 people, you’ll have 1 ICC for “length of bone.” ICC also doesn’t assess inter-observer variation – rather the opposite – inter-observer consistency.
There are different standards between fields, so your field may prefer CIV as a measure of inter-rater reliability (I am not familiar with CIV). I can’t really speak to which you should use, as your field is very different from mine! But normally you would not need multiple measures of reliability. I doubt you need both – probably one or the other.
Dear Dr. Landers,
I wanted to know, whether my raters agree with each other and whether anyone of my 10 raters rated so differently, that I have to exclude him. Is the ICC the right measure for that? And is it in my case better to look at the single measures or the average measures?
Regards,
Martina
There isn’t anything built into ICC functions in SPSS to check what ICC would be if you removed a rater; however, it would probably be easiest just to look at a correlation matrix with raters as variables (and potentially conduct an exploratory factor analysis). However, if you believe one of your raters is unlike the others, ensure you have a good argument to remove that person – you theoretically chose these raters because they come from a population of raters meaningful to you, so any variation from that may represent variation within the population which would not be reasonable to remove.
For single vs. average measure, it depends on what you want to do with your ratings. But if you’re using the mean ratings for some other purpose (most common), you want average measures.
Thank you very much for your answer!
Regards,
Martina
Dear Dr. Landers,
Thanks very much. I stuck with ICC.
regards,
Mathew
Dr. Landers,
I have individuals in a team who respond to 3 scale items (associated with a single construct). I would like to aggregate the data to team level (as I have team performance data). How do I calculate the ICC(1) and ICC(2) to justify aggregation? Each of the teams have varying size.
As I mentioned before in an earlier comment, the idea of aggregation in the teams literature is more complex than aggregation as used for coding. For an answer to your question, I’d suggest taking a look at:
Bliese, P. (2000). Within-group agreement, non-independence, and reliability. In K. Klein and S. Kozlowski (Eds), Multilevel theory, research, and methods in organizations. San Francisco: Jossey-Bass (pp. 349-381).
Hofmann, D. A. (2002). Issues in multilevel research: Theory development, measurement; and analysis. In S. Rogelberg (Ed.), Handbook of Research Methods in Industrial and Organizational Psychology. Malden, MA: Blackwell.
Klein, K. l, Dansereau, F., and Hall, Rl (1994). Levels issues in theory development, data collection, and analysis. Academy of Management Review, 19, 195-229.
Dear Dr. Landers,
Your explanation is very helpful to non-statisticians. I have a question. I am doing a test-retest reliability study with only one rater, i.e. the same rater rated the test and retest occasions. Can you suggest which ICC I should use?
Thanks for your advice in advance!
Unfortunately, it’s impossible to calculate inter-rater reliability with only one rater. Even if you want to know the inter-rater reliability of a single rater, you need at least 2 raters to determine that value. If you just want an estimate of reliability, you can use test-retest reliability (a correlation between scores at time 1 and time 2), but it will by definition assume that there is no error in your rater’s judgments (which may or may not be a safe assumption).
Dear Dr. Landers,
I just wanted to express my appreciation for your “labor of love” on this site. Your willingness to provide help (with great patience!) to others struggling with reliability is much appreciated.
From a fellow psychologist…
Jason King
Dear Dr. Landers,
I will be grateful if you can spare some time to answer this.
I am translating an English instrument to measure medication regimen complexity in Arabic. The instrument has three sections and helps to calculate the complexity of medication regimen. I have selected around 10 regimen of various difficulty/complexity for this purpose and plan to use a sample of healthcare professionals such as pharmacists, doctors and nurses to rate them as per the instrument. How do I calculate the minimum number of regimen (though I have selected 10 but can select more) and raters (health care professionals) if I want to test the Inter-rater reliability?
I am not sure I completely understand your measurement situation. It sounds like you want to assess the inter-rater reliability of your translated measure, but I am not sure to what purpose. Are you planning on using this in a validation study? Are you trying to estimate the regimen complexity parameters for your ten regimens? An instrument does not itself have “reliability” – reliability in classical test theory is the product of the instrument by measurement context interaction. So it is not valuable to compute reliability in a vacuum – you only want to know reliability to ultimately determine how much unreliability affects the means, SDs, etc, that you need from that instrument.
Thank you for the comments Dr. Landers,
I want to use the instrument in a validation study to demonstrate the Arabic translation is valid and reliable. For validity, I will be running correlations with the actual number of medications to see if the scale has criterion related validity (increase in number of medications should go hand in hand with increase in complexity scores) and for reliability measurement I was thinking of performing ICC.
Thanks,
Tabish
That is my point – the way you are phrasing your question leads me to believe you don’t understand what reliability is. It is a nonsense statement to say “I want to demonstrate this instrument is reliable” in the context of a single validation study. A particular measure is neither reliable nor unreliable; reliability is only relevant within a particular measurement context, and it is always a matter of degree. If you’re interested in determining how unreliability affects your criterion-related validity estimates in a validation study, you can certainly use ICC to do so. Based upon your description, it sounds like you’d want ICC(1,k) for that purpose. But if you’re asking how many regimen/raters you need, it must be for some specific purpose – for example, if you want a certain amount of precision in your confidence intervals. That is a power question, and you’ll need to calculate statistical power for your specific question to determine that, using a program like G*Power.
Dear Dr Landers
Thank you vefry much for the clear explanation of ICC on your website. There is only one step I do not understand.
We have developed a neighbourhood assessment tool to determine the quality of the neighbourhood environment. We had a pool of 10 raters doing the rating of about 300 neighbourhoods. Each neighbourhood was always rated by two raters. However, there were different combinations (or pairs) of raters for the different neighbourhoods.
This appears a one-way random situation: 600 (2×300) ratings need to be made, which are distributed across the 10 raters (so each rater rated about 60 neighbourhoods).
We now have an SPSS dataset of 300 rows of neighbourhoods by 10 columns of raters. It is however not a *complete* dataset, in the sense that each rater did not rate about 240 (=300-60) neighbourhoods.
I am not sure how we should calculate the ICC here/ or perhaps should input the data differently
Most grateful for your help
ICC can only be used with a consistent number of raters for all cases. Based on your description, it seems like you just need to restructure your data. In SPSS, you should have 2 columns of data, each containing 1 rating (the order doesn’t matter), with 300 rows (1 containing each neighborhood). You’ll then want to calculate ICC(1,2), assuming you want to use the mean of your two raters for each neighborhood in subsequent analyses.
This has been extremely helpful to our purposes when choosing how to assess IRR for a coding study. I want to be sure I am interpreting some things correctly. We currently have 3 coders being trained in a coding system, and “standard” scores for the training materials that we are trying to match. We are trying to get up to a certain IRR before coding actual study data.
The way I understand it, we want to run two-way random ICC using mean ratings and assessing for consistency, using ratings from our coders and the standard ratings. This should should show reliability when our coders and the standard codes agree (or are consistent). When these ICC stats (we rate many dimensions) are above, say, .8, we should be ready to code real data.
We also may be interested in two-way random, single ratings, assessing for absolute match, between each one of our coders and the standard scores, as a measure of how well each individual is coding a certain dimension.
These three coders will be randomly coding real study data with some duplication for future IRR calculations. I think I am understanding the model we will use for those calculations will be different because we will not always have the same set of coders rating every subject, like we do with our training materials.
Am I on the right track?
If you want to assess how well you are hanging together with a particular value in mind – which it sounds like you are, since you have some sort of “standard” score that you are trying to get to – you will want agreement instead of consistency. Otherwise, if Coder #1 said 2, 3, 4 and Coder #2 said 4, 5, 6, you’d have 100% consistency but poor agreement.
You would also not want to include the standard ratings in computing ICC, since those would be considered population values – otherwise, you are including both populations and samples in your ICC, which doesn’t make any sense. You would be better off assessing ICC with only your sample, then conducting z-tests to compare your sample of raters with the population score (I’m assuming this is what you mean by “standard” – some sort of materials for which there is a accepted/known score – if this isn’t true, my recommendation won’t apply). Then compute a standardized effect size (probably Cohen’s d) to see, on average, how much your sample deviates from the standard scores. You would then need to set some subjective standard for “how close is close enough?”.
You would only need single measures if you wanted to see how well a single rater would code on their own. If you’re always going to have three raters, that isn’t necessary. However, if you are planning on using different numbers of raters in the future (you mention “with some duplication”), you’ll need to calculate ICC(1,1) to get an estimate of what your reliability will be in the future. You can then determine how reliable your ratings will be if you always have pairs versus always have trios doing ratings by using the Spearman-Brown prophesy formula on that ICC.
It sounds a little like what you’re trying to do is say “Now that we’ve established our raters are reliable on the test cases, we know they will be reliable on future samples.” That is unfortunately not really how reliability works, because reliability is both rater-specific and sample-specific. You have no guarantee that your reliability later will be close to your reliability now – for example, you can’t compute ICC(2,3) and then say “because our ratings are reliable with three raters, any future ratings will also be reliable.” That is not a valid conclusion. Instead, you can only compute ICC(1,1) to say “this is how reliable a single rater is most likely to be, as long as that rater is drawn from the same population as our test raters and our sample is drawn from the same population as our test population.”
So to summarize… if you plan to always have exactly 3 raters in the future for all of your coding, you should use ICC(2,3) as your best estimate of what ICC will be for your study data coding. If you plan to use any other number of raters, you should use ICC(1,1) and then use the Spearman-Brown prophesy formula to see what reliability is likely to be for your prophesied number of raters.
Okay. We do understand that the ICCs we’re calculating in training are not going to guarantee any level of reliability in future coding. The idea is in training to get to a point where we’re seeing the same things in our training material, and they agree with what has been seen in them before (the “standard” scores). The “standard” scores are of course still someone else’s subjective ratings and I don’t think we want to treat them as 100% accurate themselves. I think it’s ultimately, at least after the many hours of training we’re going through, more important that our coders are seeing the same things (reliable with each other) than that we agree all the time with the “standard” score.
But, we will not have these same three coders coding study material. We will have one (in many cases) and two (in some cases, to compute the actual IRR with study material), but not three. And, the study is going to go on long enough that in the future it will be coders trained in the future, not those we are training now, due to lab research assistant turnover, etc.
So it sounds like we should be assessing each coder’s reliability using ICC(1,1) between each coder and the standard score to estimate that coder’s future reliability? What if, as I say, agreement with other coders in training seems ultimately more important than absolute agreement with the standard score?
Thank you for your extensive reply. This is clearly somewhat above my level (I have not had grad stats yet!) but fortunately, I am not the final arbiter of these decisions. I will take this information upwards so we are sure to do this right!
If you’re going to be using different numbers of raters at any point in the future, and you want a prediction of that ICC in the future, your only option is ICC(1). Based on what you’re saying, I believe you’re interested in ICC(1,1) for agreement. I would not include the “standard” score, since this won’t be available to you in your actual study data and will affect your ICC unpredictably (it could artificially inflate or deflate the value). But you still might be interested in calculating Cohen’s d between your sample and that score, just to see how far off your coder sample is from that score, on average.
You also mention that in the future, you’ll be using 1 or 2 raters. If you do so, you will be unable to calculate ICC in the future, since ICC requires a consistent number of raters for all cases, and at least 2 raters. In that case, you could get an estimate of ICC by having two raters code a subset of the data and then calculating ICC(1,1) – by convention, you probably want at least 25% of your sample coded this way, but this isn’t a hard rule. However, that would not technically be ICC for your study – it would only be an estimate of that value (in a sense, an estimate of an estimate of reliability).
I’ll also mention that grad stats typically does not cover this area – although you can’t see e-mail addresses as a reader, most of the comments here are actually from faculty. Reliability theory is usually covered in a measurement, psychometrics, or scale development course (sometimes in research methods, but not always). Not everyone has access to such courses.
Thank you once more for being so helpful. I understand, I believe, that in training, I want to calculate ICC(1,1) for agreement with our three trainees’ ratings, since in the future we will be using single raters (not a mean) and we want to get the best estimate of reliability for any single rater since we will not be coding as a group. I don’t know if I’m phrasing all of this right, but I do think I understand (or am starting to).
And with real study data, we can never compute an actual IRR for all study data since most study data will be coded by only one coder. But 25% (as you say) is what we are planning to have coded by two coders, so we can estimate IRR (or as you say, estimate an estimate!).
And it seems we will still use ICC(1,1) with our two coders on that data, to get that estimate of an estimate.
If the applications I just finished submitting are viewed favorably, I will be a grad student next fall. Not faculty for a long time (if ever!) 🙂
Hi Dr. Landers,
Is there a way to get agreement statistics for each of the individual raters using SPSS?
Thanks!
Stefanie
I am not quite sure what you mean by “agreement statistics.” ICC assesses reliability – true score variance expressed as a proportion of observed variance. If you just want to see if a particular rater is not rating consistently with others, there are a couple of ways to do it. The easiest is probably to treat each rater as an item in a scale, and then calculate a coefficient alpha (Analyses > Scale > Reliability, I think), with the “scale if item deleted” option set. You can then see if alpha increases substantially when a particular item (rater) is removed. You can also do so manually with ICC by computing ICC with and without that rater. If you REALLY wanted to, you could also compute confidence intervals around ICC and compare with and without particular raters, but that is probably overkill.
Hi there,
This is an incredibly helpful article and thread. I want to make sure I am about to use an ICC appropriately.
1.) Can an ICC be used when item responses vary in number. For example, one question has 5 possible answers (5 point likert scale) while another question is a dichotmous Yes/no, and yet another question is a 3 answer yes/no/i don’t know.
2.) I have 4 different sections of a scale that are rated by parents and children. I am trying to determine an ICC for each section based on how well the family agrees with each other. Not every child of the parent will necessarily be participating. Which ICC is the appropriate one to use?
Best
Elissa
1) ICC is not appropriate unless you have interval or ratio level measurement. Your 5-point scale is probably fine (depending on the standards of your field). The Yes/No could be fine if you dummy code it, but I wouldn’t use ICC here. ICC is absolutely not appropriate for Yes/No/Don’t Know. You want some variant on kappa for this.
2) You cannot use ICC unless you have a consistent number of raters for ALL cases. So ICC is not appropriate in the context you are describing.
Dear Dr. Landers
i have a querry regarding which statistic to use for computing inter-rater reliability for my data. i have a collection of websites each of which being rated for a few dimensions by a number of raters. the number of raters is same for each website. the ratings are qualitative (i.e. good, average and poor denoted by 1, 2 and 3 respectively) for all the dimensions except one in which ranks are given. please guide me which statistic should i use for computing inter-rater reliability for my data. is it fleiss kappa that i should use? if yes, then how (using spss)? if not then which other should i use?
please reply as soon as possible
thanks
namita
If your ratings are all ordinal (good/average/poor and 1st/2nd/3rd are effectively the same measurement-wise), Fleiss’ kappa is a good choice. I don’t think you can do it in SPSS; but it is very easy to conduct in Excel.
Dr. Landers,
I am doing interrater reliability with a group of nurses (5) who staged 11 pressure ulcers. Based on your explanation, I should use 2 way mixed model with absolute agreement? Correct ? Thanks for your help, MDG
If they are all the same five nurses, yes. And assuming that the ratings you are talking about have a “real world” meaning, then yes – you are most likely interested in absolute agreement.
thank you dr landers.
i must clarify that in my questionnaire, there are certain aspects of websites on which each website (included in the list) is to be evaluated as good i.e.1/average i.e.2/poor i.e.3 and in the last, the users are asked to chose which websites according to them are top five (ranking them as 1,2,3,4,5). now should i calculate the reliability of these two types of items separately, i.e. the reliability of the evaluation part by using fleiss kappa and that of the ranking item separately by using kripendorff’s alpha?
please help me out
You should calculate reliability for each scale on which ratings are being made. Since you have a rating quality scale and also a ranking quality scale, you have two scales. Then, each scale should be assessed with an appropriate type of reliability.
so is it right to calculate reliability of rating scale using fleiss kappa and that of ranking scale using kripendorff’s alpha?
It sounds like both of your scales are ordinal, so you should probably be using the same approach for both. Kappa could theoretically be used for both. But for ordinal data, you would usually use a weighted kappa. I am not familiar with Kripendorff’s alpha, so I don’t know if that’d be appropriate.
dear sir
thank you very much for your suggestions.
Dear Dr. Landers
I have a question regarding which statistic to use for computing inter-rater reliability for my data. I have three raters who have rated images by their quality (0= non-diagnostic, 1= poor quality… etc. 5= excellent). The raters have looked 9 images stacks (with sightly different imaging parameters) and scored 10 image slices from each image stack. Can I use ICC (two-way random) to measure inter-rater reliability? or does it make any sence since the raters are in consensus in most of the cases?
Consensus doesn’t influence which statistic is appropriate – it should just be close to 1 if they are mostly in consensus. The only exception would be if they agree 100% of the time – then you would not be able to calculate ICC. I’d actually say that your scale is double-barreled – i.e. you are assessing both quality (1-5) and ability to be used as a diagnostic tool (0 vs 1-5). In that case, I’d probably use ICC for the quality scale and kappa for the diagnostic element (recoding 0 as “no” and 1-5 as “yes”). Given that you have high agreement, this would probably make a stronger case – i.e., you could say all raters agreed on diagnostic-appropriateness for 100% of cases, and ICC was .## for quality ratings. But that is somewhat of a guess, since I don’t know your field specifically.
Also, I’m assuming that your three raters each looked at the same 10 slices from the 9 stacks. If they looked at different slices, you cannot compute reliability (you must have replication of ratings across at least two raters to compute a reliability estimate).
Thank you. This was very helpful. So is it right to use 2 way random model with absolute agreement?
If your three raters are always the same three people, and they are all rating the same targets, yes – that is what I would use for the quality ratings component.
Hi Richard,
I wanted to run ICC(1) one-way random in SPSS. I have varying number of judges for each subject: each subject was rated by anywhere from 2 to 4 judges. All my subjects are in rows and the judges are in columns (judge1 – judge4). The problem is SPSS deletes missing data listwise and thus only subjects rated by 4 judges were included in the ICC calculation. Any suggestions?
Thanks in advance!
Jason
I’m afraid you won’t like my answer. Because ICC determines reliability given a particular number of raters [e.g. ICC(2,1) vs ICC(2,4)], one of its assumptions is that the number of raters is held constant. If you’re using the mean of this scale for a paper and can’t get 4 raters consistently, what I’d suggest doing is taking the first two raters for each case, calculating ICC(1,2) and then describing your calculated ICC as a conservative underestimate of the “true” reliability given your rater structure.
In reality, you’re going to have less reliable estimates of the mean when you have 2 raters than when you have 4. You could theoretically calculate ICC(1,2), ICC(1,3), and ICC(1,4) to determine reliability given each configuration, but I find that is generally not worthwhile.
I appreciate the quick reply. I poked around and figured out that using HLM I can estimate ICC(1, k) when k is not a constant. ICC(1) can be easily computed from the variance components in the HLM null model output.
On an unrelated issue, I ran into the ICC(2) versus ICC(1, k) issue you mentioned above: “some researchers refer to ICC(1,k) as ICC(2), especially in the aggregation/multilevel models literature”. When a reviewer does that, requesting for ICC(2) while probably meaning ICC(1, k), what would be a good way to respond?
The HLM ICC is not precisely an ICC, if I recall my HLM correctly. But it has been a while; hopefully it will be close enough for your purposes!
As for the reviewer, I find the best approach is to ask the editor (assuming you have a relatively friendly editor) who may be willing to relay your request for clarification to the reviewer. If you don’t want to take that route, I’d report the one you think s/he meant in the text of your revision and then explain in your author’s reply why you did it that way.
I selected ratings with only k = 3 judges and obtained the ICC(1) and ICC(1, 3) for the ratings in both SPSS and HLM 7.0. Both programs gave identical results. So that gave me some confidence in HLM’s computation of ICC.
Thanks for the advice!
Jason
Yes, that makes sense; as I recall, they should be identical as long as you have a consistent number of raters for each case and your sample size is relatively large. The differences occur when you have a variable number of raters; I believe it may change something about the sampling distribution of the ICC. If I’m remembering this right, the original (Fischer’s) formula for ICC was unbiased but required a consistent number of raters; modern formulas for ICC are based on ANOVA and do not require equal raters but are biased upward as a result. I suspect SPSS uses the first formula. But anyway, for your purposes, I doubt it really matters.
Hello Dr. Landers,
Thank you for this helpful post on ICC for interrater reliability. I am wondering if you have any insight on what would be an acceptable reliability coefficient (single-measures) for two raters that are rating the exact same cases. I have computed an ICC(2,1); the second rater has coded 20% of my data, as I am hoping to demonstrate the reliability of one rater who coded the entire set. I have not found many helpful resources for acceptable ICCs for interrater reliability in social science and educational research … some say above .70 for research purposes, while .80-.90 would be needed for major decisions (as with high-stakes testing, etc.). I got an ICC(2,1) = .76. I am happy enough with this, but I have been looking for a good citation to support the acceptability of this correlation and not having much luck.
Thanks for your time!
This is not going to be precisely an answer to your questions, but hopefully it will be helpful to you. All types of reliability are essentially the same in a particular measurement context. The difference between different estimators is what you treat as error variance. For example, a test re-test reliability coefficient treats differences over time as error, whereas coefficient alpha treats differences between items as error. In contrast, ICC(1) treats differences between rating targets as error, and ICC(2) treats differences between rating targets AND differences between raters as error. But all of these estimates try to get the same piece of information: what is the proportion of true variance out of observed variance? This is why the “best” measures of reliability tend to be the most conservative – because they consider multiple sources of error simultaneously (for example, the coefficient of equivalence and stability or generalizability theory overall).
The practical outcome of all of that is this: the lower your reliability, the more attenuated your effects will be (because you are mismeasuring your intended constructs) and the less likely you will find statistical significance even if the effect you want to find is present (i.e. increased chance of a Type II error). Low reliability also increases the standard error, making it less likely that any particular person’s scores actually represent their own true score (which is why very high reliability is recommended for high-stakes testing; even if group-level decisions are still predictive of performance, individual decisions will vary more than they should).
So the short answer to your question is this: since all reliability is the same, whatever standard you found for one type should be the same for other types, i.e. a .7 is a .7. But in practice, the lower that number, the less likely you find statistical significance (plus a variety of other negative consequences).
Thanks for the thorough response! That does answer my question. So am I correct in my interpretation that the ICC(2) is relatively conservative (it is the “better” measure) because it controls for both rater and ratee effects? I am actually preparing for my dissertation defense and I have a top-notch stats prof on my committee. Your blog and response have been extremely helpful!
In comparison to ICC(1), it is more liberal, because you must assume that your rater effects are the same across all of your ratings and then partial that out. But if that assumption is true, it should also be more accurate. ICC also still doesn’t account for temporal or other source of error. I’d strongly recommend reading Ree & Caretta 2006 in Organizational Research Methods and Cortina 1993 in Journal of Applied Psychology – they will fill many gaps in what I’m able to tell you on a blog post and comments!
Thank you! I will look at those articles. I appreciate all of your help!
Dear mr. Landers,
Thank you for your helpful post. You give really good exlanations. However, I still have some uncertainties about my own research, about which I have to write my masterthesis. I have conducted a study based on data stemming from a larger study on the same topic. Because I don’t gathered the data myself, and didn’t took off the measures, I have come to face some difficulties. One of the measures, of which I want to report the reliability in my Method’s section, consist of four stories from participants rated on a 7-point scale by two independent coders. From the ratings of those four stories, one composite score was created which yields the final score that is used in the analysis. Only I don’t know the separate scores of each coder for the different stories or the composite score. I only have one complete dataset. What I do have is the scores from one of the coders for 10 subjects and of that same 10 subjects I have the scores from the inventer of the measure, which did not rate the population of my study. Is it possible to assess interrater reliability between those to, even if I don’t know the scores for the other coder from my data? Wil it be possible to say something about the reliability of the test? I was thinking I could use a two way mixed ICC, absolute agreement but I don’t know if this is appropriate in this case. I hope you can help me. Thanks in advance!
Since reliability is population-specific, there is no way to calculate inter-rater reliability accurately in this context. The ICC you are talking about would be the reliability of mean ratings on that population for those 10 subjects, which is not the number you need. You must have all ratings to calculate reliability in this context. Otherwise, you are basically asking, “Can I calculate an ANOVA looking for interactions but not collect data for one of the conditions?”
Thank you very much for your quick response!! I was already afraid for that.. I will see what I can do now. Do you know if there is any other measure which I can use to say something about the reliability of the test? I hope that, in some way, I will be able to get to know the scores of each coder.
I’m afraid not. You can’t determine the reliability of scores you don’t have. What some people do in the context of meta-analysis is conduct a sort of “mini-code,” i.e. having the coders re-code a subset of the dataset and examine reliability on the subset only. But there are assumptions attached to that (e.g. that the recode they completed is parallel to the scores that were not recoded). But that is the only potential option I can think of.
Hello Dr. Landers,
We have calculated an ICC for inter–rater reliability and would like to make sure we are calculating and interpreting it correctly. We developed a 6-item evaluation tool to measure “Clinical Reasoning” ability in Medical Students & Residents. (They hear a case, and write a summary, and 3 raters have used this tool to rate their summary). There are 6 items on the tool, each rated with a 0, 1, or 2, for a total possible score of 12.
All 3 raters rated every participant, and we have a sample of raters, thus we computed a Two-Way Random Model. We are interested in Absolute Agreement.
We have four questions:
1. Single Measures refers to how accurate a single rater would be if he/she used this tool in the future, while Average Measures refers to the actual reliability of the 3 raters’ scores? Is this correct?
2. Cronbach’s Alpha is reported when we run the analysis. What does it mean in this context?
3. When we entered the data, we entered the total score (of the 6 item tool) for each participant across the three raters. So, we had 3 columns representing the 3 raters. Do we calculate the ICC on the data as it is or should we calculate the mean of total scores for each rater and run the ICC on the mean?
4. How do we know if EACH ITEM on the tool is reliable? Should we calculate an ICC for each item on the tool, in addition to the total score? (I hope this makes sense).
Thank you in advance for any guidance you may be able to provide.
I have 4 judges that are being used in combination as rater1 and rater2 to rate 30 responses. The four judges could be either rater 1 or rater2 for any response. Since I’m interested in the average rating is ICC(2,k) the correct procedure? Thank you.
Since you have inconsistent raters, you need ICC(1,k).
Thank you Dr. Landers for pointing out my oversight. Yes, I will be using ICC(1,k).
I was wondering, especially in my situation, what would have been the consequence of using a weighted Kappa? I had initially, planned to use that procedure.
Weighted kappa is going to be more appropriate for ordinal data – you can’t use ICC at all in that context. For interval+ data, I believe that weighted kappa approaches ICC(2,1) as sample size increases (at least, that seems to be the ICC referred to here: http://epm.sagepub.com/content/33/3/613.full.pdf+html). I believe weighted kappa will always be lower than ICC, but that’s a bit of a guess. I have honestly not looked into it too deeply, because I would just use kappa for ordinal and ICC for interval/ratio.
Hi, a lot of things to learn here: thank you! Could you, please, help me?
I have a group of 18 raters that rated twice 40 ultrasound images. It was a Likert scale : nothing, a little, a lot and full of.. Shoud I use ICC or k to test intra-rater / inter-rater agrement?
This really depends entirely upon the standards of your particular field. In psychology, for better or worse, we typically treat Likert-type psychological scales as interval-level measurement, in which case you would use ICC. But there are many fields where this is not standard practice. If it is not standard practice in your field, you should use kappa (or a variant). The easiest way to tell is if people typically report means of their Likert-type scales. If they report means, they are already assuming interval measurement. If they report medians only, they are probably assuming ordinal measurement.
I am struggling to write a null hypothesis for my doctoral dissertation. I am performing an ICC to determine reliability with 2 raters from a pool of 8 to rate 30 portfolios. Each portfolio will be rated 2 times. Any suggestions? My hypothesis is that there is no difference in the ratings… right?
If you are talking about the hypothesis test reported by SPSS, the null would be something like “this sample’s ICC is drawn from a population where ICC = 0”. I don’t know that I’ve ever seen a hypothesis test of an ICC reported, however, because you are usually just interested in the effect size (ie. what proportion of observed variance is estimated to be true variance?). The hypothesis test doesn’t really tell you anything useful in that context.
I am wondering about the assumptions that one needs to meet for calculating an ICC. Are they they same as for ANOVA? I spent quite a bit of reading on the internet about it but it is difficult to get a clear answer.
If I did interval-level measurement and would like to calculate an ICC to justify aggregating across different raters (I know which type to choose etc.), do we have to care about issues of normality and linearity? Are there any other assumptions that one needs to consider?
Is there an alternative to the ICC? Weighted kappa?
Your help will be much appreciated!
Yes, the assumptions are the same. ICC(2) is essentially a two-way ANOVA, with a random rater effect and random ratee effect. ICC(3) assumes a fixed rater effect. There is an assumption of normality of ratings and independence among raters and ratees. There is no assumption of independence of raters in ICC(1). Neither ANOVA nor ICC assume linearity. But if the normality assumption is not met, you should probably use a different measure of inter-rater reliability – kappa is one such alternative. Regardless, if your goal is aggregation, you can’t meaningfully aggregate using a mean if the normality and independence assumptions are not met – so such a change might fundamentally alter your analytic approach.
Thanks for your fast reply!
Just to clarify: The normality assumption refers to all the ratings per ratee, right? In other words, I need to check for normality of ratings for each individual ratee.
Technically, that is true. But in practice, you usually don’t have enough raters to reasonably make any conclusions about normality by ratee either way. ANOVA also assumes equality of variances between IV levels (in this case, between raters), so if that assumption is met, normality by rater is probably sufficient evidence – at least, that is what I would check. As with ANOVA, ICC is robust to minor violations of the normality assumption anyway – if everything looks vaguely bell-shaped-ish, you are probably safe.
Hello, Dr. Landers,
I have the same 2 raters rating a sample of 1000 people on the scale with 10 items with 5-point Likert scale treated as interval. I am interested in the measures of absolute agreement between the 2 raters. I plan to perform ICC(2,1) to calculate absolute agreement for each of 10 items.
But I am also interested in the total or mean agreement coefficient.
Is there a way I could calculate average ICC for a scale based on individual item ICCs? Or the only way is to use scale means for rater 1 and 2?
Thanks!
What you are saying is contradictory. If the 10 items are not part of the same scale, you would compute ICC for each of the 10 items. If the 10 items were part of the same scale, you would compute the scale mean for each rater and then compute ICC. There is no common situation I can imagine where you would do both, except perhaps in the context of scale development. “Mean reliability” is not usually a meaningful concept, because reliability as you would normally need to know it is sample-specific – the only situation where you’d identify mean reliability might be in the context of meta-analytic work (where you have access to a distribution of reliabilities).
Thank you for your comment. Yes, it is a part of reviewing a new scale and I wanted to provide as much insight about the scale as possible.
Dear Dr. Landers,
I would like to ask you a question about how to analyze inter-rater agreement.
I created a prosodic reading scale with 7 items. Each item has four possible options, each option is perfectly described.120 children were evaluated, 2 raters rate 60 children, and others 2 rater the other 60 children. To analyze inter-rater agreement, shoul I uses Cronbach? Kappa or ICC?
Thanks in advance, Nuria
Cronbach’s alpha is not appropriate, given your measurement structure. I am not sure what you mean by “four possible options.” If they are Likert-type measurement (implied by your use of the word “scale” and means the items could be considered interval level measurement, e.g. Very little, little, much, very much), and if you want to use the mean of this scale for something else, you should compute the mean score for each rater and then compute ICC(1,2) on the means. If all those “ifs” are true except you want to know “in the future, how well could a single individual rate a child on this scale?”, you should determine ICC(1,1). If you don’t have interval-level measurement, some form of kappa will be needed.
Dear Dr. Landers,
Thanks for your soon reply. It have been very helpfull.
I think I have a Likert-type measurement given that each options go from 1 to 4, and implies 1= a lower level in prosodic reading and 4 = the higher level. But the description in the scale is bigger. So, as you said, in this situation I should use ICC.
Another question is as I have 4 raters ( 2 evaluated the middle of the sample and the other two the other half. Could I do ICC( 2,1) with the first 2 raters, and the another ICC (2,1) with the other 2 raters, and finally report this two results?
Thanks again, Nuria
You should use ICC if your field generally treats such scales as interval – many do not.
You could report the results separately only if you treat the two halves as separate studies. If you plan to compute statistics on the combined sample, you must use ICC(1).
Dear Dr. Landers,
I have read your wonderful post and still have a couple of questions about ICC.
Three raters have rated 50 cases based on a validated 6 item scale using a 5 point Likert measurement. Three items of the scale measure one construct (e.g. expertise) and the other three measure another construct (e.g. trustworthiness). How would I determine the ICC between the raters? And how do I deal with the two constructs with respectively three items each? Should I compute the mean score for each rater per item or per construct? Or do you suggest something else?
Additionally, one rater only rated about half of the cases, while the other two rated all 50. How can I treat this problem.
Thanks in advance,
Monika
Compute the mean score per scale (one each for expertise and trustworthiness), then compute ICC on the mean scores. Unless you are using the individual items in later analyses, you do not need to know the interrater reliability of each item.
I would compute ICC(1,2), since you have a minimum of 2 raters for all 50. I would then compute means for use in later analyses across all three raters. Your calculated ICC will be an underestimate for cases where you have 3 raters, but you can still take advantage of the reduced error variance. You could also just drop the rater than only examined half of the cases and use ICC(2,2).
Dear Dr. Landers,
Thanks for your advice! Like you had suggested, I computed the mean scores per construct (trustworthiness and expertise) and computed ICC(1,2) on these scores. This resulted in an ICC value of .702 for the consistency measure and .541 for the absolute measure. I am now wondering:
– What do these ICC values tell me?
– What is an acceptable ICC value? .70 like Chronbach’s alpha?
– Are there other measures for interval variables I can use to check the inter-rater reliability between three raters?
Best,
Monika
This indicates that in terms of consistency (e.g. 1,2,3 is 100% consistent with both 2,3,4 and 4,5,6), your raters are assessing the same underlying construct (although it may not be the one you intend) 70% of the time. 30% of their ratings are error. In terms of absolute agreement (e.g. 1,2,3 is in agreement only with 1,2,3), your raters are assessing the same underlying numbers 54% of the time.
.70 is a moderately strong reliability, for both ICC and alpha. You really want in the .8s or .9s if possible. The side effect of low reliability is that relationships and differences you observe become attenuated; that is, if your reliability is too low, things that should have been statistically significant will not be, and observed effect sizes will be biased downward from their population values.
There are certainly many ways to examine inter-rater reliability; but for inter-rater reliability of interval/ratio data, ICC is the most common.
Dear Dr. Landers,
Firstly, what a privilege to read such a well written and student friendly article; clearly explaining the whole process. Additionally, I found it very refreshing that you have found the time to answer all the questions that have been posted. I do have a little question of my own if possible, but understand if you have had enough of us all!
I have a simple design whereby 5 raters assess all 20 muscle reaction times (ratio data). They repeat it again on a second day. I need to assess both intra and inter reliability.
For inter-rater reliability, I have taken the mean of the two days for each rater, and used ICC(2,1) as I am interested in absolute agreement and single measures. However, what statistic would you use for intra-rater reliability/ test-retest between the days? I know you mentioned Pearsons earlier in response to a post, but recent texts have recommended that because Pearsons is a relative form of reliability, a better approach is to use ICC for the relative form of reliability and SEM as an absolute measure of reliability. I wonder if you could share your views?
Thanks…. Pedro
The specifics of this differ a great deal by field – different areas have different “best practices” that are common, which I can’t really speak to. I’m not sure which “SEM” you are referring to (there are several), but this might be best practice in your field. In psychology, the answer is “it depends.”
If you believe that scores over the two days _should_ change (i.e. if differences between days can be due to variance in true score between days), then it is not appropriate to calculate reliability over time at all. If you believe that scores over the two days _should not_ change, then I am honestly not sure what you would do – it is not a common measurement situation in psychology to assess the same construct twice over time without expecting it to change.
Dear Dr. Landers,
Thank you for your unbelievably quick response; I have waited months for people in the statistics department of my University to get back to me. The SEM I was refering to was Standard Error of Measurement calculated as SEM = SD x SquareRoot (1 – ICC), but I shall consult my field on this.
Thanks for you honest reply regarding reliability over time. I would not expect them to change, but I shall investigate further.
One final question if I may… would it ever be appropriate to compute both an ICC to assess consistency and a seperate one to assess absolute agreement and report together?
Thank you once again!
Ahh… using SEM would be a very unusual standard. Although it does capture reliability, it is an unstandardized reliability (in the terms of the original measurement). Usually, when we report reliability (on theses, in journal articles, etc) we are doing so to give the readers a sense of how reliable our measures are, in a general sense (i.e. a reliability coefficient of .80 indicates 80% of the observed variance is “true” variance). When you report the SEM, that information is lost (i.e. the SEM is interpreted, “on average, how far do sample means fall from the population mean, given this sample size”). That is not usually terribly meaningful to a reader trying to evaluate the merits of your research.
Remember, reliability and measures of reliability are different. Each measure x measurement situation interaction has one and only one “reliability” – you are just trying to figure out the best number to capture that reliability given what you’ll be doing with those numbers later. It’s not the right approach to say “I’ll just calculate both” because then you are implying that both are meaningful in some way.
Instead, you should identify your goal in reporting reliability, and then choose a measure to capture that given your anticipated sources of error variance (e.g. time, inter-rater, inter-item, etc). If you are going to calculate statistics that only rely upon consistency on this data later (e.g. means, correlations, odds ratios), a consistency measure is appropriate. If you are going to use statistics that require precision, an absolute measure is appropriate. If you’re going to use both, then use both. But don’t calculate both just to report both.
Thank you for your advice; exceptionally clear, detailed and helpful.
Thank you.
Hi Dr. Landers,
Thank you so much for your article- my research supervisors and I have found this extremely helpful.
We do, however, have one question. You mention that there is one restriction for using ICC: there must be same number of ratings for every case rated. Unfortunately one of our data sets does not meet this requirement due to internet issues during online data collection. Is there some sort of accepted correction or cut-off, or must we simply collect more data?
Thank you,
Katelin
Well, keep in mind what you are saying. If you are using mean ratings, having different numbers of raters means that the amount of information you have about the true score for each case will be different. For example, one set of scores might be made up of 90% true scores and 10% error while another set might be 60% and 40%. That may not be desirable for your analytic purposes.
If that doesn’t matter to you, I believe there are techniques to come up with a mean reliability for your sample (in fact, it might even be as simple as a sample size-weighted mean of reliabilities calculated upon each set with different numbers of raters) but I have not used these techniques myself and am not sure what would be best in this particular regard. My approach is usually to randomly choose a subset of raters for each case so that all cases have an equal number of raters and then report the resulting ICC as a “lower” bound – assuming all raters are from the same population, adding raters should only increase reliability, after all. If your only purpose in calculating the reliability is for reporting (and not because you are worried that your scores contain too much error; i.e. your reliability is already high using this technique), this is probably sufficient.
Dear Dr. Landers,
Thank you for the clear information about ICC.
I still have a question about the ICC I would like to ask.
I had 33 parent couples fill in a questionnaire of 45 questions (5-likert sale) about their child.
I used Kappa for the inter-rater reliability of the individual questions and now I would like to use an ICC to measure inter-rater reliability of fathers and mothers on the 7 subscales.
Which ICC should I use? And should I use the single or average measures as shown in the SPSS Output?
Thanks in advance,
Florien
Since you have different raters for every case, you must use ICC(1). However, keep in mind that this assumes you believe the two parents to have identical true scores (i.e. you don’t expect their ratings to differ by anything but chance). Single vs. average depends upon your answers to the questions described in the article, i.e. it depends upon what you want to do with your subscale estimates. However, your question doesn’t really make sense to me, because if you used Kappa, that implies that you don’t have interval/ratio measurement and cannot compute ICC in the first place.
Dear Dr. Landers,
Thank you for your simple explanation. I would like to ask you about the significant level. I have conducted observations and have been rated by two coders. I’m using the two way mixed effect ICC and using the cutoff points of <0.4 is poor. From all 78 observations, there are several observations which have the average measure value higher than 0.40, but the significant level of more than 0.05. Do the sig. level play a role in selecting which observation to be included in my ancova analyses?
Thank you very much for your help on this matter.
Regards,
Iylia Dayana
I am mostly confused by your comment, because it is never appropriate to include or exclude cases as a result of reliability analyses. You should always include all cases unless you have a specific reason to suspect poor quality data (e.g. an error in coding). Otherwise, removing cases capitalizes on sampling error and artificially inflates your test statistics – removing them is unethical, in this case. If you calculated reliability correctly, you should also not have ICCs for each case – rather, you should have ICCs for each variable. Two ratings of one variable across 1000 cases will produce only one ICC. So I am not sure how to answer your question.
Dear Dr Landers,
This was extremely useful, thank you.
How would you calculate degrees of freedom for ICC? I have two fixed raters, and 30 observations.
Simon Morgan
P.s. I have used a two-way mixed effects model with absolute agreement – there are only two raters and the same sample of observations are being rated. If one rater is to go on to rate the entire population of observations, does this mean single measures is the most relevant statistic to use?
Thank you in advance
I am not sure what DF is for ICC, because I have never needed to test the significance of an ICC (this is a fairly unusual need – you’re asking “in a population where ICC = 0, would I expect to find an ICC this large or larger in a sample of this size?”).
As for your second question, yes – if you’re trying to generalize from two raters on a sample to one rater on another sample, you’d want the single measures version – but it is important to note that you will only have an estimate of reliability in your second sample, not an actual measure of reliability in that sample.
Dear Dr Landers,
I was wondering if you could confirm whether ICC is suitable for an experiment I’m analysing?
We have 6 pairs of raters; each person in the pair rates their own performance on 10 tasks and is rated by the other person in the pair (so 20 observations, 2 x 10 observations of self, 2 x 10 of other) .
We want to see how similar/different ratings are for own versus other. I’ve calculated the ICC for each of the pairings (ICC2), but is there a way to get an overall sense of rater agreement across all 12 raters for own/other? Can you average the ICC or is that too crude?
Also, in your opinion is two-way random the correct method (as opposed to ICC3 mixed?).
Many thanks
It sounds like you want the inter-rater reliability on each pair’s ratings. This is easy if you’re not interested in ratings on both members of the pair, i.e. if you have self and other from raters 1 and 2 respectively, but are only interested in ratings made on rater 1 OR rater 2. In such a case, you’d use ICC(1). In your case, however, you have non-independent data because you have two target ratings, i.e. if you included every rating target as a case, you’d have paired cases in your dataset. ICC does not have any way to handle this because it violates the independence assumption (you have introduced a confound of rater type and the individual rater).
In any case, you definitely don’t want ICC(2) or ICC(3) – you don’t have consistent raters for every case. These could only be used if you had the same two people rating all of your cases.
In your situation, I’d probably calculate two ICC(1)s – inter-rater reliability of ratings of self and inter-rater reliability of ratings of other. If they are not meaningful (if self and other are experimentally identical), then you could take a mean of these two ICC(1)s.
its good to know what you have explained
but i need to learn as i have seen in some papers as well
average inter scale correlation (AVISC)
sir what is this and how we can calculate it
using some softwate or what other means are possible
regards
I have never heard of AVISC, so I can’t help you there; also, this article is about ICC.
Thanks so much, will give it a try!
sir i am posting a refernce from one research a paper
paper
An empirical assessment of the EFQM Excellence Model:
Evaluation as a TQM framework relative to the MBNQA Model
journal of operations management 2008
Discriminant validity
Three approaches were used to assess discriminant
validity (Ghiselli et al., 1981; Bagozzi and Phillips, 1982).
First, for all scales Cronbach’s alpha was higher than the
average inter scale correlation (AVISC) (see 4th column in
Table 5). Second, the average correlation between the scale
and non-scale items (6th column in Table 5)was lower than
between the scale and scale items (5th column in Table 5).
That’s fine – you will still need to research it on your own. I am not familiar with it. It’s not a statistic I’ve heard of, so it might just be the mean intercorrelation between every possible pair of scales (likely squared, averaged, and taking a square root) but I do not know for sure. You will need to read the paper and figure it out.
Dear Dr. Landers,
thank you very much for the article, which has really helped me. However, a few questions remain.
During a scale development process, we have constructed 40 items with the following structure: First, a problem situation is described. Then, four (more or less effective) possible solutions to the problem are presented, which can be rated on a 5 point Likert scale.
As part of the development process, we conducted an expert survey, where 14 problem solving experts rated these four possible solutions (for each item) regarding their effectivity in order to solve the problem (on a 5 point Likert scale; they did exactly the same as the “normal” participants will do later).
In order to assess inter-rater agreement (with the goal of detecting “bad” items), I calculated ICC(2, 14) (consistency) for each Item (40 flipped datasets with 4 rows and 14 columns).
My questions:
Is this the right ICC I have chosen? For most Items, my ICC is very high (> .90). Is this “normal”? Descriptively, the agreement is quite good, but far from perfect.
In addition, I want to calculate an ICC for the whole scale (all 40 Items together; Items assess different facets of the same construct). If I remember right, you stated that in order to calculate the ICC of a scale, one should calculate the mean of the scale (for each participant) and then calculate ICC with these means. To me, this doesn´t make any sense, as I have only one row in my dataset then, which makes it impossible to calculate anything.
Sorry for the long post; I guess the structure of my scale is a bit more complex than usual.
Thanks very much for your reply!
Tom
This actually sounds like identical to something we have in I/O psychology called a situational judgment test. You might find helpful the more targeted discussions of reliability in the SJT literature. I am not super-familiar with SJTs, and there are probably specific techniques used for SJTs that will address the problem you are having. But in any case, you are right to suspect an ICC over .9 – any time you see a number that high, something is probably wrong somewhere.
I’m not sure your dataset is set up right. If you have 40 items with four situations each, you essentially have 160 items being rated. That would be 160 datasets, if you were interested in the reliability of each item on a target sample. Normally, you would take a mean of each dimension or scale and examine that instead (e.g. if you had four dimensions, you’d average across 40 items for each dimension within each rater and calculate ICC across four datasets). ICC may not be appropriate because you have no rating targets. We’d normally be interested in ICC when making ratings on some target sample – e.g. if 14 raters were examining 160 items on each of (for example) 50 experimental subjects (i.e. 14 x 160 x 50 = 112000 ratings).
In your case, you are missing the “subject” dimension – there is no target sample. The way you’ve set up your datasets, you are treating each problem situation as an experimental subject, i.e. you are assuming the problem situation is an independent rating target (which it may not be, since they are dependent upon their attached situation), and ICC assesses how consistently raters assess problem situations across the four solutions. So you may be violating the independence assumption of ICC, and you also may not have a valid sample (i.e. each of your four solutions must be considered a random sample from a population of solutions). I suspect there is a more standard way to examine reliability in SJTs, but I honestly don’t know what it is – but it is probably worthwhile for you to look into that literature for how reliability is assessed during SJT development.
Okay, thank you very much for the long and fast reply, many things do seem clearer right now. And especially thanks for the hint with situational judgement tests. I will look into it.
Dear Dr. Landers,
I’ve read all the questions on this excellent post, but I’m still not sure what to do about my own research. I’ve 25 essays, each rated by two raters on six criteria (resulting in a score between 1 and 10 for each criterium). In total there are five raters, each of them rated between 8 and 12 essays. I want to know how consistent the raters are in their rating.
I thought that an ICC, one way, would be most useful and that I should look at te average measure. So ICC (1,5) is the connotation in that case? My questions are:
1. Am I right about choosing ICC 1?
2. I’ve put the raters in the columns, the score for each criterium in the row. So some raters have 6 (criteria) x12 scores (essays) and others have 6×8 scores. Is it a problem that some raters rated more cases than others. Or should I have computed a mean for each criterium so that there a 7 rows instead of 48 for one rater and 72 for another?
3. In the next phase of my study the same 5 raters will rate another 25 essays, each essay rated by two of them. The same six criteria will be used but the depth of the description of the criteria is different from the first situation. If I do the same analysis I want to see if the second condition leads to a more consistent rating. Is that the right way to do it?
Many thanks if you could help me out with this.
1. ICC(1) is the right choice since you are using different raters for every case. You need to ensure that your five raters are split up fairly randomly though amongst rating targets.
2. That is not the right setup. You should have 12 columns (6 criteria x 2 ratings) and 12 rows (12 essays). You then compute ICC on each criterion pair, one at a time (6 analyses to produce six ICCs, the inter-rater reliability of each criterion).
3. In this case, you’d probably want to look at the confidence interval of ICCs produced the first time and ICCs produced the second time to see if they overlap (no overlap = statistically significant = different ICCs). I am not sure if the sampling distribution is the same in these two cases though, so that may not be a valid comparison. But that is the best I can think of, given what you’ve said here. If you are interested in determining changes in ratings from one set of criteria to the other, I’d probably have had half of your raters rate all 25 essays with the old descriptions and the other half of your raters do so a second time with the new descriptions, using a simple independent-samples t-test to analyze the results (or possibly MANOVA).
Dear Dr. Landers,
I am hoping you can provide some insight on my proposed design for rater allocation. Currently, I am proposing to use a one-way random model, as all subjects are not scored by all raters. I have 20 subjects to be scored, and have access to 8-9 raters. Therefore, I have 2 options:
(1) 8 raters. Pair raters so each pair scores 5 subjects. This results in a large overlap (e.g., rater pair 1,2 will score subjects 1-5; rater pair 3,4 will score subjects 6-10, etc).
(2) 9 raters. Raters not paired. As such, each subject assigned unique rater pair (e.g., rater pair 1,2 scores only 1 subject).
Since I am using a one-way random design, I would think the 2nd option would be most appropriate since each subject is assigned a random pair of raters. However, since the subject factor is the only source of variation, I am not sure it matters either way.
Any insight would be sincerely appreciated!
Many Thanks!
It doesn’t really matter as far as ICC is concerned which approach you take as long as its assumptions are met, especially in this case that your sample of raters is randomly drawn from a population of raters. However, I would choose the second approach for basically the reason you mention. Because there is a possibility that one of your raters is not as high quality as the others (i.e. that you don’t actually have a completely random sample of raters), I would consider a little safer to randomly distribute them among ratees – that way you wouldn’t have a consistent bias within the rater pair. But if you feel confident that your raters meet the assumption, it doesn’t really matter.
Thank you for your very helpful response. I have another follow-up question. As I previously stated, I am using a one-way random model with 20 subjects. I wish to calculate the reliability of 3 different components of a scoring rubric (ordinal scale):
(1) composite score, range 0-50.
(2) sub components #1, range 0-6.
(3) sub components #2, range 0-2.
I was planning on using a ICC(1,1) model, along with percent agreement to help determine if low ICC values are a result of low variability. For the sub component range of 0-2, I am not sure if an ICC model is appropriate. I know another option is weighted kappa, but given my one-way design, I am thinking this would not work. Fleiss (1973) showed the weighted kappa & ICC were equivalent; however, this was for the 2-way model.
Any insight is appreciated!
It has been a while since I read Fleiss (1973), but I believe that is a correct interpretation – kappa is equivalent to ICC(2) when data are ordinal and coded appropriately (integers: 1, 2, 3…k). However, I don’t see any reason you’d use different reliability estimates for a scale and its subscales.
Thank you for the very helpful page describing the differences between ICCs. I have an interesting study design and I am wondering if you could give some insight on how to get a 95% CI for the ICC?
In this design we have three separate groups of raters (~n=30, n=36, n=45) that were each asked to evaluate (yes/no) three different sets of 9 subjects each. Each set of 9 subjects was chosen to represent a range of disease severity, and the idea was that each set of 9 subjects would be fairly comparable. It is easy enough to calculate an ICC and 95% CI for each set of 9 subjects, but the challenging thing is to combine them to get an overall average ICC estimate and 95% CI for this average.
This would be simple to do if an SE for the ICC was provided and normal theory was used to construct the CI. However, all implementations that I can find for the ICC (in particular, I am using ICC(2,1)) provide a 95% CI but no estimate for the variance of the ICC.
Unfortunately, bootstrapping doesn’t seem reasonable here due to the fact that the 9 subjects were not randomly selected (not to mention the fact that there are only 9/survey). I also considered Fleiss’ kappa for multiple raters rather than ICC, but there is only an SD available for the null hypothesis (of no agreement) rather than an SD for the sample.
Do you have any ideas?
Thank you,
Anja
Since the 3 sets of 9 were not randomly selected, you are explicitly stating that you do not have a randomly drawn sample from a given population. A confidence interval will not be meaningful in such a context (nor will the mean, for that matter). But if you want to assume that your raters are all drawn from the sample population of raters and your subjects are drawn from the same population of subjects, I would probably just throw them all into one dataset and use ICC(1,1). If you have any such assumption violations, however, that won’t be a valid approach – and I don’t know of any alternate approach that would get around that.
Thank you for the very prompt reply! I did find an implementation of ICC that will run for the combined data in spite of the high degree of missingness –since each set of raters rates a different set of 9 subjects and there are no overlaps between the sets of raters. (I had tried this approach originally but the original ICC implementation that I found would not run.)
Yes, you are right I should use ICC(1,1) since the subjects are not randomly sampled.
It is interesting that the ICC(1,1) within each group was higher than the combined data (although the CIs overlapped):
group1: 0.45; 0.26 < ICC < 0.76
group2: 0.33; 0.17 < ICC < 0.66
group3: 0.40; 0.23 < ICC < 0.72
combined ICC(1,1) : 0.18; 0.12 < ICC < 0.30
I agree that the interpretation of a mean and a 95% CI are odd in this case (both within each set and across the three sets). It is agreement among randomly selected raters across a set of cases that represent the disease spectrum (and not the average case evaluated in practice). This design was chosen to help balance the sets and also to be able to observe evaluations at both ends of the disease spectrum. However, in terms of evaluating "overall agreement" this is certainly a study design limitation.
Thank you again for your help!
Actually, I did some probing around and I think the combined ICC is low due to the missing data which violates the ANOVA assumption that the ICC calculation relies on. Probably the best bet is to bootstrap the surgeons.
Dear Dr Landers,
I would be grateful if you could help me with an interpretation query?
I have calculated 2-way random ICC, absolute values on some rating scale data (13 raters, all scoring 16 ratees on 12 independent performance measures ). We are interested in the answers to 2 questions,
1) From a theoretical perspective (for developing the performance measurements), in this study how reliable were the raters at assessing each of the 12 performance measures?;
2) From a practical perspective, how reliable will these measurements be for assessing performance in the future, which will be done by a single rater?
To answer 1) am I right in thinking I need to look at the average measures coefficient and 2) the single measures coefficient?
If so, the coefficients are very different. The average rater coefficients are between .70 and .90 and therefore we had reasonable agreement. However, the single measure coefficients range from 0.18 to 0.51, which on the same scale are very poor. Does his mean our performance measures only likely to show reasonable reliability when used by multiple raters but not a single rater?
Many thanks
Yes, yes, and yes. At least as long there is no sampling problem with your raters (i.e. if one or more of your raters are substantially poorer quality than the others, or if there are non-randomly distributed individual differences among raters).
Great, thank you! We are investigating potential differences between raters next. They are a representative sample of our population of interest, but we suspect that some raters are better than others.
Dear Dr. Landers,
I am conducting a ICC (1,1) study. I am looking at both inter-rater and intra-rater reliablity using 20 subjects and 7 raters. However, this is in regards to a scoring system, so technically there is a “correct” answer. Therefore, even though I may find acceptable ICC values, it doesn’t mean they are valid. Consequently, I wish to compare an expert’s scores to that of my raters. This is to establish face validity, as it is subjective. I am not sure if I can simply use ICC (1,1)? I do not think a pearson correlation would be appropriate. I would be comparing 20 ratings computed from 7 raters to 20 ratings computed from 1 expert. It is also worth noting that the scoring scale is 0, 1, or 2 (ordinal). Technically, a pearson correlation would not be appropriate, only spearman’s.
Any insight is appreciated!
You are correct that ICC does not assess absolute agreement with a population value; only agreement among raters (i.e. do the ratings center around the same value?). There are a couple of approaches. Since you are using ICC, your data must be interval+ level measurement, so if you want to treat your expert’s score as perfect measurement (i.e. population values), I would suggest a simple z-test. No need to make it more complicated, especially if you’re just trying to provide evidence of face validity. Pearson’s/Spearman’s won’t work since you are assuming the expert’s judgment to contain population values (both Pearson’s and Spearman’s assume each variable is randomly drawn as a sample from a population).
Thank you for your helpful response! I have another question. I am also considering assessing the intra-rater reliability of both an expert (n=1) and trained raters (n=7). For the trained raters, I am using ICC(1,1) since no subject is scored by all raters. To use a ICC(2,1) design for trained raters isn’t plausible due to the time commitment required to score 20 subjects (needed for sufficient power). However, for the expert, it is possible to have him score all 20 subjects. Therefore, I can use ICC(2,1) for the expert.
I am wondering though if I should report ICC(1,1) for the expert, rather than ICC(2,1) to make results more comparable to trained raters? I am assuming the expert’s inter-rater reliability is superior to trained raters and I am not sure how to reflect this if I calculate each with a different ICC model.
Thank you for your help!
If you only have one expert rater, you can’t use ICC at all – ICC requires at least 2 raters (i.e. you must have a sample). So I am not sure what you mean by ICC(2,1) in this context. Any desire to calculate reliability for the expert also means that you are not assuming the expert rating to be error-free, which means you can’t use the z-test I recommended above. By definition, if you think unreliability will be a problem, you don’t have a population.
It might be helpful, in terms of research question framing, to think about which populations of raters you are interested in and which samples you actually have of those populations. One case does not a sample make. It sounds like you may have a n=1 sample from one expert population (useless for determining reliability since you need n>1 to have a sample) and one n=7 sample from a non-expert population. You either need to assume your expert is error-free or get a second expert.
I should have been more clear. Your z-test should work since I have an error free expert. This expert is allowed to use measurements to obtain correct scores.
However, for reliability, this same expert cannot use measurements to obtain “exact” scores. Therefore, his scores are not error free. My expert is from a sample from an expert population (n>1). I wish to calculate though the individual intra-rater reliability by having selected expert (n=1) score 20 subjects on 2 separate occasions. However, for the other non-expert raters (n=7), the same 20 subjects are scored, but using ICC (1,1). In this case, can I use ICC for the expert? And if so, which model?
Thank you again!
I don’t understand “I have an error free expert” followed by “his scores are not error free”.
You can’t use ICC if you have only one rater. Remember that all reliability estimates measure true score variance as a proportion of total observed variance. If you have zero observed variance between raters (sample of one), there is no variance to explain (reliability does not apply because you can’t divide by zero).
If you’re interested in test re-test reliability, you have 20 pairs of observations, so you can use a Pearson’s correlation between Time 1 and Time 2 data. But as an estimate of reliability, this does assume zero inter-rater variation.
At this point, you may need a statistical/methodological expert to be part of your project – it sounds like you have an unusual design, and someone on a local team may be best to work through these issues.
Dr Landers,
I wonder if you could clarify a few questions for me.
My study is examining inter-rater reliability of 3 raters who receive training on performing 5 tests compared to 2 raters who had no training.
Each rater performs all 5 tests on the same 20 subjects.
I would like to be able to generalise my findings to a wider population of raters ie will these tests be reliable in clinical practice.
Questions
1. Should I use a two -way random model.
2. Is it possible to have all raters combined to get a higher ICC value than each individual group of raters .
(e.g. Trained raters ICC value 0.93
untrained raters ICC value 0.83
all 5 raters ICC value 0.96)
If so why is this ?
Regards
Fran
1. Yes – I would use two 2-way random models, one for trained and one for untrained. Since you are trying to generalize to practice where a single person will be making that judgment, that would be ICC(2,1).
2. I assume you are asking why this can occur mathematically, and based upon your values, it looks like you are calculating ICC(2,k). The reason is because adding additional raters, as long as they are of similar skill at making ratings (same population), will always increase the ratio of true score variance to total variance (each additional rater will add error variance, but this variance will be uncorrelated with that of other raters; whereas the true score variance WILL be correlated). If you look at ICC(2,1), the values computed on all 5 raters should be somewhere between the ICC(2,1) of each of your other groups.
Dr. Landers,
I am hoping you could provide me with some guidance. I am the primary researcher and will be coding 70 videos using a 15-item scale. I will be the primary coder of all of the videos. I have two co-raters, each coding 35 of the videos. Which ICC should I use to run the reliability analyses considering that one of the raters remains constant while the other varies?
Thank you!
Diana
If raters are not 100% consistent, you must use ICC(1) because there is no stable rater effect to control for.
Thank you very much! My reliability was found to be fairly low (.5 range) and some variables had ICCs in the negative range. Qualitatively, the raters agreed on many of the cases and there was not a lot of variability in the ratings. Is there a way to account for the restriction of range and lack of variability when computing ICC? Thanks again!
I suppose you might be able to do a range restriction correction to get a population estimate of reliability, but that requires a lot of assumptions that are probably risky, and I’m not sure why you would do it in the first place. If ICC is negative, then some of your raters are responding in a reverse pattern from others – that is very severe disagreement relative the amount of variance available. A lack of variability will also play out in other statistics (attenuated correlations, for example), which exactly what a reliability estimate is supposed to tell you. That would suggest to me that you need to re-anchor your scale to increase variability (e.g. add more extreme response options).
Hi Dr. Landers. Discovering this site and reading the comments made my day. Thanks for being generous with your expertise.
Thank you so much! I’ve been scouring the internet trying to understand whether to use average or single measures and you are the only resource that explained this well enough for me to feel confident in my choice!!! Fabulous article!
Hi! Ditto on all those who commend your intellect and generosity! Here’s our scenario!
We would like to develop a new measure to support school admissions decisions. The measure has a rubric by which (once launched) any one rater (e.g., admission staff) would rate any # of new student applicants on 7 dimensions (e.g, academic, social, athletic…). Each dimension has only one rating/score, on a 5 pt likert scale 0-5. The total score would be the sum of the 7 ratings, possible range 0-35. in reality, any one student is rated by only one rater.
in measurement development efforts to date, 8 sample raters (e.g., staff) have used the rubric to each rate 15 different students (total: 120 students). no student has been rated yet by more than one test rater.
interest is in:
1. some indication that different raters can rate students similarly using the rubric once it’s launched.
2. some indication of the reliability of the measure, as used at this time only by the 7 “test” raters. and whether we could/would look at the total score (sum) as well as each of the 7 items.
the question is what’s the best next step w/ these test raters who have limited time to give. e.g.,
1. select a new sample of students (15-20 would be feasible) and ask ALL 8 raters to rate the same 15-20? or, alternatively with (i think) the same effect, ask 7 of the raters to rate the same 15 students the 8th rater has already rated.
2. create 4 pairs of raters among the 8, and ask each pair to rate its own new set of 15 new students so as to increase the total # of students rated (4 prs x 15 students = 60 students)?
or …! any other recommendation for some simple yet sound method for assessing this measure? Thanks VERY much for any suggestions!
If you can safely assume that each member of your staff is drawn from the same population of raters (i.e. if each is equally skilled at using this measure you’re developing), I would probably ask each of the raters to rate one student in your initial dataset that they haven’t rated yet (total of 240 ratings for 120 students), i.e. 15 more ratings for each rater. If those ratings are biased (e.g. if your staff are already aware of admissions decisions for those other students), then the second approach would be my second choice (60 students). However, I probably wouldn’t pair the raters – I would instead have a random pair rate each (i.e. still have each person rate 15 people, but randomly distribute the pairs). You definitely don’t want to take Approach 1 – the variability in 15 ratees just won’t be sufficient to get a stable estimate of reliability (your confidence interval would be quite large).
Thanks so much for your reply. Just to clarify your 1st suggestion: we’d ask each rater to rate 15 ratees (rather than “one”) that the rater has not rated before. If so, and if i’m thinking clearly (!), this suggests each ratee would end up with 2 ratings, 1 from 2 different raters. and, if so, is there preference if we 1) simply exchange full lists (of 15) among the raters vs. 2) take ~2 ratees from each of the 7 rater lists to distribute a different set of ~15 ratees to each of the “8th” raters? Thanks again!
Yes, that’s right. If you are absolutely comfortable assuming that all of your raters are equally skilled, you can just switch them in pairs since it is probably logistically easier. But I would usually recommend randomly distributing raters among ratees (so that each is rated by a different, random set of 2 raters). If you believe there to be some consistent trait across your lists of 15 that might be rated differently within group (e.g. if Group A is already more likely to be rated highly than Group B), then you might want to counterbalance groups across ratees such that raters always get a mix of groups. But that is really just insurance against unequal skill between raters or interactive effects between rater skill and target true score (i.e. if some raters are more skilled at rating people at the high end of the scale, and others are more skilled at the low end – not a very common situation anyway).
Sir, This is my problem.
There are ten sets of data obtained from ten mothers.
Seven specific questions( 7 variables) were selected from the questionnaire. Ten mothers were selected. Each mother was interviewed by all four data collectors where the same seven selected questions were asked by all 4 data collectors from each mother. The responses for the questions were given scores.
The columns are the scores given for each variable. The rows are the scores given by the four data collectors( there are 4 rows in each data set obtained from each mother).
If the response was’ Rarely’ the score=1, if the response was ‘Sometimes’ the score = 2, if the response was ‘usually’ the score=3, if the response was ‘always’ the score =4.
I want to see the level of agreement between the 4 data collectors in giving the scores for the 7 variables by checking the pearson r by using the data obtained from the 10 selected mothers.
You can’t use Pearson’s because you have four raters – Pearson’s only allows comparisons of 2. It also assumes consistency, but it sounds like you would want to know about agreement. As long as you’re comfortable considering the 1-4 scale to be interval level measurement (not a safe assumption in all fields), and if you’re using this data in other analyses, you’d want ICC(2,4). If you’re trying to generalize this measure to future uses by a single rater, you’d want ICC(2,1). If you can’t make the measurement assumption, you’d want Fleiss’ kappa (which is for categorical ratings across more than 2 raters).
For ICC, you will need to restructure your data. You’d want each rater/variable pair in columns (4 columns per variable) and independent cases in rows (10). Then you would calculate 7 ICCs, 4 variables/1 construct at a time.
Dear Dr. Landers,
thanks a lot for this helpful explanation! I was trying to follow your instructions, however SPSS stopped the operation telling me that I have not enough cases (N=0) for the analysis.
I did as you said: First, create a dataset with columns representing raters (e.g. if you had 8 raters, you’d have 8 columns) and rows representing cases. The difficulty in my case is that I do NOT have consistent raters across all ratees: I have 310 ideas being rated by 27 raters. Each rater rated only a subset of the 310 ideas, resulting in 3 ratings per idea (for some ideas only 2 ratings). Hence, most entries of my 310 x 27 dataset are empty. Is this the problem?
The ratings were based on 8 criteria with a 7-point likert scale each, and I have already used the mean values (e.g. 5.5) for each idea rating. I have run the ICC(1) analysis (one-way random).
I would appreciate any helpful comment. Thanks!
I just constructed a small dummy dataset, and figured out that SPSS was excluding all rows where NOT all raters did a rating. In your explanation you provide an example:
For example, if you had 2000 ratings to make, you might assign your 10 research assistants to make 400 ratings each – each research assistant makes ratings on 2 ratees (you always have 2 ratings per case), but you counterbalance them so that a random two raters make ratings on each subject.
This is similar to my case (except that I have 2 or 3 ratings per idea, this is not consistent). Now I am wondering how I should construct my dataset in SPSS
The problem is that you will have different reliability for each case – cases with 3 raters will be more reliable than those with 2 raters. You could come up with a way to assess “mean” ICC, but this is not a feature of SPSS. Easiest approach would be to only use two raters for each case, randomly selected from your three raters and report this as an underestimate of actual reliability in your dataset.
Thanks for your comment Dr. Landers! What I have done now is to use 260 ideas where 3 ratings are avilable and compute ICC(1,3) based on a 260 x 3 dataset. The selection of the 260 of 310 ideas can be deemed “random” because 1 rater simply did not make his ratings due to illness. The correlation coefficient (average) is 0.193 – which confirmed my supposition that the ideas have been rated quite inhomogeneously by the jury.
What’s been interesting is that the same ideas have been rated by idea contest participants, where I have 36 ratings per idea. Here I run ICC(1,36) analysis and the correlation is 0.771 – i.e. the ratings by the participants seem to be much more valuable (can I say this?). This was quite astonishing… although it partially could be explained by the larger number of raters per idea, I assume…
Although you might be able to consider it random, you still have fewer raters for some cases. That .193 is an overestimate of the reliability of your mean score. Also note that this assumes you are taking an average of judgments from each person – if there are any interpersonal processes that kick in later (e.g. If they discuss and come to group consensus), reliability will be even lower.
As for the other, that is not surprising – you have the equivalent of a 36-item scale. Almost any scale of that length would show at least reasonable reliability, even if it were multidimensional (which is likely is). In fact, the fact that it is only in the .7s means that your 36 are not really very consistent with one another. If you want to compare your two rarer samples directly, you need to compare the ICC(2,1), not the ICC(2,k). For more detail on scale length and reliability (applies equally well to ICC), see Cortina, 1993.
Hi Dr. Landers,
I have tried to make sense of your last comments on my results. In order to test the effect of “number of raters” on the ICC value, I have run a simulation where I compare 100-times ICC of random values (normally distributed ratings with significant sigma for 3 cases of 4 raters, 8 raters and 32 raters)… the result is stunning: While I only get around 30% (30/100) ICC values for the 4-rater-case above 0.7, for the 32-rater case (same random distribution of rating values) 100% of ICC values exceed 0.7
Now I understand why you said “Almost any scale of that length would show at least reasonable reliability”… But here’s the problem: What can I do to show (or argue) that the reliability of my 36 raters with ICC of 0.771 is actually quite bad?
If you’re interested, here’s my simulation: http://user-ideas.com/ICCtest.xlsm
Thanks again for helping 🙂
When in doubt, it is always good to check for yourself. 🙂 It is one of the things I talk about in my grad research methods course – if you ever see a scale with a moderate reliability but a very large number of items, it is either not a well-designed scale or the underlying construct is multidimensional.
In your case, I would take one of two approaches: 1) cite Cortina, 1993 who talks about this very issue (if I’m remembering this correctly, the table that I think would be particularly interesting is one where he simulates the joint effects of dimensionality vs. scale length on coefficient alpha) or 2) compare ICC(1,1)s. It is not meaningful to compare an ICC(1,3) with an ICC(1,36) anyway for the reason you just simulated.
Now I have a final question 🙂
I would appreciate a lot if you had an answer: I have seen that with my 310 ideas and 3 raters per idea (average) I get a pretty “bad” ICC(1,r) value. Now what I would be interested in is the question, if the raters at least were able to (reliably) classify the ideas into groups (e.g. top-5%, top-10%, top-15% etc.), and especially if they rather agree on the “best 25 ideas”. I am a bit confused if this question is actually an inter-rater-reliability question, but I guess yes.
The problem is that I do NOT have rater consistency, i.e. raters only rating a subset of ideas (thats why I use ICC(1,r)). Hence, I cannot really simply calculate the sum or average of my 3 raters per idea, because this sum/average depends on which raters I select as first, second and third.
My feeling is that I can only calculate the overall sum (or average) of 3 ratings per idea. Would I then use ICC(1,1) for checking rating reliability? Thanks again for your help!
It sounds like you want to polytomize ratings and check their reliability instead of the actual data. If you do that, you are artificially attenuating the variance in the original ratings (i.e. rather unscientifically hiding variance you don’t like). That is not a valid approach.
The lack of reliability means that your data collection did not occur reliably. That is an end-result, not a problem to solve with data analysis. The scales might have been poorly specified, the raters might not have been trained appropriately, or any of a large variety of other internal validity issues or combinations of issues. If you have poor reliability, you have poor reliability. The only solution is a new round of data collection with those problems fixed.
Hi Dr. Landers,
Thank you for your very helpful post! I am a bit confused about whether I should be using a one-way or two-way random ICC. I am working on a study in which therapists’ sessions are rated to determine if they are adhering to a specific therapeutic orientation. We conduct periodic consensus meetings in which many raters rate the same sessions to see if their ratings are reliable. The specific raters tend to vary from session to session (as does the number of raters rating each session) but they are all from the same pool of raters given that all the raters work in the same lab. Since the specific raters differ from ratee to rate, I am inclined to go with a One-Way Random ICC. Does this sound correct?
Thank you very much for your help with this!
Yes, that’s right.
Dear Dr. Landers,
I’d like to compute ICC for my study in which I have a rating scale that assess a construct comprising of several dimensions (multidimensional scale); each of the 10 subjects were rated by 2 raters but I have 3 raters working in combination. My questions:
1. Should I calculate/use the mean of the scale (all items) or mean of each dimension for each rater? I gather I shouldn’t calculate ICC on individual items unless I’m in a scale development stage, right?
2. The type of ICC would be ICC 1 (one-way random), and the general standard would be at least 0.7?
Thanks so much in advance.
I would calculate means by dimension by rater by ratee, then examine ICC for each dimension across raters. If an overall mean would be meaningful (ha!) for your multidimensional scale, I’d also calculate the overall mean for each rater by ratee. These estimates give you somewhat different information, so it depends on what you want to use those scores for later.
You should use ICC(1) since your rater identities vary by ratee. 0.7 is a reasonable standard as far as standards go, and that is all most journals will expect. Imperfect reliability only serves to make your observed scores less accurate representations of true scores (and also makes it more difficult to achieve statistical significance). Bigger is better – aim for .9 in your scale development process, if have the choice.
Thanks so much Dr. Landers. I really appreciate it. I wish u wrote a stats book for psychology, not just for business :))
Hi Dr Landers,
Thank you for creating and maintaining such a helpful resource!
I’m considering using ICC for IRR in my current research.
I have ratio data and will have either 2 or 3 coders in total.
I have currently coded all the data (about 200 participants), but intend for subsequent coders only to code data for 50 or fewer participants, given that it’s a lengthy process.
3 questions:
1. Is ICC appropriate in this instance?
2. Would I be using ICC(1) because the additional coders will not be coding all 200 participants?
3. Is there a recognised proportion of the data that subsequent coders have to code, such that the IRR derived speaks to the reliability of the scoring system in general?
Thanks in advance,
Daniel
1. Yes.
2. It could be either. If you’re going to add another coder to yourself, i.e. a total of 2, and you both have assessed 50, then you can calculate ICC(2) on those 50 cases. But to get a more accurate measure, I’d recommend trying to get every case coded by at least 2 people – so, for example, if you’ve coded 200, to ask each of your other two raters to code 100 (and then calculated ICC(1)). Remember that you can only calculate ICC when you have 2 or more ratings – if you only have 1 rating, that score will not be used in reliability calculations.
3. This is a somewhat dangerous practice. When you calculate an estimate of reliability for your sample, you are trying to capture the unreliability inherent to your particular measurement situation. If you only code a subset, you are calculating an estimate of an estimate of reliability. So I’d recommend avoiding that. I have seen published research that takes this approach (e.g. in meta-analysis) but its appropriateness is going to vary widely by context. I don’t think you could get away with less than 50%, but the closer to 100% you can get, the better.
Hi Dr. Landers,
I have done repeated measurements to determine the repeatability of a device. I want to see how repeatable the measurements are between days instead of between raters. Is it possible to use the intraclass correlation in this case? There are about 10 people that are being measured and the measurements between subjects are not expected to be similar, if that makes a difference.
I suppose you could – the better approach would be to use hierarchical linear modeling to explicitly model the over-time effects and report the effect sizes estimates (which includes ICC, I believe) from those analyses. Your sample size is quite small for this, either way.
Hi Dr. Landers,
Thank you so much for this article! It’s helped deepen my understanding of the ICC statistic, even after several attempts at reading the Shrout & Fleiss article, haha.
I have a question about the ICC that I still have yet to answer – can you use the ICC statistic when you only have ONE rater? For my dissertation, I used a new therapy (ACT) to treat a musician with performance anxiety. I was the only therapist in this study, and I had 2 raters independently rate my adherence to the ACT manual, using a scale called the DUACRS which measures ACT adherence. I’ve noticed that most examples of when to use the ICC involve multiple raters and multiple ratees. However, I’m wondering if I should use it in my study to reflect the inter-rater-reliability of the 2 raters for my adherence (I’m the only ratee)?
One solution I have is that the DUACRS has 3 sections to it (one for ACT adherence, one for CBT therapy, and one for Behavior therapy), and instead of having multiple ratees as a variable, I can have the multiple therapy styles be rated? For example, rather than entering multiple ratees into the rows of SPSS, I can enter “therapy type” ? Obviously the columns in SPSS will still be for raters (rater 1, rater 2).
So, visually this would look like this:
Rater 1 Rater 2
Therapy Type
ACT % adherent % adherent
CBT % adherent % adherent
Behavioral % adherent % adherent
What do you think? I greatly appreciate any feedback you can give me, as my dissertation would benefit from your expertise!
Cheers,
Dave
Dr. Landers,
I apologize the formatting of my previous email was bad. Basically, the Y axis variable in my study should be THERAPY TYPE (ACT, CBT, Behavioral) and the X axis variable should be RATER (Rater 1, Rater 2). And there will be 6 pieces of data, a percentage of adherence for each of the 6 conditions.
I hope that clears it up for you! Again, I greatly appreciate your help and have recommended this article to my dissertation chair!
Dave
It really depends on what you are trying to do with these estimates. I think the tendency is for people to think “I need to calculate some sort of reliability estimate for this paper” without remembering that we report reliability for a reason – it attenuates the very relationships and differences we are trying to investigate. By reporting it, we are telling the reader how much smaller the relationships we found are than they should have been if we’d had perfect measurement – and that is one of the reasons we can’t draw many substantive conclusions about a null result.
In your case, I am not sure why you are calculating this variable and why you want to know its reliability. If you want to know the reliability of a single rater for some reason, the only way to estimate that is to have 2 raters and then correct downward. Remember inter-rater implies “between raters.” If you only have one rater, there’s no way to know how that person’s scores match up to those of other people.
The data arrangement you are describing seems to imply that cases entered into analysis are no longer independently drawn from a population of interest – that is violation of the measurement model. So I wouldn’t suggest it.
Dr. Landers
Thanks for you reply! I apologize for not making my case clearer- I actually have 2 raters, and 1 ratee (myself). The question was can I still use the ICC with only one ratee ? All the examples I’ve seen of the ICC online seem to involve multiple ratees and multiple raters (as you pointed out in your reply). However, when there’s just 1 ratee and two raters I’m not sure how to conceptualize it or how to set up the rows and columns in SPSS for data entry.
The only way I thought to set up in SPSS was – having the columns be for raters (rater 1, rater 2) and the rows be for “therapy type” (therapy A, therapy B, therapy C). Normally the rows are for all ratees, but since there’s only one of me that would yield only two pieces of data (one rating from rater 1, one from rater 2). That’s not enough data for me. I want to know how good their level of agreement was for my performance on therapy A, B, & C. Is this still an ICC situation?
Ah, I see. Your idea of SPSS is not right – since there’s only one of you, you’d only have one row of data, not two – with one column for each rater/variable combination.
Agreement and reliability, like correlation, are conceptualized as “proportion of variance explained”. Since you only have one case, there is no variance to explain – so there is no way to determine reliability in the traditional sense.
You could set SPSS up with three cases, one for each type of therapy, but you change the referent dramatically – you are examining a population (in a statistical sense) of yourself – i.e. you are looking at how consistently people rate you as an individual. You would not expect that number to generalize to any other person. So I am not sure what value that number would really give you. If you’re interested in how consistently people are rating you, I would just look at mean differences on each variable across your two raters to see how much they agree in an absolute sense (e.g. “rater 1 was consistently 2 points higher” or “ratings seem random”). You don’t have enough data to do much else.
Thanks for the quick reply again! I am discussing this today with my dissertation chair, and we will take your advice into serious consideration! Your input helps deepen my understanding of the ICC, as I didn’t think it’d be possible to use with only one ratee, me.
I will have to do a simple correlation of their ratings to see if there’s any trend, as you suggest.
Thanks alot for the fast help,
Dave
Hi Dr. Landers,
I hope you’re doing well. Thank you for your previous guidance with the ICC situation for my dissertation last year, it was very helpful. You may remember, I conducted an N=1 study where I administered therapy on a participant and was then rated by 2 raters on how well I adhered to the therapy manual. You’d told me I couldn’t use the ICC to describe the IRR between the 2 raters in that scenario because there was only 1 ratee, me. My dissertation chair disagreed, but that’s another story…
I have now completed a follow-up study which repeated the same N=1 design. I used the same adherence rating system, where I had 2 raters rate my adherence to the therapy manual again. I’m wondering how I can describe the IRR between the 2 raters in this study ? If I can’t use the ICC value because there’s only 1 ratee and 2 raters, then what test, if any, can I use to describe the IRR between the 2 raters?
Each rater rated the same 3/10 therapy sessions, chosen at random. Their ratings are here, in case it helps:
Rater 1 Rater 2
How adherent I was in Session 4 0.1875 adherent 0.22159
How adherent I was in Session 5 0.17045 0.21591
How adherent I was in Session 7 0.10227 0.15909
You can see Rater 1’s ratings are consistently 0.04 -0.05 units lower than Rater 2’s. Is that the only way I can describe their ratings, or is there another test I can use to formally describe their ratings (i.e., simple correlation) ? The only ratings data I have is what you see here.
Thank you so much,
Dave Juncos
Hi Dr. Landers,
thanks for you great post on computing ICC.
I have one questions concerning missings. I actually want to aggregate individual-level responses to the org level and want to compute ICCs. I have 3-10 raters for every organization, in most cases three raters rated the organization. Each rater rates a 5-item construct. How do I compute the ICCs if I want to consider all cases and raters?
Thanks in advance!
Unfortunately, the procedure to do this is much more complicated than what is available in SPSS. You will need to use another analytic technique; I would use Hierarchical Linear Modeling (http://www.ssicentral.com/hlm/).
Dear Dr. Landers,
Thank you for the wonderful post. Could you please guide on the following:
In my study on Leadership, a questionnaire having 20 items was used and 5 items together make a leadership style scale making total 5 scales.
Leaders from different organizations were selected. Each leader was rated by his/her 2 subordinates on the 20 items. Could you please guide me how to compute Icc1 and Icc2 for these 5 scales in this case. Thank you.
It depends on what you want to do with the scale means. You probably mean ICC(1) and ICC(2) in the typical leadership/group research sense, which often refers to ICC(1,1) and ICC(1,2) in the Shrout/Fleiss sense. So I would calculate the 4 scale means and then calculate ICC for each of them.
Thank you so much Dr. Landers!
Could you please help me a bit more:
5 items make a scale or a leadership construct. Each item has 2 values by 2 subordinates.
Should I compute mean for each item for each leader averaging ratings by 2 subordinates?
OR Should I compute mean for the scale (all 5 items) for a leader using 2 ratings on all 5 items?
Two values, as in Yes/No? If yes, you need to code as 0 and 1. If no, you can’t use ICC.
Again, it depends on what you want to do with it later. If you’re only going to use the scale means in subsequent analyses, calculate the mean across the 5 items for each rater and calculate ICC(1,2) on the scale means across raters (you will end up with 4 ICCs for 4 scales).
Oh I am sorry here 2 values means 2 ratings by 2 subordinates. This is a Likert-type scale 1-5. Then ICC (1,2) will be ICC2. How to compute ICC1 or ICC(1,1)?
Thanks a lot!
Then yes, calculate scale means and use the instructions I wrote above for either ICC(1,1) or ICC(1,2).
Thank you so much for your great help!
Dear Dr. Landers, Thank you for your guidance! What are appropriate values of ICC1 and ICC2 which allows us to aggregate the data?
In my study Each leader was rated by his/her 2 subordinates and I have got some values for the 4 different leadership scales like this (N=150 leaders) from 9 different organizations:
F ratio p-value ICC(1) ICC(2)
2.03 0.000 0.33 0.51
1.76 0.000 0.26 0.42
1.68 0.001 0.25 0.41
2.10 0.000 0.34 0.51
There is not really a hard cut off. Assuming by ICC(2) you mean ICC(1,2), this indicates that only half (or less) of the variance shared between the subordinates could come from measurement of the same construct. The attenuation factor is .7 with that ICC – so any effect size related to whatever you’re trying to predict would be reduced by 30%, which also dramatically reduces statistical power.
I would not trust numbers that low – I would only be comfortable with ICC(1,2) above .80.
Hi Dr. Landers,
I am writing again to you (the last time I wrote was Aug 27, we’d discussed using the ICC for only one ratee, and 2 raters, and you’d told me that wouldn’t work) for help understanding an ICC scenario. I was told by my dissertation adviser that I could use the ICC to calculate inter-rater-reliability with only one ratee, since we’re not interested in generalizing the findings of our raters to the population. I went ahead and calculated the ICC’s but one was negative, and I don’t know how to interpret negative ICC value.
To refresh your memory, I administered a therapy for one client, and I had 2 raters independently rate my adherence to that therapy’s manual. The scale they used to rate me has subscales for 3 therapy styles (the therapy I used, plus 2 I didn’t use). As I understand, it’s the raters’ job to rate my adherence to the correct therapy, while also rating my in-adherence to the 2 incorrect therapies. The ICC I’m using would be ICC (3, 2).
After instructing SPSS to do a two-way mixed ICC, looking at consistency, My results were the following:
ICC (Therapy 1, aka the correct therapy) = 0.396
ICC (Therapy 2) = -1.167
ICC (Therapy 3) = 0.591
I don’t know how to interpret the negative ICC for Therapy #2. Do you? Is a negative ICC a reflection of poor inter-rater-reliability? Because the raters’ agreement for Therapy #2 was actually quite high, so I’m confused.
Thanks!
Dave
My understanding is that negative ICCs can be calculated in SPSS because a bias correction is used (although it is normally interpretable as a proportion like all reliability estimates, that proportion has been adjusted to account for small-N bias). Negative ICCs are not interpretable and usually result from peculiar sample characteristics (e.g. near-perfect agreement or near-zero agreement) or possibly violations of the underlying assumptions of ICC. The fact that it is negative would imply that you have an exceptionally small sample size, which would make the size of the bias correction quite large. But that is a bit of a guess – I’ve never looked that deeply into it. You’d need to dig into the SPSS technical manuals to be sure.
Thanks for the reply. If SPSS is constructed in that way, then maybe calculating the ICC’s by hand will give a different result? I can try that, using S & F’s formulas. Hopefully that will change the negative ICC’s to positive values.
Thank you for all of your help thus far. I am currently working on my dissertation examining the relationship between stress and parenting behaviors as rated during videotaped interaction. Two raters rated each variable and inter-rater reliability was assessed using ICC. Would you recommend using my single rating or the average of the two ratings for subsequent analyses?
Thank you!
Diana
If you’re trying to determine the relationship between your scale means and the means of other variables/outcomes, the average should contain twice as much information as either rating would alone.
Dear Dr. Landers,
Thank you for the foolproof ICC manual. I have a question relating to the rationale to use ICC in my study after reading your explanation of the mixed model. I had 11 raters (purposive sampling from an unknown population) to rate the importance of 91 indicators. These indicators were identified and selected to develop a set of indicators. Is it appropriate to use ICC (average measure) to evaluate the reliability of the instrument because the indicators were fixed, not random? That means the effect of the rate is fixed and the raters are sample but not random.
If it’s not justified to use ICC, then do you have any suggestions on which method I can use?
Thanks again and kind regards,
Q. Do
It depends on what you mean by purposive. If you’ve chosen raters that you believe to be representative of a broader population of raters (e.g. experts in the subject area), you can probably treat them as a random sample (though one drawn for their convenience). If your raters have different expertise, you might want to identify homogeneous subsets of raters within that group to examine in sets. I find it doubtful that you have identified 11 raters with completely distinct types of expertise to judge your scale, so you might want to think about what population(s) might be represented. Whether you end up with an overall ICC or subsets, the average is what you want, since you will be interpreting the average score provided by your raters to make judgments about the scale.
Thank you heaps, Dr. Landers.
As the 11 raters are from one area of expertise, and actually I think they are representative or I tried to achieve it at least. So your suggestion for the model in my study is ICC2, isn’t it?
I ran ICC2 and ICC3 in SPSS and the results are exactly the same: 2.01 for the single and 7.34 for the average (p=.000). And I’ll use the mean ICC 7.34.
However, one of my colleague who actually referred to your writing, says I can’t use ICC in this case because the indicators, as the ratees, are fixed, not random. What do you think about this?
Many thanks.
Q. Do
The random/fixed effects model distinction does not apply to the criterion, only to the predictors. You only need to worry about the assumptions of the general linear model (i.e. ANOVA, regression, etc) in the DV: it must be 1) normally distributed, 2) interval or ratio level measurement, 3) consist of independently drawn samples, and 4) homoscedastic with respect to raters and ratees. Since you technically have a population of outcomes (every possible indicator you are interested in), you don’t need to worry about the assumption of independence. You could also check the homoscedasticity assumption with a 2-way ANOVA and Levene’s test in SPSS, if you really wanted to, but the general linear model is pretty robust to violations of the homoscedasticity assumption anyway, so it is not something I’d worry about much.
Dr. Landers
Thank you for your dedication to keep the dialogue moving forward on this topic. Your help is very much appreciated!
I am conducting a quasi experiment (intact student teams). My unit of analysis is the student team (4 members each); however, I collected data at the individual (member) level. Each member completed a likert-type survey of 6 items to measure team viability (would they want to work together in the future as a unit). I averaged the 4 members score to create a new score (team viability score).
A member of my committee asked me to use ICC(1) to justify aggregating the individual member data into a team level variable by looking for statistically significant results.
My issue is when I calculated the ICC(1) of each team some of the ICC(1) were negative and not statistically significant. I spoke with another faculty member about the results. He said the reason could be the result of a small n (4). However, only 6 of the 24 teams had negative numbers. Thirteen of the 24 produced non statistically significant results.
I have been unable to find scholarly articles to help me understand how to interpret non statistically significant negative ICC(1) for aggregation justification. Would you say the issue with the negative ICC(1) is the same as you mentioned in the post to Dave Juncos (9/17/13)? I ask b/c I am not looking for reliability, but justification to aggregate.
Again, many thanks for your guidance.
I’d recommend taking a look at LeBreton & Senter (2008). I would not take a statistical significance approach because it is not what you want to know, i.e. if we were to assume there were no agreement in the population, how likely is it that this team would have agreed as much as they did or more? That is not a useful question. Instead, you want to know how much “real” information in contained within each person’s judgment and the overall judgment. That means effect size interpretation. LeBreton and Senter argue that you want ICC(1) – which is ICC(2,1) in the Shrout & Fleiss framework – to be above .05 and ICC(2) – which is ICC(2,k) – above .7.
For negative values, I’d take a look at Question 7 in that article. They deal with interpreting negative rwg, but the issues are similar. In brief, the likely culprits are low variance or violations of distribution assumptions (like normality). The aggregation literature suggests looking at multiple aggregation statistics for that reason – sometimes you will have high agreement but low reliability, and looking at ICC alone doesn’t communicate that well (see Question 18 too).
Thank you for the information and prompt response. I have the LeBreton & Senter (2008) article. I have reviewed it several times, and once more again today. I am now questioning if I am understanding the components of ICC calculations correctly.
From LeBreton & Senter (2008, p. 11) ” ICC is estimated when one is interested in understanding the IRR + IRA among multiple targets (e.g., organizations) rated by a different set of judges (e.g., different employees in each organization) on an interval measurement scale (e.g., Likert-type scale).”
Am I correct to run an ICC(1) on each team? Thereby comparing the ratings of each member of the team. The targets are the 6 items in the survey, and the judges are the individual members per team.
OR
Should I run the ICC(1) at the class (4 different classes) or total study (24 teams) level comparing all members of all teams ratings (on the 6 items) against one another?
Background on my study: I am conducting a quasi experiment (intact student teams). My unit of analysis is the student team (4 members each); however, I collected data at the individual (member) level. Each member completed a likert-type survey of 6 items to measure team viability (would they want to work together in the future as a unit). I averaged the 4 members score to create a new score (team viability score).
Very appreciative
I’m afraid you’re on the edge of my knowledge area here. When I do multilevel analyses, I always model multilevel effects explicitly – for example, by using hierarchical linear modeling. That enables you to ask group-related questions explicitly (e.g. do individual-level predictors or group-level predictors better explain the outcome?). I’ve never used ICC to collapse to a single level of analysis myself, so I am not sure about the answer to your question. But based on my understanding of ICC and the LeBreton article, my impression is that you would need to conduct ICC on each team, since you are asking how well individual perceptions represent the group average (the first approach you mention). You wouldn’t do this at the item level though – you’d want to compare the scale averages (i.e. how much of the observed mean score for each team member represent the aggregated team mean?), assuming your items are all on the same scale.
I would probably recommend a multi-level approach though. If you only have 24 teams and treated them quasi-experimentally aggregated to the team level, you have only n=24, which will be quite poor statistical power for between-team comparison (even worse if your quasi-experimental manipulation involves more than 2 conditions).
Much thankful.
Dear Dr. Landres,
despite using ICC many times in my studies i have hard time understanding in which case i will have to use single or average measures when my measured variable is an average of a N of trials. what do you suggest in this case?
Thank you,
Dina
I am not sure who is doing the ratings or on what in the case you are describing. However, if you are using averages of trials, you are probably interested in construct-level conclusions, which means you are probably using average measures for your analyses, which means you would use average measures for your ICC determination as well. However, I will note that if you averaging ratings across trials, you are missing inter-trial variance in your reliability determination, which may bias your estimate.
Dear Dr. Landres,
to make the case more clear, so the study is about evaluating the inter-reliability between 2 raters, and the measured variable taken (e.g. tendon thickness) was from average of 3 trials, each single trial was an average of 3 measures.
So based on your above comment i still should take average measures..?, However, in which way missing the inter -trial variance can bias my results?
Thank you,
Dina
Well, more technically, it just changes the referent. You’re determining the reliability of your raters when taking the average of 3 trials. You would not be able to generalize that number to what would happen with a single trial. If you want to know the “real” ICC, you might be able to use a 3-level hierarchical linear model (trials at level 1, target at level 2, rater at level 3), but I’m not sure – not a problem I’ve faced before.
If the study’s purpose is investigating inter-rater reliability in a particular context (or family of contexts), you will probably need something more comprehensive than a single ICC regardless.
Hello Dr. Landers:
I am trying to compute inter-rater reliability for Modified Ashworth Scale for rating spasticity on an ordinal scale with five (1, 1+, 2, 3, 4). I have two patients and twenty seven raters. What is the best statistic for this and is it available via GUI on SPSS.
Thank you
If your scale doesn’t have interval measurement, you can’t use ICC. You would probably need Fleiss’ kappa (3+ raters of ordinal/nominal data). I believe you can calculate Cohen’s kappa in SPSS (2 raters of ordinal/nominal data), but I think you’d need to calculate Fleiss’ kappa by hand/Excel or in R.
Thank you very much for such prompt response.
Shahzad
Dr. Landers,
This is an extremely helpful site. I am confused on one point I do not see addressed here. I have read that along with the ICC being >.70, you also need the F value for the ANOVA to be non significant. This non significant value indicates that there is no significant difference between raters, which is what you desire in reliability testing.
In my results, I have an acceptable ICC, but my F values for the ANOVA are significant. How should I interpert this?
Thanks,
Amanda
I believe your confusion comes from two implicit assumptions you are making evident in your questions.
Assumption 1) You are assuming that you either have “sufficient” reliability or not. This is a meaningless distinction. 0.7 is not a magical line that you cross and suddenly you have “enough” reliability. You always want “greater reliability.” The closer that number is to 1, the greater the extent to which the shared variance in ratings loads onto a shared factor (or factors). The further it is from 1, the smaller your correlations, standardized differences, etc. will be using that information.
Assumption 2) You are assuming that a finding of statistical significance means “the raters are different” in some meaningful way. The raters are obviously different, because they are different people. You have no reason to expect them to make 100% identical ratings, so finding statistical significance doesn’t tell you anything you didn’t already know. A finding of statistical significance in this context simply means that the differences between your raters are large enough to be detected by your sample size.
I would instead focus on interpreting the proportion you calculated, and deciding for yourself if you are comfortable with the degree to which imperfect reliability will make your measured relationships weaker when drawing conclusions.
Thank you!! I now understand better the significance and why I should not focus on that.
I have already done the work of combing through the literature and looking at future studies to help me define the ICC I will accept, so now I can move on in peace without fretting about the significance of the F value.
Hi there,
Thanks for your comments. It is really helpful. I have question:
I have 5 raters who rates 25 questions 1 or 0. I thought I should use the Fleiss’ Kappa for my case, as the data are binary and I have multi-raters. However, the Fleiss’ Kappa for my data becomes negative! I don’t know why? I tested many cases but this method seems doesn’t work for such data (this is a sample):
case1 1 1 1 0
case2 1 1 1 1
case3 1 1 1 1
case4 1 1 1 1
I think the Fleiss Kappa for this case would be more than 0.9, while it is negative. Am I using wrong method for finding the agreement among rates?
Could you please help?
Thanks!
That’s the right approach, but if that sample is really a good representation of your data, you may not have enough variance in ratings to get an accurate kappa (i.e. if most cases have 100% agreement). I would probably just report percentage of cases with 100% agreement.
Hello Dr. Landers,
Thank you very much for your post about the ICC! It is very helpful!
I hope you can help clarify one thing for me regarding the use of the “single measures” versus “average measure” ICC. I have 5 rating scales and 3 raters (population of raters) to rate 10 patients (3 times/visits per patient), thus resulting in 90 ratings by the 3 raters for each of the 5 scales. I am interested in the “absolute agreement” between our raters for these first 10 patients. I believe this would be a “Two-Way Mixed Model” with “Absolute Agreement”. Is this correct?
If we achieve “good” inter-rater reliability with the first 10 cases, our goal is to for the same 3 raters to split up and each rate a portion of the remaining cases (sample of raters). In order to justify dividing the effort among the same 3 raters for the remaining cases, should I use “single measure” ICC rather than “average measure” ICC? In future ratings, we’ll be using ratings made by all 3 raters but they will each be rating different patients.
Many thanks in advance,
Isabel
If you’re diagnosing patients, you probably have a sample of raters rather than a population of raters – unless you’re saying that the three people you have access to are the only people who will ever conduct such diagnoses, forever. If that’s not true, you want Two-Way Random with Absolute Agreement.
And yes – to justify dividing the effort between three raters, you’ll need to look at the Single Measure estimate.
Thank you Dr. Landers for your prompt reply. Yes, we’re indeed trying to diagnose patient of a neurodegenerative condition. For the purpose of this study, only these 3 raters will be rating all the patients. Thank you for clarifying the use of “single measure” estimate. Much appreciated!
This is such a useful site -thank you so much! I just want verification if I am doing this correct. I am doing observational coding on 200 interactions. I have one person rating all 200 (primary rater) and I have a second person rating 25% (or 50 cases). I want to determine the reliability of the primary and secondary raters on the 50 cases and generalize then to all 200 cases coded by the primary rater. So I know I have to use single measure since I only have 1 rater for the 200 cases. My question is do I use “one-way random” or “two-way random”. The one-way random is more conservative and so I’ve been advised to use it, but is it appropriate since I don’t have randomly selected raters?
If you don’t have at least theoretically randomly selected raters, it is not meaningful to have them do the ratings at all – otherwise, why would you ever conclude that this person’s ratings are meaningful, or could be replicated by anyone else? Assuming you really do have a sample of raters, you want two-way random since your raters are consistent for all 50 cases. However, you will be generalizing from your pair of raters down to your single rater for the other 75% of cases, so you must trust that other assumptions hold (e.g. that both the full sample and subsample are randomly drawn from the same population).
Just what I needed! Thanks a lot.
Dr. Landers,
Than you for this helpful website. Currently I’m working on my thesis, to understand the writing ability of English language learners I should apply inter rater scale of measurement .I have two rater who must correct the writing papers of students according to four scale of CONTENT, ORGANIZATION, VOCABULARY, LANGUAGE, MECHANICS, and the ultimate score will be the mean of scores in these 4 scales. I would be thankful, if you help me to select a reliable inter rater measurement in the context of language learning and how i can calculate it by my hand on around 5 or 10 sample papers which is corrected by two raters?
You’re mixing some concepts, which is making it difficult to figure out what your’e asking. Interrater is not a scale of measurement; it is a way of looking at reliability (consistency) of measurement between raters. ICC as a measure of inter-rater reliabiltiy assumes either interval or ratio scale of measurement. So you need to figure that out first. If you do have interval+ scale of measurement, ICC would be fine. IF you always have the same 2 raters, you should probably use ICC(2). If you have different pairs of raters of raters for each, you should use ICC(1). If you are interested in your four subscales separately in further analyses, I’d calculate 5 ICCs – one for each subscale and one for the overall scale mean. If you’re only interested in an overall assessment, you only really need the overall mean (one ICC). If by hand you mean without SPSS, this is fairly straightforward if you understand ANOVA – you need a dataset with every rating on its own row, rater identifiers in a second column, and ratee identifiers in a third row. You then conduct an ANOVA (for ICC(1), ratee as IV and scores as DV; for ICC(2), ratee and rater as IV and scores as DV) and run through the ICC formulas from the ANOVA table – for ICC(1,1), (MSb-MSw)/(MSb+MSw(k-1)). Or (MSb-MSw)/MSb for ICC(1,k). It is slightly more complicated for ICC(2,1).
Dear Dr. Landers,
Thank you so much for replying me , according I understood that those 4 scales ll make me more confused and I decided to measure the raters correlation according the total numbers they give to students. Before the raters start to rate the papers of my final subjects for study , how many subject’s score is enough for understanding the agreement of raters according to ICC??? for example here i provide a table and the numbers are all examples and the scores are out of 100 , I would be so thankful if you show me the formula and how to calculate manually the ICC for these sample data ?
student rater A score rater B score
1 50 65
2 85 95
3 80 85
4 90 87
5 71 92
sorry if the figures didnt reach to you by order. first row is number of students , second row is scores give by teacher A, third row is scores give by teacher B. Also these two teachers ll rate one time means there is no pretest or post test just one pepper of composition. thank you , Im waiting for your kindly reply.
I’m not sure how much I can help you beyond what I’ve told you already. If you want the formulas for ICC, they are in Shrout and Fleiss (cited above). You’ll need to first calculate the ANOVA appropriate to the type of ICC you want, then use the formulas derived there.
In terms of precision of ICC, the number of raters is nearly as important as the number of cases. You probably won’t be able to get a stable estimate of ICC(2,1) with only 2 raters. You can algebraically manipulate the ICC formula in Shrout and Fleiss to solve for k – that will tell you the number of raters you want for a given level of ICC(#,k).
Dr. Landers, i hope you can help me.
I am currently conducting a reproducibility study on 26 young swimmers. I have measured their jumping height on two occasions, all measurements were performed by myself.
Which ICC is appropriate for my design?
So far i have only calculated ICC by hand using ICC (1,2) according to Rankin and Stokes (Reliability of assessment tools in rehabilitation: an illustration of appropriate statistical analyses), but i can’t figure out which one of the ICC’s is appropriate for my study design according to Shrout and Fleiss.
I am to calculate ICC i SPSS, so i hope you can help me.
Best regards
Melene Lykke.
You are violating the assumptions of ICC by rating it twice. ICC(1) assumes a randomly drawn rater for every rating and ICC(2) assumes the same pairs (or trios, etc) of raters for all cases. In your case, you have neither. However, if you consider each of your measurements to be essentially random, you could use ICC(1), as your book suggests. The mapping of ICC(1,k) to SPSS commands is explained in the article above – one-way random, average measures.
Thank you for your reply. I wasn’t aware of the assumptions of ICC. I will follow your recommendation of using ICC (1).
Again thank you.
Dr. Landers,
Thank you so much for such a clear explanation. I have an unusual question involving a robot performing a rating as opposed to a human.
If I use a testing system to measure say joint motion but it does so automatically/robotically. I am interested in finding the reliability of that testing system over days. So if I construct a study to measure 10 subjects over 6 days with 3 tests per day, would the ICC score be a means to calculate its reliability?
Each test requires that the subject be placed in the testing system the same way which is performed in a routine fashion. The system then automatically calculates the subjects joint motion. The system itself has been studied to show that it reliably performs the measurement tasks and reproducibly calculates joint motion in an artificial test to within 0.5 mm and 0.1 degree.
I would now like to calculate the reliability of the testing process on subjects. I would think that each test would act as an independent rater over days/number of tests. Furthermore, I would think that the testing system would be the ‘ideal’ rater. Thus, the ICC(3,k) would be utilized.
Do you agree or can you shed some light on this situation?
Thank you so much,
Tom
Well, keep in mind first that a system itself cannot be reliable or unreliable – it only demonstrates reliability in a particular measurement context given particular rating targets. I am not sure what you are trying to measure exactly – if you’re interested in the reliability of the system in detecting joint motion from a particular population of joints over time, I don’t see why you would want so many measurements. Remember that any time you chose a reliability coefficient, you must think about the sources of error that you want to assess. It seems like you’re most concerned about temporal error – changes over time – in which case, why worry about both multiple tests per day and tests over multiple days? Do you expect different error rates depending upon the time span? I would choose just one (e.g. one rating per day over x days or x raters in one day) unless you expect such a difference. If you DO expect such a difference, you have a fairly complex relationship between reliability and time and may need to create your own reliability estimate if you wanted to capture that. If you don’t want to do that, I would instead model those differences explicitly (e.g. variance over both the short and long term). 18 measurements of the same number is quite a lot though.
In this context, you do not meet the assumptions of ICC 1, 2 or 3. However, if you don’t mind relaxing the random-rater-draw assumption, you could feasibly use ICC(1,k). If you’re interested in the reliability of a single joint measurement (which it sounds like you probably are), you’ll want ICC(1,1). This would be interpreted as a test re-test reliability (sort of) rather than an inter-rater reliability though.
As a side note, you will also need way more than 10 subjects to get any precision at all in any reliability estimate. Otherwise your standard errors will be huge.
Dear Dr Landers,
Thank you for generously taking time to educate those of us who are less familiar with ICC. I’ve been searching the Internet for days looking for information on this topic and have not been able to find useful webpages- yours is the closest to what I was looking for. I don’t believe my questions have been addressed previously in this thread, and hope that you might be able to help!
I have a balanced panel dataset with a sample of 900 firms in 194 industries spanning 9 years. I have three levels – time, firm, and industry. I need to decide the appropriate level of aggregation for each variable. That is, I must decide whether each variable should be regarded as transient (varying over time) or stable (ie explains only cross-sectional variance between firm or industry). The literature indicates that ICC(1) can be used to answer this question, and ICC(2) can estimate the reliability of the aggregate measure.
My questions:-
(1) According to Bliese (2000, p 355-356), the formula to compute ICC(1) based on one-way random-effects ANOVA is as follows:
“ICC(1) = [Mean Square (Between) minus Mean Square (Within)] / [Mean Square (Between) + (k-1)*Mean Square (Within)].”
Bliese (2000) defined k as the group size. In my study context (where there are 3 levels – year, firm, industry), what number should I plug into k for each of the 3 levels?
(2) Given that my study context has three levels, should I run one-way random-effects ANOVA three times whereby each grouping factor is time, firm, and industry in order to determine the ICC(1) for each level?
I would be grateful for any guidance you can provide!
In the aggregation literature, ICC(1) usually refers to ICC(1,1) and ICC(2) usually refers to ICC(1,k). That is the Bliese interpretation as well – you can see that his formula for ICC(2) is really ICC(1) with a Spearman-Brown correction (which is consistent with ICC[1,k] in Shrout/Fleiss).
When answering aggregation questions, you’re not really interested in the higher levels organizing your data given a particular question. You just want to know if the most basic unit within your data (the one you are aggregating) is meaningful. So you could run a one-way random-effects ANOVA at the bottom level of your model (either firm or time, I imagine). If you wanted to aggregate across multiple categorizations, you’d need to create a new grouping variable indicating that group membership (e.g. for each unique combination of industry/firm).
However, I would recommend not doing any of that because you still lose information that might be important in later analyses, and it will be difficult to justify the particular aggregation strategy you end up using in a research paper given that you have a variable hierarchy (time within firm/industry or firm/industry within time). Hierarchical linear modeling (or linear growth modeling in the context of SEM) do not require such sacrifices. So I would use one of those approaches (and that will be an expectation of reviewers in many top journals, e.g. AMJ, anyway).
Dear Dr Landers,
Thank you most kindly for your prompt response!
Here’s a sample of my data structure:-
Firm_name TimeFirm_id industry_id
ABC 1234 3576
ABC 1234 3576
ABC 1234 3576
ABC 88553510 3576 4.00
So you’re saying that I should just run a one-way random-effects ANOVA using time as the
Dear Dr Landers,
Thank you most kindly for your prompt response! I apologize that my prior reply accidently got sent before I was ready.
I have a couple of clarification questions.
Here’s a sample of my panel data structure:-
Firm_name Time Firm_id industry_id Firm size
ABC 1 3576 0011 1.11
ABC 2 3576 0011 2.10
ABC 3 3576 0011 1.89
.
DEF 1 1234 7788 1.11
DEF 2 1234 7788 2.10
DEF 3 1234 7788 1.89
Let’s say I want to determine whether firm size is a transient or stable factor.
My questions:
(1) If I understand correctly, you’re saying that I should just run a one-way random-effects ANOVA using time (the lowest level) as the grouping factor and firm size as the dependent variable?
(2) In order to compute ICC(1) using Bliese’s (2000) formula, what number should I plug into k, the group size? Since I have 9 years of data, is k=9 in my case? I’m a little confused because I’ve also got 900 firms in 194 industries, so would my group size “k” be the number of years of data (9) or average number of firms in each industry (900/194=4.64)? Bliese (2000) gave the example of average number of teachers per group as 40.67 for “k”, but I suppose that was for multilevel modeling. Since I’m using growth modeling involving time, perhaps my k should be 9?
Thanks for your patience with my questions! I’ve been reading the literature quite a bit but I’m still relatively new at this, so please pardon me if these are basic questions.
If you’re interested in calculating ICC, the score you are interested in is your DV, whereas your grouping variable is your IV, whatever that grouping variable might be. I am confused by your other question, because if you are using growth modeling, you should not need to aggregate in the first place.
Dear Dr Landers,
I apologize for not being clear. Let me try to explain again. So I have three levels – time, firm, and industry. I’m interested in using ICC(1) to examine the amount of variance in firm size that occurs within firms over time versus between-firms versus between-industry levels. Based on Bliese (2000), I know that I need to use one-way ANOVA with firm size as the dependent variable and time as the grouping factor (or independent variable).
Let’s say the one-way ANOVA result for firm size is as follows:-
Sum of Squares df Mean Square F Sig.
Between Groups 58.400 11 5.309 2.040 .021
Within Groups 23830.728 9155 2.603
Total 23889.128 9166
Now, I need to compute ICC(1). Based on Bliese (2000), the formula is as follows:-
“ICC(1) = [Mean Square (Between) minus Mean Square (Within)] / [Mean Square (Between) + (k-1)*Mean Square (Within)].”
Using the one-way random effects ANOVA results above, I plug in the following numbers:-
ICC(1) = [5.309 – 2.603)] / [5.309 + (????-1)* 2.603]
I’m not sure what value to plug into k here as depicted by ????. That’s the essence of my second question. But perhaps I’m misunderstanding how the whole ICC(1) thing works in growth modeling. If that’s the case, I would appreciate your advice to help me understand how to determine ICC(1) in growth models.
Thank you so much again!
Ah. In your example, you would use the number of time points for k.
My instinct is still that you should not be aggregating, but blog comments are not a very good forum to figure that out for sure. 🙂 I’m sure you’ll be able to explain it in your paper, so no need to worry about it.
Thank you so very kindly, Dr Landers! I greatly admire your generosity in sharing your knowledge and time with someone you don’t know. Happy Holidays to you!
Dear Dr. Landers
Thank you so much for your article, it is really helpfull!
I´m doing some research where I use ICC to test for agreement between two raters.
I choose two-way mixed –> absolute agreement –> single measures.
My question is: I know that 0,70 is a cutt-off score that people typically use when they interpret ICC, but since i test absolute agreement, should i still use this value? Or should i use other values that is often used for interpreting agreement – for example suggested by Fleiss (1981): “0,0 – 0,4” ; “0,40 – 0,75” ; “0,75 – 1”?
It depends entirely upon what number you find to be realistic and worthwhile. The further from 1.00 your reliability estimate is, 1) the more difficult it will be for you to find statistical significance and 2) the more likely your scale will be multidimensional and measuring something you don’t realize it’s measuring. I would personally not trust a scale in my own research that does not typically demonstrate reliability over 0.85 in the type of sample I’m using. Whatever your cutoff, agreement vs. consistency should not affect the cutoff that you find compelling – the agreement vs. consistency question is driven by the research question you’re trying to address.
Dear Dr.Landers
Thank you so much for the article.
After having read so many comments and replies I’m still not able to find the exact way to work on my paper. My work is on pain reactions in preterm babies. I have 4 raters who have rated the same 20 babies across 20 variables with a yes or no (whether they see the particular pain reaction or not).
It looks like I cant use ICC because the ratings are yes/no and I cant use kappa because I have more than 2 raters. I read some where in these cases that I can use the Kendall’s coefficient of concordance. Do you have any suggestions for my scenario? Your answer would be greatly appreciated.
Thank you!
Kruthika
By “kappa”, you probably mean Cohen’s kappa. Fleiss’ kappa is a more general case of Cohen’s and can be used with any number of raters. However, you could also use ICC by coding your yes/no ratings as 1/0. If your 20 variables are all part of the same scale, I would probably take a mean yes/no (1/0) rating, i.e. each person’s score is the percentage of yeses they answered, and calculate ICC on that. I would not use ICC to determine the reliability of individual yes/no ratings, because dichotomization will depress your estimates in comparison to kappa. Kendall’s W is used when you have rank-order data, which would also technically work here, but is less common.
Dear Dr. Landers,
Thank you for such a clear and quick reply!
Dear Dr Landers,
In our study we have determined the intra and interobserver reliability using ICC ( 4 raters, 51 cases, 8 options). Now we would like to have a 95 % CI of the mean ICC of the 4 observers ( inter and intra). Do you know how to determine the 95 % CI of the mean ICC?
Thanks for your help
It doesn’t sound like you’d need a mean ICC in the situation you described. And I don’t know what you mean by “intra-observer reliability” unless you had multiple scale items, in which case you probably wouldn’t use ICC. You should be able to calculate one inter-observer reliability estimate in SPSS given that data, and it will tell you the 95% CI by default.
Hi Dr. Landers,
I’ve read somewhere that the ICC can also be used to determine if there are predominantly trait or state differences between people. For example, if after a series of repeated measurements of the same function (lets say “alertness”, measured 10 times a day), the intra-indiviual variance (within-subjects) is less pronounced than the inter-individual variance (between-subjects); then a trait-like operation is underlying the function. Put differently, the higher the intra-class correlation, the more likely it is to expect effects to be stable over time.
Now, I have such measurements, but I fail to be sure which model I should use to compute the ICC, and which result to report (single or average). Could you formulate some advice? Thank you in advance, and congrats on the article.
I would like to help, but I have unfortunately never heard of this. I think you’d be best off finding an example of this in prior literature and replicating their approach.
Thank you Dr. Landers.
I found the article I was talking about: J Sleep Res. 2007 Jun;16(2):170-80.
Trait interindividual differences in the sleep physiology of healthy young adults.
Tucker AM1, Dinges DF, Van Dongen HP.
That’s what they say about it: […] Among 18 sleep variables analyzed, all except slow-wave sleep (SWS) latency were found to exhibit significantly stable and robust–i.e. trait-like–interindividual differences. This was quantified by means of intraclass correlation coefficients (ICCs), which ranged from 36% to 89% across physiologic variables, and were highest for SWS (73%) and delta power in the non-REM sleep EEG (78-89%). […]
I computed ICCs using the Two-way mixed-consistency approach, and I plan on reporting the single measures, which could reflect the amount of between-subject variability considering a single time point. Their approach is somewhat different, as they computed both within and between subject variability using traditional ANOVA procedures and caculated the ratio between BS var and BS+WS var…
I’ll try that and see how well the results concur with the 2way-mixed approach.
ICC is calculated from the results of ANOVA. A two-way mixed effects model just means that raters are entered as a fixed-effects variable, whereas the items are entered as a random-effects variables. At that point, you can just use the formulas in Shrout & Fleiss to make the ICC(3,1) calculation, and use the Spearman-Brown prophecy formula to scale up to ICC(3,k) if needed. I am not sure who your “fixed raters” and “random items” are in this context though.
Dear Dr. Landers,
thanks a lot for your explanation on the ICC. I still have a few questions though.
In my study, I have two groups, a clinical and a control group, who have to fill in a questionnaire which consists of 30 items. Each group consists of 2 subgroups. In the first subgroup are parents (48 clinical group / 100 control group) and in the second subgroup are students (43 clinical group / 70 control group).
I’d like to calculate the ICC for EACH item and compare them between the clinical and the control group; e.g., compare the ICC of the rater agreement between parents and students of item 1 of the clinical group with the ICC of item 1 of the control group.
Is it possible to first calculate a mean/median of the parents’ and the students’ ratings per item, and then calculate the ICC using the One-Way Random-Model?
And how can I calculate the ICC for each item instead across all items? Can I split my dataset between the items or do I have to create a dataset (separate SAV files) for each item?
Thanks a lot in advance!
You can calculate ICC for any subgroup you want; you’ll just need to set up variables indicating each subgroup/variable combination you are interested in. You calculate ICC for individual items the same way – you just need one column for each rater/item combination (instead of rater/scale combination). I will warn you, however, that comparing item reliabilities can be dangerous, because item reliabilities follows a normal distribution just like any other statistic – and because you are looking one item instead of many items, the familywise error rate is dramatically inflated – so just because one item has a high ICC and another has a low ICC does not mean that either item is “better.” To make such conclusions, you’d need to compare Bonferroni-corrected confidence intervals.
Thank you for your quick response! For my study, it’s not so important to decide between “good” and “bad” items but to see if the rater agreement between the clinical and the control group is similar.
I’m not sure, if I understand your comment correctly. I tried to calculate the ICC for an individual item by putting the median of the parents’ ratings and the median of the students’ ratings in the item field and then pressed the statistics button, chose the intraclass correlation coefficient and selected the one-way random model. Instead of the results, I get the warning message “There are too few cases (N = 1) for the analysis. Execution of this command stops.”
Ah – I see. You don’t need item comparisons then – but you would still want to look for overlapping confidence intervals on your scale measures.
There are several red flags in what you’re saying. One, I’m thinking you’re using median ratings because your scale is not interval or ratio measurement, but this is a requirement of ICC. Means must be meaningful. If you are using ordinal scales, you can’t use ICC at all.
If you are in fact using interval or ratio scales, you should not calculate medians yourself as input to ICC – they should be means, and you should have 1 mean per rater per rating target (e.g., for 2 raters across 10 cases, you would have 20 scale means). Your cases must be independently drawn from some population of things (or people, or whatever) to be rated.
For ICC to make sense in this context, my mental model is that you have multiple parents and multiple students rating the same paper people. All of those paper people being rated (your N) must be on separate rows. If you only have 1 observation per case, it is impossible to calculate inter-rater reliability – so if you have only 1 parent and 1 student per rating target (or if you only have 1 rating target; for example, only 1 paper person), you cannot examine inter-rater reliability within parents (or within students) – it is impossible given that structure of data.
The main exception to this would be if the items on your survey are theoretical random draws from a population of items (e.g., if your items are really each themselves “paper people”). In that case, you really have one item per case (i.e., SPSS row). In that case, you would put all of your student raters as columns, and all of the items as cases, then calculate ICC; then repeat with parents; then compare confidence intervals (and raw effect sizes, of course).
That’s about all I can think of. You might want to bring a psychometrician in to work on your project – someone who can dig into your dataset would be able to give you more targeted advice.
Hi Dr. Landers,
Thank you for taking the time to write and follow-up on this blog post. It’s been very helpful.
In our study, we have ratings by four different raters but only one rater per case (n = 30-40). We had intended to have all raters rate one case to make sure the raters’ assessments were close together and then analyze this using an ICC but seeing as it won’t work with a sample size of 1, we’re trying to determine what to do.
While it’s not possible to have the four raters complete assessments for each individual in the study, if all four raters completed ratings for a small group of the participants (maybe 10%), would this be sufficient for determining the inter-rater reliability?
It depends what you mean by “sufficient.” It will allow you to calculate an estimate of ICC across your sample – rather than the actual ICC – which is better than nothing but still not perfect. But it will be inaccurate to whatever degree sampling error is a problem in the random raters you end up choosing. It sounds like you want to keep each rater completing only 3-4 additional ratings. That is not nearly enough to get a stable estimate. I would instead ask each rater to rate a second person (chosen at random). That would require each rater to complete 8-10 additional ratings. You could then calculate ICC(2,1) to get a stable estimate of reliability for your individual raters. You could alternatively do half of this (4-5 additional ratings each; getting 1 additional rating on half of your sample), but this is a little risky for the reasons outlined above. I wouldn’t do less than that.
Dear Dr. Landers,
this article really has proven to be a huge help for my evaluation, thank you very much for the clear and precise words on how to use the ICC.
I’m having a problem with my results though and hope that you might be able to give me a hint as to if there even is an issue and if so why.
I have 2 raters and 27 ratees. The data had to be coded into a scale with 7 categories so that every rater now has a value between 1-7 in each of his 27 rows. When looking at the data you can already see that most values only range from 4-5 and both raters seem to even concord most of the time so there seems to be very little variation but as soon as I let SPSS actually compute the ICC I only get a 0,173 as the result which is pretty low for data that seems to be so similar.
Should I just accept the low value as the correct result or did I do something wrong?
I actually counted how often both raters don’t agree and it’s 6 times but only marginally e.g Rater 1: 4 Rater 2: 5
Thank you for your help!
Kind regards,
Moritz
P.S. English is not my native language so should anything be incomprehensible to you I would be glad to try to give you a better explanation.
You are likely getting a low ICC because of low variance in ratings. If every answer is a 4 or 5, then that means for 6 cases out of 27 (22%), you have zero agreement. Zero agreement is very different from 100% agreement, so ICC is being dramatically suppressed. If possible, I’d suggest re-anchoring the rating scale and re-rating all of the cases with your new scale. For example, you might add more numbers with labels between 4 and 5. If that’s not an option, you might report simple percentage agreement instead (78%), which isn’t as rigorous an examination of agreement, but it probably more closely represents agreement in your sample.
Thank you very much, that sounds like I finally can move along since this has been bugging me for days without finding a solution to that odd result.
Re-achoring won’t really work I guess since the rating described above is based on the same scale I am also using for another Item but the ratings have a much higher variance there. That’s why the example with the 4’s and 5’s is basically an exception.
Is there something like an approximate variance that should be present to effectively compute ICC’s?
Thanks again for your quick response, it’s rare that someone answers questions so patiently.
There aren’t any rules of thumb, I’m afraid. The general idea behind ICC is that it looks at how much raters vary from each other in relation to how much ratees vary from each other. So if those proportions are similar, you’re going to have a low ICC.
What you want is low inter-rater variance and high inter-ratee variance to demonstrate high agreement. In classical test theory, your scale should be designed this way in the first place – you want to maximize the differences between people (so that your scale mean is near the middle, e.g. 3 on a 5-point scale, with a normal distribution reaching out to 1 and 5, and without ceiling or floor effects) in order to explain those differences with other variables.
Another way to look at it is in terms of scale of measurement. Because your raters are only using 2 options on the scale, you have converted an interval or ratio level measure to a nominal one. That will certainly attenuate ICC.
Dear Dr. Landers,
I am conducting ICC for a scale to determine reliability but I am having an issue when trying to examine the reliability for one item. I can run the analysis for the scale as a whole, or two plus items, but when I try to input one item, I receive a warning in SPSS output saying there are too few cases, n=1. Do you know if it is possible to calculate the agreement between raters for individual items? I have 40 raters and would ideally like to calculate the reliability for each item of my scale.
Many thanks for any help and for your explanation.
Best wishes,
Adele
If you’re getting an error about n=1, you’re either not running the ICC calculation correctly or you don’t have more than 1 ratee (which is required to model variance among ratees). You can certainly calculate ICC for each item, if that is meaningful (although it usually isn’t, for reasons I’ve described in previous comments).
Dear Dr. Landers,
thanks for taking your time to write the article and anwer people’s questions on this page.
In our study, we want to compare the ICCs (one-way random) between two clinical samples.
Clinical sample A and B, both consist of an adult rater (who are actually more adults, who each rated a different patient who belongs to the same group, and are therefore placed in the “adult rater group”) and a student rater (who also consists of more students who belong to the “student rater group”) who rated patients on a questionnaire.
In a first step, the ICC for each item of the questionnaire for clinical sample A will be calculated and in a second step, the same method will be used for clinical sample B. This procedure will then be repeated for 3 different groups.
I’m unsure if I should use SINGLE or AVERAGE MEASURES in order to make basic assumption about the ICCs between clinical sample A and B. But also if I have more groups, and want to compare the agreement between different groups (e.g.: how does the ICC of a certain item for the adult rater group 1 and the student rater group differ from the ICC of the same item for the adult rater group 2 and the student rater group, or to the ICC of the same item for the adult rater group 1 and the adult rater group 2) within a clinical sample. Do I have to use single measures or is it also possible to compare average measures?
Although I’d like to help, I am not at all understanding your design. This sounds like a very unusual application of ICC, and reliability in general. My inclination is that you’d want to compare average measures since there is no meaningful single measure unit (i.e. your “single measure” is some ambiguous half student-half adult hybrid rater and is thus uninterpretable). But your conclusions about ICC comparisons will be limited to student/adult combinations regardless, so I’m not seeing why you’d want to do this in the first place.
Hi Dr. Landers,
This is one of the most useful statistics articles I’ve ever seen. I wanted to know if I could please ask your opinion. My colleague and I conducted an experiment in which we could use some advice, if you have time. He taught 4 classes on 2 occasions and I taught a different group of 4 classes on 2 occasions. I was the experimental group and taught all my sessions with a game. He was the control group and didn’t use games. We each gave students a pre-test at the beginning of the first session and a post-test at the end of the second class.
Our hypothesis is that students in the experimental (games) classes performed better on the post-test than the control. Unfortunately we didn’t think to assign each student a number so that we could figure out which pre and post-test belonged to who. So basically we have a ton of pre and post-tests divided by class but not by student. Is there a a way we could conduct statistical analyses for the groups instead of individuals to see if our hypothesis was concerned?
Thanks so much,
Kate
This is a bit outside the scope of this article, and I’m not an ANOVA expert. But as far as I know, there is not really anything you can do as far as recovering the pre-tests goes. Assuming you were wanting to use pre-tests as a control variable in some sort of parametric analysis (e.g. ANCOVA), the basic idea is that the relationship between each person’s post-test scores and the covariate (pre-test) is determined first using regression, and then the variance explained in the post-tests from that regression is removed from the ANOVA model (creating what is referred to as the Corrected Model). Without the covariate-posttest link, you have no way to do that correction.
However, covariates do not necessarily need to be pre-tests. Although that’s generally best – and least error prone – you can also use anything you believe to be correlated with the pre-test. If you think that differences across classes in student achievement is the primary driver of pre-test differences in your DV, for example, you could just control for prior student achievement (using, for example, other test scores unrelated to the game – assuming you had the same tests in the two classes – or even prior GPA).
The last resort is to just assume that the classes were more-or-less equivalent ahead of time. Most research methods textbooks call that kind of design “generally uninterpretable”, but despite that is surprisingly common in education research.
Hi Dr. Landers,
This is really useful, thanks so much for your input. I really appreciate it.
Best,
Kate
Hi Dr. Landers,
I am conducting a research to measure the inter- and intra-reliability of subjects in preparing three different thicknesses of liquids (i.e. mild, moderate, & extreme). In this study, 18 subjects are required to prepare each thickness of liquid three times (e.g. 3 mildly thick, 3 moderately thich & 3 extremely thick). The thicknesses will be measured in centimeter but it can also be categorized into mild, moderate & extreme. May I know if I can use intra-class correlation to analyze the inter-reliability of subjects?
Thank you.
Best wishes,
Bing
You can use ICC on any distance measurement (like cm), since that is ratio-level measurement.
Dear Dr. Landers,
Thank you for your reply.
Sorry, I have another question here. Is it correct to analyze the data separately?
Can I use ICC(1) to measure the intra-reliability among subjects?
Thank you so much.
Best wishes,
Bing
I’m not sure what you mean by “separately.” You can use ICC(1) any time you want to assess the degree of consistency or agreement between multiple raters making ratings on the same targets. ICC is sometimes used differently in non-social-science contexts, which seems to be the context you’re talking about, and which I know less about; you will probably want to find a journal in your field that has done this and use that as an example for which specific procedures to follow.
Sorry for being unclear. I’m trying to ask if I need to analyze the data for 3 times to get 3 ICC values (i.e. mild, moderate & extreme).
I’ve posted my question online and would greatly appreciate if you can give me some suggestions.
Thank you.
http://stats.stackexchange.com/questions/92713/inter-and-intra-reliability-intraclass-correlation
Best wishes,
Bing
So, you haven’t described this very well, but based on your post on StackExchange and what you’ve said here, this is how I understand it: you’ve asked nine people to make nine solutions each – three replications within each type, which is actually a within-subjects condition assignment. I don’t know what your research goals are, but your design does not sound like a reliability study. It sounds like you are interested in between-person consistency – which is reliability – but also differences between solutions – which is not reliability. I’m not at all familiar with your field, so I have no idea what research question you could even be asking here. I think you are going to need to bring in a statistician (or at least someone within your field) onto your project to help you on this one – I don’t think I can do much more for you.
Hi Dr. Landers,
Thank you so much for this overview, it is very helpful! I would really appreciate your opinion on a specific example that I’m working with, if you have the time. For our research, we asked staff across 40 different schools to rate their school across a variety of dimensions. We are planning on identifying the highest and lowest performing schools based on these ratings. For each school, we have between 4 to 10 different professionals rating their school on 4 survey scales. We want to know if the professionals within each school rate their school similarly to the other professionals within that school (for each of these scales), so we really only have one case for each group of raters (the individual school). Is the ICC the appropriate statistic to examine this?
Thank you for your time,
Nicole
Yes, it is. However, you won’t be able to use the ICC tool in SPSS to calculate it because you have variable raters. You will need to either !) calculate ANOVA instead and calculate ICC by hand from the output or 2) use hierarchical linear modeling, which usually spits out an ICC(1,1) by default.
Thank you for such a quick response to my question. I really appreciate your help!
Dear Dr Landers,
It is very refreshing to have the seemingly incomprehensible world of statistics explained so well, thank you so much!
I have looked through the many posts on this page, but would like, if you have the time, to just clarify something for my own research.
Without boring you too much, I am looking at applying a specific technology in a new way, and my first step is to see whether I get reliable results. The research is in its pilot stages, so I am the only “rater” so far and I took measures from my participants at the same time, every day, for 5 days to see how reliable my measures are.
I have run an ICC on this data using a “Two way mixed” design and I have analysed for absolute agreement.
I have seen differing answers as to whether I should report the single measures or average measures output from SPSS? I was wondering what your advice might be?
Many thanks and kindest regards
Catherine
Well… first of all, since you’re holding raters constant (because it is just you) and varying time, you’re really calculating a variant on test re-test reliability instead of inter-rater reliability. So that affects the sorts of conclusions you can draw here. You are really only examining the reliability of yourself making ratings over time. You can’t speak to the reliability of anyone else’s use of this scale, as you could with an inter-rater ICC.
Also note that if you would expect true score variation over time (e.g. if the scores from you scale reflect real underlying change in your technology, or whatever it is that you’re rating), then you shouldn’t use ICC this way.
As for the single vs. average measures, it depends what you want to do with your data. If you’re comfortable with only a test re-test reliability estimate, and you want to draw conclusions from some statistics calculated upon the mean of your 5 days, then you want average measures. If you are trying to figure out “if I was to make one rating on one day using this scale, how reliable would that rating be?”, you would want single measures. Given your description of this as a pilot study for a technology you developed, I suspect you want single measures (since I’m thinking 5 days is an arbitrary number of days).
Dear Dr Landers,
A huge thank you for your very swift and thorough response, it really is very much appreciated.
I will go back to the analysis with some fresh eyes and work on test-retest reliability for now.
Thank you once again
Catherine
Dear Dr. Landers,
I have 40 raters who are using a 100 point scale to rate 30 speech samples. Someone suggested I use Cronbach’s alpha . I thought that technique was not appropriate for this dataset. I thought ICC would be appropriate? Is that right?
Thank you.
Well, you can technically think of alpha as a specific type of ICC.
To conceptualize the relationship between the two, you can think of your raters as items. The trade-off is that you lose a lot of the specificity that ICC allows, because alpha makes a lot of assumptions about items.
So for example, alpha is always consistency-based (not agreement), and I’d imagine that agreement is important for speech sample ratings. Alpha also gives you the reliability of your scale assuming you continue using all of the items, and it requires that you have the fixed number of items for each case. I believe alpha also assumes a fixed item pool (don’t quote me on that last bit though). All of those restrictions together makes it equivalent to ICC(3,k) for consistency. So if your data don’t match any of those assumptions, i.e., if you wouldn’t use an ICC(3,k) for consistency, alpha would not be appropriate.
Dear Dr Landers,
Thank you for your excellent explanation. I still have one question, though, that I haven’t been able to find the answer to yet: are there any reference values as to what constitutes a high, medium, or low ICC (I’m particularly interested in the 2,k/consistency model)?
I’m in the process of developing a scale. I wrote a pool of statements that I want to assess in terms of their content validity. To do so, I’ve asked 6 judges (experts in the field) to rate each statement on a scale of 1 to 5, 1 being “statement does not represent underlying construct at all” and 5 “statement represents underlying construct very well”.
To report on the judges’ reliability, I am thinking of using the ICC. From your information I gather that the ICC(2, k) (i.e., (2, 6)) model is the one to go with (type: consistency) (is this assumption correct?). But when can I label such an ICC as high (or medium, or low)? Do you know of any reference values (and/or perhaps a source I could consult/quote)?
Any advice would be much appreciated!
Sean
Well… two issues here. First, ICC is simply a type of reliability, so any standard for reliability you normally find sufficient is the same here. The classic reference (Nunnally) suggests 0.7 as an absolute minimum (i.e. 49% of the observed variance is “real”), but it’s a very loose standard and usually misinterpreted. See http://wweb.uta.edu/management/marcusbutts/articles/LanceButtsMichels.ORM.2006.pdf
Second, the reliability of the judges has nothing to do with the reliability of your scale, so I’m not sure why you want to know it. ICC(2,1) would tell you how much true score variance in judgment, on average, does each judge capture? ICC(2,6) would tell you how much true score variance the mean judge score contains. Either way, I think you’d want absolute agreement, not consistency – because you want to know “do judges actually agree on their ratings?”, not “do judges have similar patterns of agreement?”
Dr. Landers, Thank you for your quick reply. Yes, I saw Alpha as specific ICC type; that is why I wanted to get your take. I thought the individual samples were the items. Each rater rates 30 samples. The ratings will not be combined. Since, I’m using a sample of raters, I can use ICC(2)?
-Steve
Hi Dr. Landers, You’ve expanded my mind 😉 Raters are items and should appear in the columns of my SPSS dataset, while the speech samples are in the rows. Thank you! -Steve
You’ve got it! Glad to help.
Thank you for your swift reply!
I’m aware that ICC has nothing to do with the reliability of the scale as such. Based on the judges’ ratings I will select the ‘best’ statements (based on their mean score and SE), after which the scale will be piloted. Follow-up procedures such as confirmatory factor analysis and Cronbach’s alpha will then be used to determine validity (unidimensionality) and reliability respectively.
I just thought it would be helpful to calculate the ICC on the judges’ ratings as a measure of their reliability. Just suppose their answers are all over the place, and there’s little consistency (or agreement), then obviously something’s wrong with the statements (or with the selection of judges).
You mentioned that absolute agreement would be preferable over consistency for this type of application. Could you explain that? I’m using the ICC (I think) to find out whether the judges are consistent in their ratings (5-item Likert type scale). Suppose the following situation: one or two of the judges are of the strict type, and they consistently feel that a 5 is too high a score in any case (‘There’s always room for improvement’, you know the type…). But their rating patterns would be consistent with other less strict judges, wouldn’t ‘absolute agreement’ ICC then give a distorted picture?
I’m really in your take on this.
Thanks
Sean
Ah, I see. I guess I am surprised because typically content validity is decided by consensus judgment – the addition of reliability estimates at that stage doesn’t add much (IMO) because you are going to collect psychometric validation evidence later anyway. I suppose it doesn’t hurt though.
I was thinking absolute agreement because of your scale: up to “statement represents underlying construct very well”. If one judge rates “very well” and another rates “moderate” but their rating patterns are similar, you’d make the conclusion of high consistency in the presence of low agreement. I’d think you want a mean of “4” (for example) to be interpreted as all judges being equally approving, i.e. that “well” always means “well.” But if you think (and can argue in your writeup) that this is a situation where individual judges could be “strict” in making such judgments, then consistency is the better choice.
Of course, the progressive way to go about this would be to calculate both and see if they agree. If they do agree, no problem. If they don’t, figure out if it really is a by-judge severity effect (what you are arguing) or something else.
Thank you very much for your feedback. I’m definitely going to calculate both, and screen the data thoroughly to see what is going on exactly.
Hello Dr. Landers,
Your post has been increadibly helpful for me! However, I still have some doubts ans was hoping you might have the answer. I need to calculate the interrater reliability on a checklist assessing frailty using a dichotomous scale (yes-no answers). A total of 40 patients have been included and each patient was seen by 2 of 3 possible raters.
I am not sure If I should use a one-way or two-way random ICC and if I should I caculate icc per item or on the total score of the checklist?
Also, when performing the one-way (and two-way) ICC in SPSS, I get an error saying my N=0. Could this be due to the fact not all three raters assessed all 40 patients?
Any help would be much appreciated!
-Eveline
If each was seen by 2 of 3 possible raters, you don’t have a consistent rater effect, which means you need ICC(1).
If you want to use ICC, you should do it on either the mean score of the checklist, using 0 and 1 as “no” and “yes”, or on the sum. If you want to analyze individual questions, I would not use ICC – your estimates will be biased downward pretty badly.
In SPSS, you’re going to want only 2 columns of rater data associated with each case. You should not leave the data in the original 3-column format, or SPSS will assume you have missing data (which you don’t, based upon your design). So you’ll need to collapse your 3 raters into “first rating” and “second rating” columns, so that every case has exactly 2 ratings in exactly 2 columns.
Hi,
I have some likert scale questions, and a sample rating them. Each likert scale question have 5 items. How should I calculate inter rater agreement?
So far I saw that cronbach alpha is for item internal consistency, does this mean that it is not suitable for inter rater agreement and I should use ICC?
Thank you
If you just have a sample responding to scales about themselves (or their opinions), you don’t have raters as defined here.
Thank you very much for your quick reply! I’ve paired my data now so an ICC is calculated for each rater pair (A-B, A-C, B-C) on the sum score to avoid missing data.
I am writing a scale validation manuscript and the scale can be completed by either the patient or by an informant (usually a family member) on the patient’s behalf. The items are the same for whomever completes the form and so I would like to use both the patient and informant scores (n=4500+) in all analyses but I think I need to provide justification for this.
There are an additional 2700 patients who completed the scale themselves and also had an informant complete the scale, so each of these patients has two scores for the scale. If I were to perform an ICC with these patients’ two scores (comparing the scale total for the patients to the scale total for the informants) and return values of .4 or better (Shrout & Fleiss, 1979), could that be considered justification to use both the patient and informant scores (that I mentioned in the first paragraph) in the for the scale validation analyses?
For clarification purposes- I would only be using the 2700 patients’ data for the ICC purposes, not combining it with the other data set.
If this is something I can do, would the ICC be a one-way random with average measures? Is it inappropriate to use a two-way mixed model/consistency?
Thanks!
This is sort of a weird use of ICC. What you’re really doing with ICC is saying, “I have a sample of raters drawn from a population of raters – how well do they agree?” So by calculating ICC, you are already assuming that all of your raters come from the same population. If your ICC(1,k) is only .4, that means only 40% of the observed variance is true, which is quite low.
I don’t know your research literature, but the question I’d likely ask is, how do you know both sources are telling you the same information? How do you know that the quality of information isn’t better for one source versus the other? You lose any of that uniquely good information about a single rater source when you combine them.
If I were writing a paper, I’d conduct my analyses all three ways – using only informants, only patients, and with the average of both. If all three sets of analyses agree, then you have a strong case that rater source doesn’t really matter. If they don’t agree, you need to figure out why.
You definitely want ICC(1). ICC(2) requires identical raters, i.e. the same two people rating every case.
Hi Dr. Landers,
Your post are very useful for my research. Thanks a lot. but I have some questions here.
I’m doing multilevel analysis, which is to analyse students achievement in different schools. My data is consist of 2500 students in 92 schools. and I have 16 items in 4 variables.
To compute ICCs am I need to do on aggregated data for (each school) or on the every variables?
Thank you.
Since you have 4 variables you are presumably using in further analyses, you would calculate ICC for each of the 4 variables. If you’re looking at student ratings on their schools, you probably have different numbers of students per school. In that case, SPSS is not ideal for calculating ICC automatically, because it requires equal numbers of raters for each case. I would recommend instead calculating it by hand or by using a multilevel analysis program (like HLM).
Yes I am doing multilevel structural equation modelling. I’m done with conventional SEM and now work on multilevel analysis. I’m just calculate ICC by hand. Thank you for your advise. I really appreciate it.
Thanks.
Hi,
I’m so sorry if this has already been asked and answered, but should you report a negative ICC? I thought the value should be between 0-1, but certain packages such as SPSS can report an out of range ICC?
Many thanks!
Hi,
Perhaps you can share some insight. For intra-rater reliability, ICC and Cohen’s Kappa, I don’t know if these tests are testing the null hypothesis that the two measures are the same or are not the same. A minor technicality which makes a big difference. If an ICC comes back with a p<0.001 and a coefficient of 0.8, does that support that there is a statistically significant difference between measures?. Same question for Cohen's Kappa?
Richard
I’m not sure what you’re referring to with “these tests,” but if you mean the significance test being reported by SPSS, those are tests against a null of zero – they tell you that (for example), the coefficient alpha or ICC you observed is unlikely to have come from a population where the mean alpha/ICC was equal to 0. If you want to compare two ICCs to each other, you can do so by comparing their confidence intervals – if they do not overlap, they are statistically significantly different (unlikley to have been drawn from the same population, at least given the sample size you are using). However, it’s important to remember that statistical significance (or lack thereof) is insufficient evidence to conclude if two measures are “the same” or not. You would also need to investigate latent factor structure at a minimum, and preferably also explore the nomological net of each.
Thank you Professor Landers! Really good explanation on ICC for interrater agreement. Unfortunately I’m not too sure which ICC I should be using for comparison between twins. Hope you can help me out and point me in the right direction. Thank you very much!
Yi Ting
If you are talking about examining inter-twin reliability with twin pairs, all of your cases would involve unique sets of twins, which means there is no consistency between raters (you are assuming each twin is a randomly drawn rater from a population of twins), so you would use ICC(1).
Thanks for the reply! I have another question for you. I am under the impression that for ordinal data, that has not been assigned weights, an ICC is not an appropriate test for inter-rater reliability. Is this correct?
ICC relies on the normal distribution, which does not apply to ordinal data, so that is correct. You would most likely need some type of kappa.
Thank you! I’m now trying to figure out between using Weighted Kappa and simply Kappa. My data is not normally distributed and is ordinal. I’m comparing the inter-and intra-rater reliability of 3 different scales (similar to Likert scales but based on skeletal maturation in radiographs) based on three different locations (skull base, teeth and cervical spine). One structure is based on a 3 stage maturation, another location is based on a 4 stage maturation and the third location is based on a 6 stage maturation. The observations for the inter-rater reliability is done using the same methodology with only 1 other observer (Observer B). I had done Kappa measures for all 3, however, I was recently told that the 6-stage maturation has so many steps that it merits a weighted Kappa and that the others 2 indexs may not. I’d like your professional opinion! Thanks Richard (By the way, Great name)
I’m less familiar with kappa than ICC, and I don’t know anything about stages or maturation or whatever you field of study is… so I’m not sure how helpful I can be here.
I will say that weighting kappa is useful in any context where you have reason to claim that not all disagreements between ratings are equally indicative of overall disagreement. In nominal measurement, that doesn’t really come up (one person says “A”, the other says “B” – they disagree). But in ordinal measurement, it can be useful (if one person says “1st”, the other saying “2nd” agrees more than the one who says “3rd”).
I don’t really see any reason that the origin of data it is based upon makes a difference to the type of kappa you’d want to use, since all three of your measurements appear to be on the scale (at least if I’m understanding you correctly).
The primary downside to weighted kappa is that you need to create the weighting matrix yourself (or implicitly trust a computer program to decide on your weighting matrix for you, which I wouldn’t do). Then you need to quantify things like “how much worse is a 2-step disagreement than a 1-step disagreement?” which can involve a bit of guesswork. There may be standards for this these days in some contexts, but I don’t use kappa enough to know what they might be. It is simpler to just use kappa, but it is going to give you a more conservative estimate (because all disagreements are “100%” disagreements).
Thank you! That is very insightful and once agains hits the nail on the head for answering my question.
1) What are short comings of using Kappa in comparison to ICC
2) Do you know any indications to use more than one type of inter-rater reliability (i.e. ICC and Kappa)
3) I can’t seem to understand when to use Cronbach’s Alpha. Can you provide an example of when it would be appropriate to use?
Kind regards,
R
You might have better luck with a psychometrics course or textbook. I am really only scratching the surface here. 🙂
1) I don’t think the can be compared directly like that. If you have interval or ratio level data, you might consider ICC. If you have nominal or ordinal level data, you might consider kappa (or a variant – there are many). There’s no situation where you could use both that I can think of.
2) If you think you need to use more than one, you’re probably not using the right one. The basic concept of reliability is that you are capturing the percentage of observed variance that is “true”. You must choose a type of reliability that makes the right assumptions about what is allowed to vary and what isn’t. In the case of both ICC and kappa, you are assuming that raters don’t fluctuate over time, that raters are all drawn from the same population, and that the variations between raters is “error.” If those aren’t all true, you would want a different reliability estimate (sometimes requiring a different data collection method entirely).
3) That’s a complicated question, but it is most commonly used to assess the reliability of survey scales. Cortina (1993) can explain it better than I can: http://psychweb.psy.umt.edu/denis/datadecision/front/cortina_alpha.pdf
I have appreciated reading the discussion on ICC. I was wondering though, what if there is one consistent rater, and a series of other raters to confirm the reliability of this rater. Would this be calculated as ICC(2,1), ICC(3,1) or something else entirely?
Also would the variability of the data affect the calculation of ICC? The distances I am looking at getting consistent ratings on range from 0-1800 meters and plugging them into SPSS I get an ICC of 1.
Thank you!
Technically speaking, you don’t meet the requirements of any ICC; however, ICC(1) is commonly used in this situation. The reason is that ICC(1) assumes each rater is a random draw from a population of raters; since you may have a rater effect (if your consistent rater is lenient or harsh, for example), ICC(1) will probably be a conservative estimate of reliability.
If you are getting an ICC of 1, that implies you have 100% agreement, in which case you don’t need ICC. You can just report “there was 100% agreement”.
Hi Dr. Landers,
I hope you’re doing well. Thank you for your previous guidance with the ICC situation for my dissertation last year, it was very helpful. You may remember, I conducted an N=1 study where I administered therapy on a participant and was then rated by 2 raters on how well I adhered to the therapy manual. You’d told me I couldn’t use the ICC to describe the IRR between the 2 raters in that scenario because there was only 1 ratee, me. My dissertation chair disagreed, but that’s another story…
I have now completed a follow-up study which repeated the same N=1 design. I used the same adherence rating system, where I had 2 raters rate my adherence to the therapy manual again. I’m wondering how I can describe the IRR between the 2 raters in this study ? If I can’t use the ICC value because there’s only 1 ratee and 2 raters, then what test, if any, can I use to describe the IRR between the 2 raters?
Each rater rated the same 3/10 therapy sessions, chosen at random. Their ratings are here, in case it helps:
Rater 1 Rater 2
How adherent I was in Session 4 0.1875 adherent 0.22159
How adherent I was in Session 5 0.17045 0.21591
How adherent I was in Session 7 0.10227 0.15909
You can see Rater 1’s ratings are consistently 0.04 -0.05 units lower than Rater 2’s. Is that the only way I can describe their ratings, or is there another test I can use to formally describe their ratings (i.e., simple correlation) ? The only ratings data I have is what you see here.
Thank you so much,
Dave Juncos
Sorry, the formatting was off in my previous email. Here’s the ratings:
Rater 1
0.1875 adherence for Session 4
0.17045 adherent for Session 5
0.10227 adherent for Session 7
Rater 2
0.22159 adherence for Session 4
0.21591 adherence for Session 5
0.15909 adherence for Session 7
Dave
It’s not that you “can’t” use ICC with these sorts of data; rather, they don’t represent what you probably want them to represent. ICC with N=1 means that you can only generalize to yourself, because you are not a random sample of all possible rating targets. As long as the only question are you concerned about is how well you as an individual can be rated, there is no problem. But that is not really “inter-rater reliability” in the sense that most people would want to know it.
Adding raters doesn’t change this. You don’t have any variance in ratees; thus you violate the assumptions of all reliability tests if you are trying to generalize across other ratees. It is like measuring something at Time 1 and trying to generalize to Time 2. Yes, it _might_ generalize that way. But you have no way to make that claim statistically.
If you’re just interested in comparing raters, that is a different problem. For that, you need variance in raters. You could then use any type of statistical test whose assumptions you are comfortable with, but with N=2, that is somewhat dangerous in terms of the validity of your conclusions. In terms of alternative approaches, a correlation between raters would treat your raters as populations, with a sample of paired sessions. That may or may not be useful to you, interpretively.
Yes, that makes sense. If both raters are only rating me, then you can’t generalize their pattern of rating, i.e., how consistently or how randomly they rated me, to other ratees. I suppose if I’m only concerned with how well I can be rated, then this information is still useful. I guess it confirms the raters were rating me in a consistent way throughout their rating process. Which is useful because… it suggests they were paying attention throughout their ratings. I can’t think of how else that information is useful though.
But does it confirm I was adequately adhering to the manual? No. What I’ll need to do is simply ask my two raters for their subjective impression of my adherence to the manual. That will give me the information I need most.
You may’ve noticed, my adherence ratings were quite low (they ranged from .10227 to .22159). The problem is the adherence scale they used is too inclusive of ALL possible interventions for this particular therapy. Of course, it’s not possible to administer ALL types of therapeutic interventions from this therapy manual in EACH session. Rather, a good therapist will administer only a handful of interventions each session – they’re simply isn’t time to administer ALL types of interventions in just one session.
Thanks again for your helpful guidance! It’s always appreciated.
-Dave Juncos
Hi there,
I have most of the comments on your page so far and still have questions about whether ICC is appropriate for me or not.
I have had children rate 5 dimensions of their quality of life using a scale which on its own was deemed reliable for the population. Their parents then used the same scale to rate their children’s quality of life. Again, Chronbach’s alpha was good.
I am now using ICC to ascertain whether both children and parents were in agreement about their quality of life.
For each dimension I have entered each child’s and parents average score. I have run an ICC Two way random and absolute agreement (although I am still a little unsure if the two way random was correct)
In reading the average measures box most of the scores are ok but I have two ICCs which have come out as negative values. Am I right in just assuming there was very little agreement between parent and child over this dimension or have I made an incorrect assumption somewhere? Your advice is on this is hugely appreciated!!!
If you always have consistent child-parent pairs, I would probably just use a Pearson’s correlation for ease of interpretation. However, that only assesses consistency – so if you’re interested in absolute agreement, ICC is probably your best option.
You don’t have a consistent population of raters – you have a random sample of raters. So you should be using ICC(1).
ICC is not actually calculated as you would think a reliability estimate would be (i.e., by directly dividing true variance by observed variance). Instead, it estimates rater variance by subtracting the within rating target mean square from the between rating target mean square as the first step of its calculation. So if your within rating target mean square is larger than your between rating target mean square, you end up with negative values – that will occur when there is more variance within rating targets than between rating targets (which you could interpret as “very little agreement”).
In your case, it means that parents and their children differ from each other (on average) more than each child differs from the other children (on average).
Thank you so much for the speed of your response. In the case of the negative answer would I still report this or would I simply explain here about the between group difference being larger than the within group difference and not report the coefficient.
That depends on the standards of your field. If it were me, I would probably just report that the ICCs were negative and the implication (parents and children differ more from each other than children differ from other children on that scale).
Hi Dr. Landers, I have bought your book, “A step by step… but I can not find the part about “Computing Intraclass Correlations (ICC) as Estimates of Interrater Reliability in SPSS”. I would like to use your explanation about ICC and reliability as reference in my manuscript and I thought it was in your book. Have i missed that part or is it not included in the book? Thanks for the explanation on the website it’s realy great and you made me understand the analysis in SPSS and the theoretical background:).
Sincerely Charlotta
I’m afraid the book doesn’t have anything about ICC! It’s really just intended as a one-semester intro to stats at the undergrad level. This page is the only material on SPSS. I’ve thought about converting it into a journal article and expanding it a bit, but I haven’t done it yet!
Thank you soooooooooooooooooo much Dr. Really need this for my presentation next week! God bless.
Hi Dr. Landers,
I have a study that had 60 participants rate the content of 30 different articles. Each article was rated by 2 different participants (i.e., each participant rated only one article). The articles were rated on 4 questions, but I would like to use the mean of the 4 items. Am I correct to use ICC (1, 2)? And should my SPSS datafile have one column (the mean of the 4 items) and 60 rows (one for each rater)?
Thank you for your helpful article!
It’s definitely ICC(1), although whether you need the single or average measures depends on what you’re going to do with that number. Your data file would have two columns (rater 1 and rater 2), one line for each case (30 rows), consisting of two means (mean for rater 1, mean for rater 2).
That makes things very clear. Thank you!
I will be using the means for subsequent analyses, so I believe I am interested in consistency, and that is why I planned on using the means. Which I believe is ICC (1, 2).
If you want the reliability of the means because you are using them in subsequent analyses, that only implies you need ICC(1,2) instead of ICC(1,1). Consistency vs. agreement is a different issue.
Ah…my mistake, thank you for clarifying. Yes, that is what I am hoping to do. Thanks for your quick and clear responses! It was a great help!
Dear Richard,
thank you for your great resource and willingness to explain.
Would you please consider if my following reasoning is correct?
I have a sample of n raters. Each rater has to evaluate m products along q different aspects. As my goal is to evaluate if the detected “mean” value for each aspect and product is reliable, I have to understand whether raters have reached a sufficient level of inter-rater agreement.
So far, I (mis?)understood that I should apply ICC(2,k) on a n x m matrix of data, for each of the q aspects. If this is correct, which threshold I’d conventionally consider sufficient to say, “OK, the raters agreed upon”?
Would be equating ICC (average measures) to an agreement coefficient (like Krippendorf’s alpha) plainly wrong?
Symmetrically I could also calculate if the n raters agree on the q aspects for each of the m products. And probably this would make more sense.
I am sorry if my ideas are still a little bit confused: could you help me clarify them with respect to ICC and your valuabe resource? Thank you.
FC
That sounds right to me – SPSS-wise, you’d want n columns and m rows, replicating that approach for each q. That is inter-rater across-product agreement for each aspect, which is most likely what you want to know.
Flipping it so that you had n columns and q rows would give you inter-rater across-aspect agreement for each product. Q columns and m rows would give you inter-aspect across-product agreement for each rater. M rows and n columns would give you inter-product across-rater agreement for each aspect. Any of these (or any variation) might be useful information, depending on what specifically you want to know about.
There’s not really an agreed-upon “threshold”, but the level of reliability that is considered “enough” is going to vary pretty dramatically by field. I would say that the traditional reliability cutoffs – .7 or .8 – are generally “safe” as far as publishing is concerned. Below that, it’s going to vary a bit.
Thank you Richard, for the prompt and clear reply (I admire your diligence and availability). Your answer wrt the threshold opens a reflection that maybe has been already done here, in that case I apologize and accept reference to previous comments. You cited the traditional threshold for interrater agreement (from Krippendorf on): 70% and I don’t have reason to doubt this coud also apply to ICC, although I lack some knowledge to understand its plausibility: I trust you here. However the wikipedia page on ICC as means “in assessing conformity among observers” is pretty vague and avoids to speak of “agreement” (purposely?). It seems that such use of ICC would require observer exchangeability, which is a tough assumption to make, or verify through a test-retest or a two independent sample comparison. Moreover, if I really wanted to distinguish between inter-observer and intra-observer variability, as I want to detect the former one, I should focus on n raters and 1 case, which is a case where ICC is not applicable. Any comment on that would be highly welcome. Thank you very much.
It’s important to remember that .7 has been broadly interpreted as a critical threshold for reliability, and also to remember that all reliability is the same, given a particular measurement. Any given test and population (together) has only one true score reliability – however, the method by which you attempt to assess that reliability makes certain assumptions which may lead to its mismeasurement. So if you say “.7 is enough” for one type of reliability, you’re saying it for all of them. Personally, I would say that naming such thresholds is not meaningful, in general. It is only a shortcut, and sometimes, a harmful one.
Wikipedia is generally not a great source for specific details about statistics. ICC can be used for whatever you want to use it for. It can be used to assess either consistency or agreement, depending on which is meaningful in your situation. You would be much better off reviewing original sources.
You are correct that observer exchangeability is required for ICC(1) or ICC(2). These both assume a population of raters from which you have randomly sampled. In practice, that rarely happens. ICC(3) assumes a population of raters, which is more unusual and less useful conclusion-wise. In most cases, researchers have a convenience sample of raters and must assume they are essentially a random sample to meaningfully use ICC (or any other assessment of reliability). This is a necessary assumption given current assessment approaches in the social sciences.
If you want to assess intra-observer consistency, you should not focus on one case, because then you do not have a random sample of cases over which to assess that statistic. The reliability you obtained would be specific to that one case (a population), which is likely not the intended target when you calculated it.
My English teacher always said to me to avoid “the former” as a pronoun. Actually I was referring to INTER-observer consistency in my last comment. Thus, is your last passage related to that kind of consistency or to the INTRA-observer one? The rest is very clear to me, thank you again for the clarification.
I understood. My response is referring to both – only the last paragraph references intra-observer specifically, because you made an inaccurate statement about it (there is never a situation that I can imagine, intra- or inter-, where you would want to examine a single case – assessment of either requires multiple independent observations by each rater).
I also understood, thank you Richard. As a matter of fact, I said that also to evaluate the inter-rater agreement in 1 case (among n raters) would be interesting (if possible at all), but I admitted that ICC was not applicable. Maybe just the variance, or a Chi-square test on response uniformity could help, or some other measure of inter-rater agreement, but I should check their assumptions to see if they are applicable in such an extreme case. Thank you again!
Dr. Landers,
I would be appreciative if you could confirm that I am using the proper ICC. I have 200 video clips of preschool children interacting with their mothers. Each clip is rated from 1-7 on how compliant the child is (7 = more compliant). 132 of the clips are coded by a single rater (66 by Sarah and a different 66 by Pablo). The remaining 68 clips are coded by both Sarah and Pablo for purposes of assessing interrater reliability. As much as I appreciate their work, I consider my coders to be a random selection of available coders in the world. Clearly not all 200 clips are coded by both coders.
I believe I should use ICC(2, 1) or in SPSS lingo Two-way Random, single measure. It is single measure because when I ultimately analyze these data, such as by correlating child compliance scores with parenting measures, I will not use the average rating from my two coders (since 132 of my clips were not even coded by two coders). I will use a single rating for all 200 clips.
How does this sound to you? If it is correct, do you have any advice on how to pick which coder’s rating to use for the 68 clips where I have two coder’s ratings? Does randomly picking a coder for each of the 68 clips sound right?
THANK YOU!!!!
It’s important to remember that inter-rater reliability can only be determined with multiple raters. So the only cases from which you can determine ICC are the 68 for which you have two raters. So you don’t need to pick anything. On those clips, you are correct: you should calculate ICC(2,1).
But that number may not mean exactly what you think it means. Usually, we calculate ICC on our full sample In such cases, ICC(2,1) will be an estimate of the reliability of one rater across your sample, but you will only be calculating reliability on a subset of that sample. Thus you must assume that 1) those 68 cases differ only randomly from the remainder of your cases and 2) your raters varied in their rating processes between those 68 cases and the full sample only randomly. Hopefully you selected those 68 cases at random, since that is what you need in order to argue that using a subset doesn’t bias your reliability estimate (or any later stats), but it can be subtle. For example, if you had them rate the 68 cases first, you might have over-time biases (ratings may become more accurate with more practice).
Once you have ICC(2,1), you have a lower-bound estimate of reliability for the full sample if you calculate the means of your 68 cases and use those values as your estimates for those 68 cases alongside the 132 estimates you already have. Alternatively, you can randomly select one of the two coders for those 68 cases and use that, in which case you have an accurate estimate of reliability. But you will also be attenuating any later statistics you calculate (lower reliability means smaller correlations, smaller effects, etc). So I would use the means.
Dr. Landers. Thank you so much for your reply. To clarify, when I asked about picking coder ratings, I did not mean for calculating ICC. Clearly one needs two (or more) sets of ratings to calculate ICC. I meant for subsequent analysis between the variable that was initially used in an ICC and other variables. For example I might code compliance and subject it to ICC and then correlate compliance scores with measures of parenting.
Also, I would absolutely randomly pick which clips are coded by two raters to calculate ICC as I agree that there may be time or other effects.
With respect to your last paragraph. I was under the impression that if only a subset of my video clips were rated by two people, that lumping their average scores for those clips with the single scores of the clips only rated by one person would cause problems. You seem to be suggesting I do that since average scores by two raters are desirable. Is that right?
Finally, I guess Im confused by your statement that lumping the average scores of two raters with the single scores will produce a lower-bound estimate of reliability. Im not sure what you mean by lower bound. Are you also saying that randomly picking one of the two raters scores is more accurate? Than you so much again!
Assuming the assumptions of ICC are met, adding additional raters always increases reliability. Where you get into trouble (what I assume you mean by “problems”) is if those assumptions are not met, e.g., if your sample of raters are not a random draw of a population of raters. But in that case, you couldn’t use solo ratings either. The only situation where you might not use the means is if you had Rater 1 rate every case and Rater 2 rate a subset – in which case, you might just stick with Rater 1 for interpretive ease.
You can actually see the reliability of your mean scores by looking at ICC(2,2) in those analyses. It will be higher, and potentially much higher.
Thus, if you combine mean ratings and single ratings, your ICC(2,1) will be an underestimate of the reliability of your sample, which varies by case. But you will still get the effects of that increased reliability in subsequent analyses. Some types of analyses (like HLM) actually give you an overall estimate of reliability regardless of differences in the number of raters, but you need at least 2 raters for every case to do that (most useful when, for example, you have 3 to 5 raters of every case, which is common when studying small groups, teams, etc.).
I thought that the distinction between mean rating and single ratings was not about whether you have single or multiple raters, but about whether single scores from multiple raters or multiple scores (aggregated into a single score) from multiple raters are used to estimate interrater reliability using ICC.
The statistician, Andy Field writes:
So far we have talked about situations in which the measures we’ve used produce single values. However, it is possible that we might have measures that produce an average score. For example, we might get judges to rate paintings in a competition based on style, content, originality, and technical skill. For each judge, their ratings are averaged. The end result is still ratings from a set of judges, but these ratings are an average of many ratings.
Do I have that wrong? I guess Im having trouble mapping what you said about ICC(2, 1) and (2,2). Thanks again!
No, it is about what you want to generalize to, which is what Field is saying. Single measures is “what is the reliability of a single rater?” and average measures is “what is the reliability of the rater mean?” Functionally, when calculating ICC, you use ANOVA to determine the reliability of the rater mean and then use something akin to the Spearman-Brown prophecy formula to determine what that reliability would have been if you’d only had one rater. Once you know one, you know the other.
Last question. If you have 2 raters rate 50 video clips, then which rater (of the two) is the single measures referring to? Thanks!
Neither. You have determined the reliability of their mean rating and then mathematically adjusted that number down, under the assumption that both raters provide the same quality level of information.
Hi Dr. Landers
Greetings
I are currently analysing the relationship between employee performance (job stress) and customer evaluation of service encounter (service quality). I have collected information from employees of 10 different branches (no. of employees range 5 to 25 from each branch) and from customers of these 10 branches (no. of customers range from 10-60 from each branch). I am trying to providing the justification for aggregation of these two datasets to understanding the impact of job stress on customer perceived quality. Since customers interact with employees at the branch level, i wanted to justify aggregation at the branch level. However, i am not sure how to test the interrater agreement and reliabilities. How do we justify aggregation at the branch level? Thanks!
In the terminology of what I wrote above, you can look at ICC by considering each employee to be a “rater”, and each branch to be a target/case – multiple raters (employees) for each case (branch). But the implications and process of aggregation are a bit outside the scope of this particular discussion, primarily because the way you aggregate has theory-building implications. I’ve recommended a few sources elsewhere in this thread that might be helpful. If those don’t help, you’d probably be best off adding a collaborator on your project.
Dear Dr Landers,
Thank you for you very informative article. I am conducting a reliability and validity study and have a few questions that I could not draw definitive answers from the previous posts.
Reliability
I have 1 measure (leg angle) that is collected on 20 children. This measure is collected by one assessor on two occasions and another assessor on a single occasion. The assessors are only a sample from a population of assessors. From this data I want to calculate intra and inter rater reliability of assessors in performing the measure. My current method is as follows (base on my interpretation form the above post) for both intra and inter rater reliability:
Two-way random with absolute agreement and I interpret the Average measures ICC value.
Validity
I also have a ‘gold standard’ measurement of leg angle from MRI of the actual bones. How would you suggest I assess validity? Would I assess validity against a single assessor from one occasion or would I try to include all 3 assessments (i.e. 2 form one assessor and 1 from a further assessor).
Best regards,
Chris
You could do that. However, the intra-assessor number may not represent what you think it represents. If you look at two occasions for one assessor to assess intra-rater reliability, your estimate will only generalize to that one assessor. It [i]may[/i] generalize to other assessors, but you have no way to know that given that analysis. The only way to do that would be to have two or more assessors both rate over time.
For inter-assessor reliability, you would use what you’re saying (although it assumes your two assessors are a random sample of an assessor population).
For validity, since you have a measure without error (or nearly), you can assess validity in a very practical way – mean deviation across assessors from that error-less measurement, and the standard deviation of that deviation.
Hi Dr. Landers,
Thank you for this informative article. Please excuse my limited statistical knowledge as I still have some questions about our project. We have a group of 4 assessors conducting balance tests with study participants and we would like to be double check on our inter-rater reliability. We only planned to have more than 1 rater per assessment at the beginning of the study. Once we established that we have relatively good inter rater reliability, each assessor will then work on his/her own (as we can’t afford to have more than 1 assessor per session). Due to our schedule conflicts, for our 10 completed sessions, we don’t always have all 4 of us there (only one has all 4). However, each session had at least 2 raters (the combination is different each time). I believe that we should do one-way random (and we have a “population” rather than a “sample” – is this right? I am still quite confused between the 2 terms). However, when I ran the analysis in SPSS, it can’t generate any outputs as I only have one valid case (i.e., with all 4 ratings). How should I get around this?
One more questions, we are administering 6 different tests and each has various subtests ranging from 3 to 13. I understand that the ICCs should only be calculated with the “transformed” scores, and each subtest actually has its own transformed score. Is it necessary to calculate ICC for each subtest? Or, is it sufficient to calculate ICC only for the total score for each test?
Sorry for the lengthy post. Thank you for reading!
What you’re describing is a limitation of SPSS, not of ICC. The only way around it is to either 1) calculate ICC in a program that doesn’t have this limitation, such as HLM or R or 2) to calculate an ANOVA in SPSS and then calculate an ICC by hand using the output, based on the formulas provided by Shrout & Fleiss.
For your six different tests, it depends on what you want to know. If you want to know consistency by subtest, you’d need an ICC for each subtest. If you aren’t using subtest scores for anything (e.g., if you’re only using the overall test score in later analyses or for decision-making purposes), you don’t need them. You only need ICC for the means you’re going to end up using.
Dear Dr. Landers,
Thank you for your very prompt reply – much appreciated! I just realized that half of the tests are ordinal data, so I guess I am not really supposed to use ICC. Should I do kappa instead? For the crosstab analyses, I can only seem to compare 2 raters at once. Is this another limitation of SPSS?
Is there another resource that you can direct me to, so I can calculate the ICC by hand using ANOVA output in SPSS? Thank you very much!
Yes, kappa would be more appropriate for ordinal data. For kappa, there are actually several different types. Cohen’s kappa, which is what SPSS calculates, is for 2 raters only. You’ll want Fleiss’ kappa, which I believe you need to do by hand. More info here: Fleiss, J. L. (1971). Measuring nominal scale agreement among many raters. Psychological Bulletin, 76, 378–382.
For calculating ICC by hand, all of the formulas are contained in Shrout & Fleiss, which is referenced in the footnote of the article above.
Thank you for taking your time to answer my questions!
Thank you Rechard for your nice answers. I have one question. I want to aggrgete individual level data to organizational level. What statisitcs can I use to justify that such aggregations can represent organizational level construct? Thank you.
That is an enormously complicated question and has a significant theoretical component – in short, it depends on how you conceptualize “organizational level.” I’d recommend Johnson, Rosen & Chang (2011) in Journal of Business and Psychology as a starting point.
Hi Dr. Landers,
Thank you for this article, it’s very clear and now I know that ICCs aren’t what I need. But I’m hoping you can help me figure out what I do need! I have 2 raters each rating about 200 grant proposals on the types of strategies they are using to increase student retention. They had 19 possible strategies to choose from, and could apply as many strategies as they want for any given proposal (so, for example, Coder A may give proposal 1 codes 7, 8 & 4, whereas Coder B may give the same proposal the codes of 4, 8, and 1). These strategies are independent (i.e., not part of a scale) and nominal. Any ideas regarding how I would assess agreement for this type of scenario? I’ve figured I can dichotomize each strategy separately and calculate agreement between the two raters using Cohen’s kappa for each strategy individually (giving me 19 separate kappas, one for each strategy). But I was wondering: Is there a way to get agreement across all 19 strategies? Can you think of a better methods I should be using for this data?
If you have two coders consistently, determining inter-rater reliability for each of the 19 codes with Cohen’s kappa (matching “identified the code” or “did not identify the code”) is the right approach. I don’t know what you mean by “agreement across all 19” – you stated that the strategies were not part of a scale and were independent, and thus the “overall” agreement would not be a meaningful statistic. If you just want to know “on average, what is the reliability”, I would calculate just that – the mean Cohen’s kappa across your 19 scales. Reliabilities are proportions/percentages, so you can just calculate the “average reliability” if that’s what you want to know. But assuming you’re writing this up for publication somewhere (or an internal report, or whatever), you should still report all 19, since each code has its own validity, and differences in reliability/validity across codes is a meaningful concept given what you’ve described (if there is disagreement on one strategy but agreement on 18, this would be washed out in an average yet would be something important to know).
That makes sense, thank you so much Dr. Flanders!
Dear Dr. Landers,
This is a fabulous explanation of ICC and SPSS. Thank you so much! It’s especially helpful to me since my field, Library Science, does not use statistics & math as heavily as other fields. I have a question about the difference between “single measures” and “average measures” that appear in the output SPSS provides.
I’m currently conducting a rubric assessment to evaluation undergrad senior theses. Three librarians (2 colleagues and myself) scored an initial sample of 20 senior theses on 9 criteria measuring research and citation quality. The 9 rubric criteria were rated on a scale from 1 to 4. All three of us rated the same 20 projects on all 9 criteria, so I had SPSS calculate ICC for Two-Way Random, Absolute Agreement. I calculated ICC for each of the 9 criteria, but reading over your advice to Sofia, I also ran ICC on the total scores and average scores (i.e. I calculated created a sum total score and an average score for each senior project, for each rater).
My Question: Would I want to look at Average Measures or Single Measures? In our case, the average measures in SPSS look much more favorable (higher intraclass correlation) than the single measures.
Our hope with our initial testing of the rubric is to show an acceptable degree of inter-rater reliability (ICC of at least 0.7) so that we can move on to individually scoring a larger sample senior theses (much less time-consuming!). Thanks again for any light you can shed on this.
Darcy Gervasio,
Reference Librarian, Purchase College Library
If you’re interested in individually scoring the theses, you’re talking about the reliability of a single scorer (i.e., a single measure). If it makes you feel any better, the reliability of individual experts reviewing written student work (e.g., for course grades) is generally pretty terrible. That you’re paying attention to reliability at all puts you far ahead of most people doing this sort of thing.
The easiest way to develop a rubric with high reliability is to place objective criteria on it (e.g., number of citations). The more subjective it gets, the poorer your reliability is going to be.
If that’s not an option, unreliability in your case is going to stem from different mental models among the three of you about what each dimension of the rubric represents. You can also increase reliability by getting a unified mental model for each dimension among the three of you – the best way to do that is to do what’s called frame-of-reference training – identify the five or so papers where you had the greatest degree of disagreement, and then meet to talk about why your scores were different. In that discussion, try to come to a shared understanding/agreement of what score is the “right” score for each of those papers on each dimension. You should then find that your reliability goes up in a second sample of grading if you all commit to that mental model. And you might get it high enough to push that single measures reliability estimate up to a level you are comfortable with.
For the record, for “practical decisions” like grades, the reliability level recommended by Nunnally is 0.8 to 0.9. In practice, that’s obviously quite rare.
Thanks so much for your swift & helpful response! This clarifies a lot and reassures me about the “squishy” nature of grading and reliability. We have conducted one round of frame-of-referencing already on a smaller sample, but I will definitely try your suggestion of looking at the senior projects in this sample where we had the most disagreement. Unfortunately quantitative measures like raw number of citations don’t really get at the QUALITY of the citations (were they correctly formatted? did the student cite consistently?). It’s always tricky to conduct authentic assessments of written work and research skills since grading can be so subjective. Hopefully we can work towards unifying our mental model!
Even with subjective measures, you can usually get better reliability through one of two approaches.
One, you can often find room for a little more objectivity within a subjective measure. For example, correctly formatted citations as a single dimension seems highly objective to me – it only becomes subjective when you combine it with other less objective aspects of overall citation quality. A “consistent citation” dimension can be anchored – what does “highly consistent” mean and what’s an example? What does “moderately consistent” mean and what’s an example?
Two, ensure that your raters aren’t making their own priorities within dimensions. For example, if you have an overall “Citations” dimension, Rater 1 may think formatting is more important than consistency whereas Rater 2 may think the opposite. Even if they have the same judgments about the underlying aspects of “Citations”, that can result in disagreement regarding final scores. Chopping your dimensions up into finer pieces can help reduce that problem. But of course, it also adds more dimensions you’ll need to code!
Hi Dr Landers,
Firstly I’d like to say thanks for writing this, it is certainly more comprehensible than some other pieces I’ve read; however, I still have some residual confusion and wondered if you’d be kind enough to help please?
I’m trying to gauge reliability in decisions to include/exclude abstracts between 2 raters for a number of papers. The same raters rated all of the abstracts and data has been entered as either 1 (include) or 0 (exclude) into SPSS.
I believe I require ICC(2) but was unsure which specificity I require – ICC (2,2)? Therefore, analyse as: model as ‘two-way random’ and type as ‘absolute agreement’. Then read ‘single measures’ line.
Many thanks in advance!
Even if you can represent your outcome as 0 and 1, your outcome must be ratio-level measurement (i.e., can be conceptualized as 0% or 100% of something) in order to use ICC, and even in that case, ICC will be biased low because of the lack of data in the middle of the scale (e.g., no 50%). So I would not use ICC in this case, since your scale is not ratio. A better choice is Cohen’s kappa.
Thank you so much for your swift response!
To be honest, I was somewhat confused why I had been asked to do an ICC (by a supervisor) but assumed my confusion was because of my poor understanding. I feel far more comfortable with Cohen’s kappa. I really appreciate you taking the time to explain why.
Dear Richard
I enjoyed reading your content on the ICC and thanks a lot. Nevertheless, when I investigate test-retest reliability of a test that measure “Right Ear advantage” -a neuropsychologic variable- but rater is consistent in two sessions of testing, i should use two-way mixed model, Is that right?
If you have only one rater and always the same rater, I would actually just use a Pearson’s correlation. ICC assumes that your raters are a random sample of a population of raters; if you only have one rater making two ratings, you don’t meet those assumptions.
Greetings Dr. Landers,
I have read several of the questions in your assistance section and you likely have answered mine in the 130 plus pages, so my apologies for a redundant question. I created a global assessment measure for schools. This is a 1-100 scale that is broken into 10 deciles. Each decile includes terms to denote levels of student functioning in school. I contacted school personnel across the state and asked them to use the measure to score five vignettes. 64 of the school personnel met my criteria and rated EACH of the five vignettes. Thanks to your explanation, (and with hope that I understand it correctly, I am using a (2,2) as I consider this a sample of the larger population and look for consistency as I am coding for research. Across the top of my SPSS page, I have the 64 columns representing each rater, and my five rows representing the five student vignettes they scored. I ran the analysis and got a crazy high ICC (> .98), so I just wanted to make sure that this is set up correctly. Many thanks.
If you’re looking at average measures, that is actually ICC(2,64), not ICC(2,2). You have a high reliability because you essentially have a 64-item measure, which is a very high number of raters. If you always plan to have 64 people rate every vignette, or if you’re using that mean score as some sort of “standard” for a later purpose, then that’s the correct number. However, if you are in fact looking to use those numbers as standards later (e.g., if you’re planning to use the means you get from the 64 raters as an “official” number representing each vignette), just remember that high reliability 1) does not imply unidimensionality and 2) does not imply construct validity.
But Pearson’s correlation is not sensitive to systematic error. In my study rater has no effect because response of the patients is binary (Correct recall/Not correct recall). In test-retest reliability using ICC rater has replaced with trial. what is your opinion؟
Ahh, so that means you are not assessing inter-rater reliability – you are trying to assess inter-trial consistency. In that case, I am not sure which systematic error you’re concerned with – if you are concerned with error associated with each trial (your “raters”, in this case), you could use ICC(2). This would be most appropriate if the trials were different in some consistent way. If the trials are essentially random (e.g., if the two trials don’t differ in any particular recognizable way and are essentially random with regards to a population of trials), you should use ICC(1). However, you should remember that both of these assume one trial has no effect on the other trial; if they do, you’d still want to use Pearson’s.
The use of ICC further depends upon how you’re going to use the data. If you want to use average measures (e.g., ICC[1,2] or ICC[2,2]), your final rating will take one of three values: 100%, 50%, or 0% (the average number of successes across trials). If you need to use single measures so that all final scores are either “correct” or “not correct” you’d need ICC(1,1).
You might also consider use of binary comparison, which might be more appropriate given your data structure, like Phi coefficients or even chi-square.
Thanks for your response Dr. Landers,
I actually meant to report this as a single measure (I think). I want to be able to at some point have individuals use the instrument to assess baseline behavior and later use as a progress monitoring tool. Regarding the “crazy good” comment, I didn’t mean to infer that the measure is superior, I simply meant I didn’t expect to get such a high correlation and assumed I did something wrong. Many thanks. You are helping many of us and it is appreciated.
Yes, that is a correct application of single measures. I’m still not quite clear on your design, but if you got .98 for single measures, that is worryingly high – I would suspect inadequate variance in your sample of rating targets. 5 is not very many to believe you have a completely random selection of vignettes of all possible vignettes. You also want to ensure you have adequate variance in those scales – means should be toward the middle, and 2 SDs out on each vignette should still be well within the scale range. If you have floor or ceiling effects, that will also bias ICC.
So this may be the result of a poor design. I asked for multiple teachers to rate each of the 5 vignettes. I struggled to get teachers to complete the survey online, and to increase the number of variables would have likely resulted in even fewer participants. So would I have been better off to have FEWER teachers rate MORE vignettes? How is sample size calculated for a study like mine? Again thanks.
Yes, that would have been better. It is a balancing act though – ideally you want a large sample of rating targets and as many raters as you can get. You can actually get an estimate of how many raters you actually needed with the data you have – you would use the Spearman-Brown prophesy formula on ICC(2,1) to calculate a hypothetical ICC(2,k) in order to determine how many raters you would have needed for a stable estimate of ICC(2,1) – for example, with reliability = .8.
Conceptually, it’s easiest to think of raters as items, e.g., 5 people making a rating of one target is like a 5-item test. So you could use Spearman-Brown to determine how many people (items) you needed to get a target reliability across the whole scale, which is ICC(2,k) – you are essentially solving for k with a target reliability.
Your sample size is 5. There’s no calculation involved.
Dear Dr. Landers,
many thanks for your article, it is very clear and helpful!
I still have a question and I hope you can help me to understand better how to proceed.
I am developing a questionnaire to assess the awareness of a certain behavior. It will be probably a 20 item questionnaire (more or less) with a 5 point scale answer.
Each person will rate itself filling the questionnaire and for each person, two people who know him very well will also complete the questionnaire. I am interested to look at the inter-rater reliability so I was thinking to use an ICC (three raters: self-rating, rater 1 and rater 2).
How can I measure the sample size? What is the best number of ratee (self-raters)?
I was thinking to use a sample of 60 people but I need of a clear rationale to do that.
Many thanks,
Mia
That sounds like a situation for ICC. For what sample size you’ll need, it depends on what you want to do with it. If you’re taking the mean and using it some other stats, you need a power analysis, probably using a program like G*Power: http://www.gpower.hhu.de/
Dear Richard,
could you please elaborate on your comment on power analysis a little further? Do you mean that this kind of analysis can tell when it’s safe to use the mean and related parametric tests from ordinal values (assessments) because it can tell us if the effect is such that also non conservative techniques can be used, even if main assumptions are not met?
Thank you for your support and continuous help.
No, you’re referring to assumption checking.
Power analysis refers to procedures used to determine the appropriate sample size needed to reject a null hypothesis given a particular expected effect size and analytic approach. It is not something I can easily explain in a blog comment. I would suggest you start here: http://www.statsoft.com/Textbook/Power-Analysis
Sure Richard. It was just to understand for what you were suggesting the power analysis and your prompt reply answers my doubt already. As you possess a rare talent for clear explanation I hope in the future you ll treat more topics in statistics here (hypothesis testing, power analysis,…) as your blog would soon become a classic in popular (statistical) science… Best
Dr. Landers,
I am conducting something somewhat like a psychophysics experiment. I have numerous participants (50), who will provide ratings of 10 different variables, but they will do so 4 times each. Can ICC be used for INTRArater reliability? I understand it’s most common use is for interrater reliability but I am not exactly sure of which method to use for measuring how accurate each rater is across the four times they will rate the 10 variables.
Thanks very much for your help.
Sure. Just flip the matrix to whatever configuration you need. Just keep in mind what you’re assuming.
In ICC, you always have three sources of variance: case variance, which is expected to be random, systematic rater variance, which you only assess with ICC(2) and ICC(3), and unsystematic rater variance.
If you flip the matrix to examine intra-rater variance (cases as raters, raters as cases), you are changing this around a bit:
rater variance, which is expected to be random, systematic case variance, which you only assess with ICC(2) and ICC(3), and unsystematic case variance.
Note that this will not tell you how consistent individual raters are – instead, you’re only assessing intrarater reliability.
If what you’re really trying to do is identify “bad” raters, there is no set procedure to do that. But what I usually do is use the reliability analysis tool in SPSS with the “variance if item deleted” function to see if alpha reliability would increase dramatically if a particular rater was deleted – if that effect is consistent across rating targets, then that’s pretty good evidence that there’s something wrong with the rater. You can also look at rating distributions – sometimes for example you can see normal distributions for most raters but then severe skew for one.
Dear Dr. Landers,
many thanks for your help!
I will go through Gpower as you suggested.
Many thanks!!
Thank you sir, this is really of great help for me as i was unable to find any source to know how to calculate ICC(1), ICC(2) but now i understand how to calculate it. My research work deals with groups in public sector undertakings. I will be grateful to you if u also tell me how to calculate rwg(J)….to justify the aggregation of individual scores….or any link related to the process of calculation of rwg(J)..
I would suggest:
LeBreton, J. M. & Senter, J. L. (2008). Answers to 20 questions about interrater reliability and interrater agreement. Organizational Research Methods, 11, 815-822.
Also keep in mind that in the aggregation literature, ICC(1) refers to Shrout & Fleiss’ ICC(2,1) whereas ICC(2) refers to ICC(2,k).
Just FYI according to Bliese et al., (2000) ICC(1) = ICC(1,1) and ICC(2) = ICC(1,k).
Could you maybe tell me whether ICC is the appropriate method in the following situation, since I’m not entirely sure.
20 respondents of a questionnaire have been asked to evaluate the importance of a certain matter, on a scale from 0 to 10. 10 respondents belong to group A and the other 10 belong to group B. I want to determine how well respondents in group A agree on the importance of this matter in comparison to group B.
Thank you for your help!
That sounds like an independent-samples t-test to me.
Dear Dr. Landers,
Let me please give some additional information to my previous question. Both Group A and Group B consist of 10 experts, which are samples of the total population. When we add the experts from both groups together, we are consequently speaking of 20 experts in total.
Group A is asked to evaluate the importance of 30 factors/issues on a scale from 0 to 10.
Group B is also asked to evaluate the importance of the same 30 factors/issues.
Now I want to compare these groups with each other. Using Intraclass correlation I want to apply the “Average measures value” to indicate the degree of agreement among the rater groups A and B.
Could you tell me wheter ICC is the right test to determine the degree of agreement among groups in the first place? If not, which test can?
In addition I tried to incorporate the above in SPSS. For every factor/issue I run a separate ICC (1,2) test, so 30 tests in total. In the columns (2) I have put the rater groups: Rater group A and Rater group B. The rows (12) represent the expert measures.
Could you maybe explain me whether this is right?
Thanks in advance!
I’m not clear if your 30 factors are dimensions/scales or cases. If they are cases, I think this is still a t-test problem. If they are dimensions/scales, I’m not clear on what your cases are.
If you are treating them as cases, your 30 issues must be a random sample of all possible issues. If that’s not true, they are scales.
If they are scales, you need to have replication across scales, e.g., each expert in each group rates 20 cases on all 30 issues.
The design approach you are taking determines the analytic approach you would take moving forward.
Dear Dr. Landers
Thank you for this impressive website and your indefatigable work in teaching us statistics. I have a study where we measure lipids in two successive blood samples from a series of 20 patients. What I want to see is how reliable the measurements are for each lipid (some will be good, some not is my guess), i.e. do we get the same value in the second measurement as in the first. They are all analysed at the same time on the same machine. I know that the lipid levels are continuous measures, but they are not normally distributed (positive skew). Is the ICC(1) test appropriate? If so, should I report the single measures or average measures? Many thanks in advance.
ICC is based on ANOVA, so if assumptions of normality (or anything else from ANOVA) don’t hold, you can’t use ICC. There are a couple of possible approaches here. If you think that the data are normal with a positive skew, the easiest approach would be to use transformations to bring it back toward normality – most commonly recommended is a Box-Cox procedure. If your data are not in fact skewed positive and are actually a distribution that simply appears skewed – like a Poisson – then you shouldn’t do that. In that case, you might consider using a rank-order correlation, like Spearman’s. The downside to that approach is that Spearman’s assumes your measure ordering is meaningful – that the first measurement and second measurement are paired – so that could bias your estimate – and it also only gives you the reliability of a single measure – the equivalent of ICC(2,1) – which might not be what you want.
Beyond that, I’m out of ideas.
Many thanks for the speedy reply – much appreciated. I can the data to pass the D’Agostino and Pearson omnibus normality test when I use log10 values, so I guess I can use those, but I’ll have a crack at Box-Cox since you recommend that. That gets me back to the question about which ICC to use. I had a go and I seem to get the same result in SPSS regardless of the model – is that simply because I have only two measures per patient, rather than a single bunch?
If by models you’re talking about ICC(1) vs ICC(2)/ICC(3), you’ll see little difference between them when you don’t have consistent rater effects – that is essentially what ICC(2)/(3) “correct” for versus ICC(1). Since you’re just doing two random samples (there are no consistent raters), you would not expect a rater effect. If there is no anticipated rater effect (as you’d expect when ICC(1) is appropriate), ICC(2)’s calculation can take advantage of chance rater variation, which would bias ICC(2) upward. But that is why you should stick with ICC(1), even if the values end up being similar.
All the Box-Cox procedure does is allows you to see the effect of various lambdas (transformations expressed as data to the lambda power) to see which one approximates normality most closely. If you’ve already found another transformation that minimizes skew, it’s probably not going to make things much better.
Dear Dr Landers,
On your above comment you say that ICC is based on ANOVA and can therefore only be used on parametric data. I have been struggling to find a quote to this effect so was wondering if you might know of any references I can use to support this?
Many thanks
Catherine
I don’t know where you might find a “quote” to that effect, but Shrout and Fleiss talk to a great extent about the derivation of ICC from ANOVA. You might find a specific quote in there somewhere that meets your needs.
Hello Dr Landers,
I really enjoyed reading all the discussion about the best ways to use ICCs.
In my study I’m comparing the reliability of measures across three different instruments, and trying to infer recommendations on the most reliable one to be used in the population of interest.
The ICCs were all greater than .75, and the 95%CI all overlapped. However, the ICC point estimate of one instrument was not always contained within the 95%CI of the other.
Question:
Is it correct to infer that one ICC was significantly higher/lower than the other if the point estimate fell outside of the 95%CI, even though the CIs overlapped?
Any advice would be much appreciated.
Thanks you very much,
Gus
To conclude statistical significance definitively, the confidence intervals cannot overlap at all. However, if two intervals do overlap, I believe that the estimates could still be statistically significantly different, although it is unlikely. At least, that is my impression, since that is the way means work (i.e., for independent-samples t-tests). I’m actually not sure what sort of test would be best for the difference between two ICCs (that’s a very uncommon need, so there is not much literature), but I suspect it might be something like the test between two independent Pearson’s correlations. I’m not positive that the sampling distributions are the same though (for Pearson vs ICC), so don’t take that as a definitive recommendation.
Once again, many thanks – you a a great teacher. I will try to be a good student!
Things are moving on… In my samples I have the 18 cases who did two series of sampling on two separate occasions. Series A: sample – rest – sample. Series B: sample – intervention – sample. For series A, I get an ICC value of 0.63 with 95% confidence limits 0.27 – 0.84. For series B, I get an ICC value of -0.061, with 95% confidence limits -0.48 – 0.39. At first sight, it looks like the intervention affects the test-retest reliability, but that is describing “the difference of the significances”, whereas what I need to do is to measure “the significance of the difference”. The two values are for the same cases, randomised to do either A or B (or vice versa). The mean values do not change, and I don’t see an interaction term in a two-way repeated ANOVA, but you wouldn’t expect to if the intervention is changing the reliability of the measure in a random, rather than a directed, manner. Is there a neat way to compare my two ICC values? Many thanks in advance.
Examination of overlapping confidence intervals is the traditional way to determine if two independent point estimates are statistically significantly different. However, I am not sure of the procedure used for ICC, since that’s not a very common need, and I’m not aware of any research literature on it. In your case, to make this more complicated, you have a within-subjects design, so straight confidence interval comparison won’t actually work either, since that assumes the two ICCs are drawn from different samples. So I don’t have a recommendation I’m afraid. Let me know if you figure it out though!
Many thamks for the input. I’ll do my best!
I have collected questionnaire based data from around 100 firms. From each firm, a sample ranging between 5 to 30 individuals have responded. For study at the firm level, I intend to create a firm level score from their individual respondents. Which ICC do I need to calculate and report. And how do I calculate ICC and Rwg. I am using SPSS 20. for my research. Please help
Aggregation is more complex than reliability alone, but you generally need both 1) an estimate of how much an individual’s opinion reflects their group, which is ICC(1,1) and 2) an estimate of how much true score variance is captured by group means, which is ICC(1,k). If your groups range for 5 to 30, you’ll want to either calculate ICC manually using ANOVA and hand-computation or a program that does it for you, like HLM. I don’t know how off-hand to calculate rwg since I don’t do aggregation research, but I’ve cited a few articles in other comments that should help.
Dear Dr. Richard,
Thank you very much for the informative post. This is very useful because you have a real talent of explaining statistics to people who from non-statistical background.
I have computed ‘resilience level’ of 40 people using three different indices [i.e. methods]. In all three indices, resilience level has been computed as an aggregated value of a set of indicators (eg. age, sex, eye-sight, pulse rate). Indicators use in one method is not exactly similar to the other. I meant some indicators are common and some are different. Each index use a different method of computing the aggregate value [i.e.resilience level]. I wanted to see how identical the results obtained from three indices. For that I have calculated Pearson co-relation but it only compares two pairs. As I want to compare the relationship of all three, can I use ICC?
To make the question more clearer, I want to say how similar/distant the 3 resilience levels (of the same person) computed by 3 methods. (I have a sample of 40 people) Will ICC help for this?
Thanks in-advanced for any explanation you can give.
Chet
That’s not reliability, although it is a valid use of ICC. If the items are not identically scaled (e.g., all from 1 to 10), you would need the consistency type (not agreement). The problem, however, is that if there was disagreement, you would not be able to say which of your three indices was causing it. A correlation matrix would still tell you more.
Assuming all of your indices are on the same scale, and if all of your indicators are being used in some combination across your indices (i.e., if each index is made of the same indicators but in different combinations), I would think you’d want to use multiple regression to determine the ideal combination empirically based upon your criterion (whatever you’re trying to predict). If you don’t have a criterion, I would probably just use a 1-way ANOVA with post-hoc tests, defining each group of indices as a condition. Depends a bit on your specific RQs though.
Dear Richard,
Thank you very much for this post, i have read a lot around this topic, including the S&F article, but this was the clearest explanation I found. I don’t have a particular model to test but i am teaching this topic to PhD students and i would like to be entirely clear before doing so, so i have been simulating different analyses and reached a problem i can’t really make sense of. Any suggestions would be most helpful
In this case i have 3 raters (which as fictitious i considered that they could be a sample or the population) rating 8 ratees.
My problem is that regardless of using the RANDOM (which i think one should do if looking forICC 2,1, k) or the MIXED (for ICC 3, 1, k) options, i obtain the same results. In other words, these syntaxes give me the same results.
RELIABILITY
/VARIABLES=judge1 judge2 judge3
/SCALE(‘ALL VARIABLES’) ALL
/MODEL=ALPHA
/ICC=MODEL(RANDOM) TYPE(CONSISTENCY) CIN=95 TESTVAL=0.
RELIABILITY
/VARIABLES=judge1 judge2 judge3
/SCALE(‘ALL VARIABLES’) ALL
/MODEL=ALPHA
/ICC=MODEL(MIXED) TYPE(CONSISTENCY) CIN=95 TESTVAL=0.
When changing the option from CONSISTENCY to ABSOLUTE (agreement) the results are again the same for these two options (though different from the results obtained with the option CONSISTENCY)
RELIABILITY
/VARIABLES=judge1 judge2 judge3
/SCALE(‘ALL VARIABLES’) ALL
/MODEL=ALPHA
/ICC=MODEL(RANDOM) TYPE(ABSOLUTE) CIN=95 TESTVAL=0.
RELIABILITY
/VARIABLES=judge1 judge2 judge3
/SCALE(‘ALL VARIABLES’) ALL
/MODEL=ALPHA
/ICC=MODEL(MIXED) TYPE(ABSOLUTE) CIN=95 TESTVAL=0.
I ran the same dataset in an online calculator and the results I obtained with the option (ABSOLUTE) they report as ICC (2, 1, K) and the results I obtained with the options (CONSISTENCY appear reported as ICC (3,1,k). http://department.obg.cuhk.edu.hk/researchsupport/IntraClass_correlation.asp
I was confused with this, as I was expecting the results to differ as a consequence of random/mixed, and not just ABSOLUTE/CONSISTENCY. Does this make sense to you?
The other question is (I hope) simpler – what are the cut off points recommended for ICC (2, 1), ICC (2, k) and ICC (3, 1) ICC (3,K)
Thank you so much for your time and advice!
Claudia
Reporting of ICC is quite inconsistent, so I wouldn’t read much into the particular way anyone reports it unless they give the source they’re basing it on – that is why it is still to this day important to cite Shrout & Fleiss if reporting an ICC based upon Shrout & Fleiss. There are actually types of ICC beyond those of Shrout & Fleiss, so this is just one conceptualization – although it is one of the two most common.
Absolute vs. consistency agreement is not typically part of reporting in the Shrout and Fleiss approach, because Shrout and Fleiss were only interested in agreement. Their work was actually later extended by McGraw & Wong (1996) to include consistency estimates. When agreement is high, consistency and agreement versions will nearly agree, although agreement can be a little higher in certain circumstances. But you can make the difference more obvious in simulation if (for example) you add a large constant to all of the scores from one of the raters only. For example, if you’re simulating a 5-point Likert scale across 3 raters, add 20 to all scores from one rater. Your consistency ICC will stay exactly the same, whereas the agreement ICC will drop dramatically. In practice, you’re only going to see differences here when there are large mean differences between raters but similar rank orderings.
The difference between Shrout & Fleiss’ ICC(2) and ICC(3) is more subtle, although disagreement between them become large when agreement is poor but consistency is high.
Your question actually triggered me to hunt down the SPSS documentation on ICC, and it looks like they use the McGraw & Wong conceptualization, although many of McGraw & Wong’s versions of ICC are missing from SPSS. I also ran a few simulations myself and found that ICC(2) and ICC(3) in SPSS agree in situations where they do not agree when I analyze the same dataset in R using the ICC function of the “psych” package. So I’m at a bit of a loss here. There’s not enough detail in the SPSS documentation to be able to hunt down the reason. You can see the full extent of this SPSS documentation here: http://www-01.ibm.com/support/knowledgecenter/SSLVMB_22.0.0/com.ibm.spss.statistics.algorithms/alg_reliability_intraclass.htm
You can also see some discussion of how the SPSS calculations were incorrect for several previous versions of SPSS in the documentation for the R package – perhaps they are wrong again:
http://www.personality-project.org/r/psych/help/ICC.html
Dear Richard,
Thank you so much for your prompt and thorough response, and for the links for the SPSS materials, I will check them.
I went back to the data provided as an example by Shrout & Fleiss and ran it again in SPSS to check if I could replicate the results reported in their ICCs table by using the SPSS – ICC calculations.
Regarding the ICC (1,1,k ) and the SPSS one-way random the results are exactly the same.
I am able to obtain the results that S&F report for ICC (2,1,k) by selecting as type (ABSOLUTE), regardless of the model being random or mixed;
and i am able to reproduce the results that S&F report for ICC (3, 1, K) by selecting as type (CONSISTENCY), again regardless of the model being random or mixed.
So it seems to me that SPSS nomenclature is probably different than that used by S&F.
I am however not sure if i can assume that the pattern of results will be consistent for all cases I may with to test.
In any case, my best conclusion so far is if wishing to obtain ICC (2,1,k) i should use model: random (in case results change as agreement/consistence change, as you mention) type: agreement; and if wishing to obtain ICC (3, 1, k) one should use model: mixed; type: consistency.
Another – and possibly more trustworthy – option is to run the anovas with random/mixed effects according to the type of ICC required and calculate the formulas.
Again, thank you very much for your post insights on this, it was most helpful.
Claudia
Dear Richard,
That’s a very informative post. I have a query regarding the usage of cronbach’s alpha for scales with only two items. Is it appropriate to measure internal consistency using cronbach’s alpha for scales that have two items whose responses are rated on a five point likert scale. How does the number of items in a scale affect its cronbach’s alpha?
thanks in advance
santosh
As long as the standards of your field allow Likert-type scales to be treated as interval or ratio measurement, then sure. Some fields are more picky about that than others. The relationship between scale length and alpha is complicated – I’d suggest you take a look at the following article dedicated to exploring that idea:
Cortina, J. M. (1993). What is coefficient alpha? An examination of theory and applications. Journal of Applied Psychology, 78, 98-104.
thanks a lot Richards, will look into the source suggested by you
So if an ICC of 0.4 with a 95% CI of 0.37-0.44 – is this adequate inter-tester reliability?
Your assistance is greatly appreciated!
That depends on the standards of your field and what you’re doing with that number. If you are trying to assess the reliability of a mean that will be used in other analyses, that is pretty bad, generally. Inter-rater reliability is still reliability, so the traditional standards (e.g., Nunnally’s alpha = .7) still apply if you trust such traditions. However, there are many areas with lower standards of quality for measurement.
Hello Dr. Landers,
Do you provide any examples of the results write up for the ICC? I have ‘a two-way random effects, absolute agreement single measures ICC (2,1) .877. What exactly does this indicate?
Thanks in advance
I’m not quite sure what you mean by “results write up”, but assuming that’s a Shrout & Fleiss ICC, it means that 87.7% of the observed variance of a single rater is true variance (i.e., reflecting the construct jointly measured by the population of raters the rater is randomly drawn from) when considering mean differences between raters to be meaningful. You would just report it as ICC(2,1) = .877.
Thanks,
How do I cite you and this website (APA)?
It depends on what part you want to cite. I recommend checking this out for guidance: http://blog.apastyle.org/apastyle/2010/11/how-to-cite-something-you-found-on-a-website-in-apa-style.html
Dear Dr. Landers How many raters? (I know at least 2) or how many ratees? do I need to have power to determine the reliability of a classification scheme. Subjects are assessed for personality and are given a numerical classification of 0-24
Thanks Andrea
For how many raters, that depends upon what you want to know. If your goal is to produce a reliable mean score, it depends upon how reliable each person’s individual observations are, which depends upon your coding scheme, and what degree of reliability you are targeting. You can use prior literature to help guide that decision, and then the Spearman-Brown prophecy formula to figure out the specific number. For personality, my intuition is that you’d need 5 to 7 raters to reach a reliability of the mean rating of .7, but that will vary by personality trait.
For how many ratees, that depends upon how wide of a confidence interval you are willing to accept around ICC, and you can calculate a priori power based upon that model. For t-tests, which are similar, the typical rules of thumb more or less apply if you don’t want to bother with power calculations: at least 20 per measure. So if you end up needing 2 raters to get reliability, I’d get at least 40 people. If you need 6, I’d feel pretty safe with 100. More than 250 is probably enough regardless of how many raters you have, unless your single-measures ICC is exceptionally poor. The only way to be sure is to run through the power calcs for your particular situation.
Hi Dr. Landers,
I’m so happy I came across your site! I am a beginner to ICCs and this site has proved to be very valuable.
I have a question that I was hoping you could help me out on. I am involved in a study that is exploring the reliability of a situational judgment task (basically the development of a behavioral observation scale). The test is composed of 14 questions with scores ranging from 1-3 for each item. We had two independent raters code 69 tapes, with an overall average ICC of .804. The only thing I’m worried about is two of those 69 tapes produced negative ICCs (-0.182 and -0.083) and I’m wondering how those should be interpreted.
Through this thread I learned that these scores might be due to 1) a lack of variability (and you suggested the scale be reanchored to increase variability, but I don’t think that is possible at this point), 2) a small sample size and/or 3) near-perfect agreement. But I’m still wondering what to do with those values when writing up the manuscript. Should they just be forced to 0 since it only happens twice? Or does it even need to be mentioned due to the low baserate (only 2 tapes?) And if so, how would you recommend describing and reporting those values?
Thank you so much for your help, I really appreciate it!!
I would actually say that a rating 1-3 makes ICC somewhat inappropriate – that sounds like an ordinal/categorical scale to me, in which case I’d use a Cohen’s kappa or simple percentage agreement instead. The further you deviate from the assumptions behind ICC (i.e., normally distributed interval/ratio data), the less interpretable ICC will be. Have you checked if you have nice, clean normal distributions of the 14-question means or are they a bit lopsided?
Dr. Landers,
Thanks for the wonderful explanation! ICC is very confusing and I really appreciate this post! Nevertheless, I do have a question about my data: I have a repeated measure dataset with data for protocol compliance for 2 dozen participants over 6 observations using two types of criteria (one is the gold standard, the other one is the new method of measurement; both binary variables, compliance 1 or 0). I am interested in see how much in agreement the new method is to the gold standard, considering the within subject correlation (the idea being compliant participants are likely to be compliant in the subsequent observation, non-compliant participants are likely to be non-compliant later).
I’ve been told that I can use repeated measure kappa statistics, but I am not quite sure how to make the choice.
I’d really appreciate any of your suggestions and thank you so much in advance!!
Cheng
ICC, as considered by Shrout & Fleiss, isn’t appropriate for data captured over time. However, the more general case of ICC could be, although you’d need to either a program like HLM to model it (i.e., observations nested within time nested within person). But even if you did that, it would be non-optimal given the binary nature of your ratings. You also have a somewhat more difficult case because you have meaningful ordering – in statistical terms, your gold standard rater is not drawn from the same population as your experimental rater, so you know a priori that the assumptions of any reliability analysis you might conduct do not hold. In such cases, I would not normally recommend looking at reliability across, instead suggesting that you look at agreement within rating approach and then compare means and covariance (possibly even with a Pearson’s/phi approach) with those numbers. But this depends on your precise research questions and may need a theory-driven solution rather than a statistical one. I don’t know enough about repeated measures kappa to know if I should recommend it or not – I’ve actually never heard of it before now.
Dr. Landers,
Thank you for the response! Let me clarify a bit more: each of my participant were examined both by the gold standard and the standard I am testing. Would this piece of information change anything??
That is how I understood it, so no, it doesn’t change anything. 🙂
Dr. Landers,
Thanks for confirming! To be honest, I did not know about repeated measure kappa before I take over this project but I will definitely try the phi approach!
Dr. Landers,
My question is about an unconventional use for ICCs and any advice for working with multilevel (but not aggregation) data. We want to examine the agreement between two measures of sleep (both interval data). Participants complete a sleep diary of the number of hours slept, and wear an actigraph (a wristwatch-like device) that records their movement. Number of hours slept is computed from this movement. We are conceptualizing these as our “raters” of number of hours slept. First question: is this a reasonable extension of ICCs? Our research question is how well do these two measures (sleep diary and actigraph) agree on how many hours of sleep a person is getting?
The second question is a bit more complicated. Each participant completes the diaries and wears the actigraph for several nights. Am I correct in concluding that because we now have nested data (each “rater” has multiple ratings for each participant) we have violated the independence of ratings assumption and using ICCs for the entire dataset would be inappropriate? If so is there any correction for this or any way for ICCs to handle nested data? We don’t want to aggregate or use the data to answer any multilevel questions so I am struggling to find the appropriate analysis. We simply want to know how these two measures agree but we have nested data. Even if we cannot report an overall ICC for the entire dataset would it still be appropriate to report ICCs for each participant individually or would this violate the independence assumption since the measurements would be coming from the same person?
Any advice is appreciated. Thank you.
I wouldn’t recommend ICC in this case because you have meaningful pairings – rater 1 and rater 2 are not drawn from the same theoretical population of raters – instead they represent two distinct populations. Since you only have two you’re comparing, I would probably just use a Pearson’s correlation (to capture covariance) and also a paired-samples t (to explore mean differences). If you’re just throwing the means into another analysis, you don’t even need the mean differences.
You can calculate ICC for nested data, but you’ll need to do multilevel modeling. You probably should not do it in SPSS. I would recommend either R or the program HLM. You could instead determine ICC at each time point (not for each participant – that’s not very useful), but you do lose the ability to examine accuracy over time that way. You’d need, at a minimum, an argument that accuracy shouldn’t change over time for some literature-supported reason.
You might – maybe – be able to calculate ICC by hand using an RM-ANOVA, which could be done in SPSS, but I’ve never seen any work on that specifically.
Thank you for the reply. The reason we even thought about doing ICCs with this data is because other authors did but I wasn’t sure it was appropriate considering the multilevel nature of the data. Is there any way to do some type of modified Pearson correlation with multilevel data that you are aware of or would you recommend trying to run a multilevel model in R and getting ICCs from that?
I wanted to clarify since at first you suggested not running ICCs with this data but then once the multilevel issue come into play it seemed like you were suggesting it might be feasible.
To be clear, it’s feasible with appropriate justification (i.e., that you can argue the two approaches are drawn from the same population of estimators), so that has theoretical and interpretive implications which carry a certain degree of risk. I can’t tell you how risky that is without knowing the project or your research literature better. If prior researchers publishing in decent journals have done it the way you are doing it, it is probably pretty low risk.
I will say, however, that the disadvantage of using a single ICC versus a Pearson’s correlation (or even an ICC) at each time point individually is that if there are any subtle differences over time (e.g., if the actigraph becomes less accurate over time, or if diary entries are biased differently over time, etc), these could be washed out in ICC. If there are any large differences, it will just bias your overall ICC downward – that’s the risk of general summary statistics in data where there may be multiple effects. If you’re confident there aren’t any such effects, then it doesn’t really matter.
If you actually use a multilevel modeling program (e.g., HLM), you could alternatively calculate ICC given a three-level model – hours within measurement approach within time (or hours within time within measurement approach) – which might solve both problems.
Ok. Thank you for the help.It is appreciated.
Dear Dr Landers,
Sincere regards, would be great help if you pl help me with this.
i am measuring trust within software development teams by using scores on trust factors and scores are on scale of 0-5 i.e poor- excellent and i have 8 teams in total and will be same for entire exercise and also my items (trust factors) will also be same on which individual team members will give score(scores will be collected in 3 cycles after every 2 weeks after incorporating improvements in trust factors in which score is low) can you plz suggest which i should use ICC1 or ICC2 to measure inter rater reliability and which technique i should use for data validation
@sulabh
just to add little more information to my previous question as i will be taking scores from 8 teams and each team is having around 7-8 members(total 62 members approx) giving score from 0-5 scale on the trust factors and i have total 35 trsut factors on which i am seeking trust score . can you help me with which ICC1 or ICC2 i should procced and which technique will best suit for data validation?
many thanks
Sulabh
Since you’re aggregating, this is much more complicated than a statistical question alone. The type of ICC you need depends on the goals of your project. I would recommend you take a look at the aggregation article I’ve cited for others in earlier replies. Most critically, remember that ICC(1) and ICC(2) in the teams literature refer to ICC(2,1) and ICC(2,k) in the Shrout & Fleiss framework. You will probably need both, because they tell you different things.
Thanks so much Dr Landers,
can you plz suggest any article or provide me any link where i can study how to calculate ICC(2,1) and ICC(2,k) and also can i use exploratory factor analysis and Cronbach alpha for validating my data?
The Shrout & Fleiss article linked above discusses both version of ICC you are interested in (I believe as Case 2). An alternative conceptualizations is that presented by McGraw & Wong (1996), published in Psychological Methods, which uses the numbering system I’ve described here.
You could use EFA or CFA, but I would probably use CFA if I was going to take that approach. Cronbach’s alpha is the same as a consistency-type ICC(2,k).
Hi Richard,
Thank you for this informative post, it was very helpful!
I have a quick question about assessing the inter-rater reliability of a diagnostic measure (i.e., categorical data).
My sample will include 20 participants, with the same two raters assessing each participant. My variable is a dichotomous one (i.e., Yes/No based on whether or not the rater gave them a diagnosis using the measure).
So far, the two raters have assigned every subject the same rating, and therefore I am getting a warning when I run kappa on SPSS and it won’t provide me with a kappa statistic.
If my raters continue to do this, will I not get a Kappa statistic at all??
Also, other than Kappa, can you recommend another statistical measure to assess inter-rater reliability?
Thanks!
Remember that your goal is high reliability, not a high kappa specifically. Kappa is just an assessment of chance-corrected percentage agreement. In your case, I’d just use percentage agreement – 100% (reliability = 1).
Hi Richard, thank you for the clear explanations! Already used them several times to my advantage.
I have a particular question for which I don’t find an answer…
Students collected 64 voice samples that were rated for several (6) parameters on 2 occasions by the same group of 5 raters. Overall interrater would use the ICC (2,5) model, no probe there!
Remaining question: the students want to know which individual sample out of the 64 has the highest agreement/reliability on a certain parameter? they are trying to build a collection of ‘ideal’ voice samples for teaching purposes…
Should we calculate ICC between the 5 raters for a single sample and then choose the highest number? I don’t think this is the correct solution, but I’m stuck on this one…
Any ideas would be greatly appreciated!!
Thanks!
Jan
So, if this isn’t for publishing purposes, you have more options than you would otherwise. If you’re ok looking at agreement instead of consistency, I’d probably just calculate the standard deviation of ratings for each rater – the smallest SDs will have the least variance between raters. However, you should keep in mind that there will still be error associated with those SDs – don’t take them as a definitive ordering (this is why I mention publishing), but it should still get you what you need. If you wanted to look at consistency, you could probably modify this approach by converting ratings into z-scores and then calculating the standard deviation of the rating z-scores for each rater (this sort of lazily controls for rater mean differences).
Dear Mr. Landers,
thank you for all your explanations. But as you realized there are still some individual questions;)
So here is mine:
I have a huge dataset with several companies, employees and leaders. I want to analyze the self-other agreement in leadership. To assign the followers to their leaders I generated a new dataset aggregating the mean score of the self perceived leadership, the follower perceived leadership and the follower job satisfaction for each of the 300 companies. (Leadership was computed before out of 10 items of the questionnaire).
So my new dataset consists of 300 companies. For each company I have the three mean scores (self-perceived leadership, follower perceived leadership and follower job satisfaction). I want to run polynomial regression using self and follower perceived leadership as independet variables and follower job satisfaction as dependent variable.
In self-other agreement in leadership literature I read that you should compute an ICC score before you run the regression. So my question ist at what point and which ICC should I compute? Do I just have to compute an ICC between self and follower perceived leadership in my new dataset?
I hope my explanation of the problem is not to confusing.
Thank you in advance!
Best wishes
Jannis
I’m afraid I don’t know the leadership literature well enough to have an answer for you. My suspicion is that you’re conflating a few types of ICC – you need ICC to determine how well the individual follower ratings reflect the population individual and mean follower ratings before aggregation, and you’ll need some other type of reliability (although I wouldn’t personally go with ICC) to determine agreement between the mean follower rating and the leader rating. But that’s a bit of a guess. However, I’m confident that the articles on aggregation that I’ve posted in other answers (especially those related to rwg) will get you closer to what you need.
Thank you for your fast response!
I was thinking of the same, first computing ICC within the follower group. But how do I do that? I have about 19.000 followers. How do I compute the ICC within one group???
That’s interesting they were also reffering to the rwg in the literature. I have to look that up! Especially the article you cited: LeBreton, J. M. & Senter, J. L. (2008). Answers to 20 questions about interrater reliability and interrater agreement. Organizational Research Methods, 11, 815-822. Any clue if there is somewhere a free version of this article? I am a student in Germany and I don’t have free access to this article anywhere.
I am not blessed with that much money to pay 20 dollars for every article;)
Thank you again!
ICC isn’t calculated within one group – it is used to assess the consistency of all groups in predicting their respective leaders. If you have a variable number of followers per group, SPSS can’t do that – you’ll need to either calculate ICC by hand from ANOVA or use another program that can do it for you, like HLM.
I don’t know if that article is available for free.
Thank you so much for your help!
But I have one last question. So if I can only calculate ICCs between groups maybe I don’t need an ICC at all. Because for each company I compute the mean of all followers rating leadership in general. Additional I compute the mean of all leaders rating leadership in the company in general.
So that I have
Mean Rating Leadership (Leaders) Mean Rating Leadership (Followers)
Company A 4,3 3,9
Company B 4,1 2,8
Company C 4,9 4,5
Company D 3,8 1,9
….
….
Thanks in advance!
Jannis
The problem with ignoring reliability is that any reader/reviewer will not be able to tell how well your follower scores hang together. For example, on a 5-point scale, you might have 2 leaders both with a mean of 4.0. The first leader has scores ranging from 1 to 5 whereas the second has scores ranging from 3 to 4. That means scores of the second leader have greater reliability than those of the first, which is usually interpreted in the leadership literature to mean that the leader construct is more accurately assessed by people with leader 2 than leader 1. ICC is used to assess the degree to which this consistency exists on average across all leaders, across all companies.
At this point, I’d suggest you bring in a statistician onto your project; the more you write, the more it sounds like the aggregation strategy of your project is closely related to interpretation of your hypotheses, and if so, you would be better off with someone with expertise in this area (and preferably with leadership too) actually working on your project rather than just asking questions on the internet. 🙂
Dear Dr. Landers,
Our group of 3 raters each completed 5 rating scales for 20 patients at 3 visits per patient. The 5 ratings scale are diagnostic checklists, they are Likert-type format, each has different numbers of final categories/diagnoses, I treated them as ordinal. We are interested in “Absolute Agreement” between the 3 raters for all the visits and particularly at patient’s last visit. Using a ICC(3,1) – “Two-Way Mixed Model” with “Absolute Agreement”, our ratings for each scale range from .5 to .6 (single measures) and .7 to .8 (average measures) for all 60 visits.
When we looked at the ICCs for the last visit only (N=20), the ICCs are all lower for all 5 scales despite the ratings between the 3 raters are actually in more agreement at the last visit as the disease progressed. When I looked at raw ratings of one of the scale, there are only 4 cases (out of 20) of disagreement among the 3 rates (see below), but the ICC coefficient is .36 (single measure) in this case. The lack of variance among these raw ratings which should indicate “agreement” does not seems to be reflected in the ICC calculations? Did I do something wrong here?
Last Visit (N=20)
Rater1_Checklist 5 Rater2_Checklist 5 Rater3_Checklist 5
2 1 3
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 2
1 1 1
1 1 1
1 1 1
1 1 2
1 1 1
3 3 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
1 1 1
No, that sounds right. Your raters agree in 80% of cases (also a reliability estimate); however, in the cases where they disagree, the pattern is the opposite of predicted rater effects.
In this case, Rater 3 rates much higher than both Rater 1 and 2 in 75% (3) of cases where there is disagreement, but dramatically lower in 25% (1) of cases where there is disagreement – specifically, in the 3-3-1 case, in which case it is in completely the opposite direction. That harms reliability dramatically. If you change the 3-3-1 case to 3-3-3 (just as a test case), you’ll find that your single-rater reliability increases to .737.
The reason this has such an extreme effect is because you have so little variance. Remember that variance is necessary for ICC to give you reasonable estimates of reliability. You want variance, but you want that variance to be _predictable_. In your case, there just isn’t any variance in the first place, so the “bad” (unpredictable) variance is larger than the “good” (predictable) variance, driving your reliability estimate down.
This is the same principle at play in ANOVA (which ICC is based on) – you want there to be very small differences within groups but very big differences between group means to get a high F statistic. In this case, there are small differences everywhere, so your small inter-rater differences seem huge in comparison to your also-small inter-case differences.
Given your situation, I would probably just use percentage agreement, or even Fleiss’ kappa, as my estimate of interrater reliability with this dataset.
Thank you for the clear explanations! It makes perfect sense now. Percentage agreement would be easy to do for this dataset but it don’t think it takes into consideration agreement by chance? Thanks very much again for your insights, much appreciated!
It doesn’t. If you want to worry about that, I’d use Fleiss’ kappa.
I appreciate the simplicity that you use to explain a fairly complicated analytical method, so thank you! I wanted to clarify that I am using your technique correctly as I have a team of Patient Navigators who collected data from 900 community participants. The number of surveys were not equally collected across PN and I’m interested in the variance within each set of data collected by an individual PN as well as the variance between participants of different PNs. If I’m understanding your technique correctly, I would use the ICC (2) as I’m interested in the mean difference and would refer to the “average measures” in the ouput?
I don’t know the field-specific terms you’re using here, but if you’re saying that you expect the means across PNs to be equal, and if the PNs are each assessing the same group of participants, yes, ICC(2) would be the right approach, although I think you want to know ICC(2,1), single measures, to assess how accurate a single PN is in capturing their assigned group’s mean. If you have different participants by PN, you may want ICC(1). Remember also that you cannot assess ICC when your groups contain different numbers of cases using the built-in SPSS functions; you’ll need to either calculate it by hand or use another program designed for this (e.g., HLM).
I was wondering if you had any suggestion for entering in N/A from a global scale that goes from N/A (the target participant did not respond to the other participant because the other participant did not make any suggestions) to 5( the target participant responded to the other participants suggestions a lot). For reliability purposes only, I am wondering if I could enter a zero for N/A or if a value like 6 would be more appropriate.
First of all, there are no “reliability purposes only.” The way you calculate reliability must be matched to the way you actually use those scores – otherwise you have a meaningless estimate of measurement quality. So if you are not using scale scores of N/A in analyses, those cells are essentially missing data. If you do include N/A in your reliability estimate somehow, you must use those values in future calculations as you treated them for reliability (i.e., if you calculate reliability on scale scores with N/As represented as 0, any analyses you do must be on variables including that 0 too).
Whatever you do, you need interval or ratio measurement of the scale to use ICC. Since you are apparently already confident in the interval+ measurement of 1-5 (i.e., at a minimum, the distance between 1 and 2 is the same as the distance between 2 and 3, between 3 and 4, and between 4 and 5), you should consider if the same is true for N/A to 1. If so, you could reasonably recode N/A as 0. If not, you could instead consider the analysis of two difference variables, one binary-coded variable distinguishing N/A and not-N/A, and another with 1-5. But you will have missing data in the 1-5 variable that way, so be sure this is theoretically meaningful.
I was also wondering if you could clarify the difference between using single measures and average measures for your ICC variable. I understand that average measures is typically used in research, however I also know that you said that single measures is able to tell you how reliable a single rater is on their own. Is it okay to just use one of the ICC values or is it important to ensure that the ICC values is above .07 for both the single and average measures?
Thank you
It’s only typically used in research because that is what researchers are most often (although not always) interested in. Remember that reliability is conceptually the proportion of true variance to total variance – so a reliability of 0.7 means that 70% of the differences between scores can be attributed to something stable whereas 30% is something that isn’t. In ICC’s case, the 30% is attributed to differences between raters.
If you only have one rater, the rater-contributed variance is much higher because you don’t have many different raters to average across. All of the mismeasurement caused by that rater is present, and your numbers will be randomly weird. When you have two raters, it’s essentially cut in half – Rater 1 is randomly weird and Rater 2 is randomly weird, but because you’re taking an average, a lot of that random weirdness averages out to zero.
So it depends on what you’re trying to do with your numbers. If eventually a solitary person will be making these judgments (or you’ll be using a single instrument, etc), what you want to know is how much of the variance that rater is capturing is “real”. That’s single measures. If you will always have multiple raters and will be taking an average, that’s average measures. If you’ll be using a different number of raters than you actually had available for your reliability study, you can mathematically derive that reliability from either of the two you already have.
We have created a composite score of two of our variables and I was wondering if in that case you would use the ICC from the average measure because we added together scores on the rating scale from the two variables OR if we would still look at the single measures because each of the coders will eventually be going on their own to code the videos.
Thanks you
Average measure refers to the raters, not the scale the raters used. You want single measures if you want to know how well a person can code a video on their own.
Dear Dr. Landers, I would like to test inter rater reliability of a patient monitoring tool. Both investigators have been asked to monitor 10 patients and identify care issues. I have assigned a score (out of 1) to each rater by seeing how many care issues each identified out of the total care issues identified by both i.e. if 5 issues have been identified 4 of which are common for both and 1 rater identified 4/5 I assigned a score of 0.8 whereas the other rater identified 5/5 therefore I assigned a score of 1. Which test would be most suitable in this case to test for reliability please?
It depends if you have access to the original data or not. It also depends on how many total issues there are. If you have the original data, and hopefully you do, you would probably want to code the agreement across each dimension, preferably coding 0 for absent issue and 1 for present issue, then use a kappa (or even percentage agreement) to assess each agreement on each issue individually.
However, for all of this, 10 cases is going to produce a massive confidence interval – the reliabilities you find will be highly volatile.
You probably do not want to use ICC on your percentages unless your goal is to assess “in general, how much do the investigators agree”, in which case you’d probably just want to report the mean of those proportions (i.e., mean percentage agreement), but that would camouflage any by-issue disagreement, which may or may not matter to you. You also might be able to justify ICC(2,1) depending upon your hypotheses, but I don’t think ICC(2,k) would be interpretable unless you’re going to use the mean agreement percentage in some sort of follow-up analysis.
Hi Dr Landers,
I am confused how to set my data up. I am looking for rater reliability of a tool to measure healthcare worker competence in evacuation. We have designed a rubric (face/content validity established). The rubric is divided into multiple tasks that are complete, partially complete, not complete (2,1,0). There are also several points where time is measured to complete the task. We recorded the evacuation of 3 patients in 3 different scenarios (Poor, Average, Good). We showed the video to a group of 10 raters. I know that I will have 10 raters for the columns (Hopefully that is right). Do I then put each of the ratings for the 3 groups of videos as rows for the individual items?
What do I do with the time measurements of the task?
Wish I was a statistician…..
From what you’ve described, it doesn’t sound like you have enough cases for an assessment of reliability – it doesn’t sound like you have replication within each condition, which you need. It also sounds like you have multiple measures being taken within each video, possibly, which would violate independence assumptions of any reliability assessment, but it depends on your research goals and influences what sorts of conclusions you can validly draw. I think you’re going to need to bring in someone in a fuller capacity than I can provide via blog replies. 🙂
Thanks for the response. Would you please remove my last name from the post or remove the post? I didn’t realize I could post without my full name. Thanks
Dear Dr. Landers,
Thanks for your prompt reply! I do have access to the original data. In these 10 patients I have identified a total of 29 care issues.
When you told me to code agreement across each dimension .. in this case dimension refers to each patient or to each observer?
In this case 1 observer detected 22 issues (in 10 patients) and the other 23 issues (in same 10 patients) however these were not always common for both in fact the total number of issues was 29.
The hypothesis is that the tool is reliable enough for patient monitoring… no follow up analysis as such will be carried out.
Thanks and Regards,
Maria
Dimension refers to each issue. If you have 29 issues that are distinct, you have 29 possible scales on which to agree, which means you need 29 estimates of reliability.
Alternatively, if you are saying all 29 issues are unidimensional (i.e., all measure the same underlying construct), then you should convert all of them into binary indicators (1 for present, 0 for absent), calculate the mean score for each rater, and then assess the reliability of those mean scores.
Hello Dr. Landers,
Thank you for your posting on this topic! I was hoping you can verify that my current calculations on SPSS are correct? For my study, the same two individuals assessed 15 patients each with the same 25 questions. The 25 questions can be grouped into 5 questions each based on concept. The columns are labelled Person 1 and Person 2, while the rows are the 15 patients. Each cell is the mean score of 5 questions in a concept. Since there are 5 concepts each with 5 questions, then there are 5 data sheets. I determined the two-way mixed methods ICC value and Chronbach’s alpha value for the mean scores of each concept. Is that correct?
Thank you for your input!
Maya
Unless you’re interested in conducting scale diagnostics, you don’t really need alpha in this context, since you are already getting an estimate of reliability of the means from ICC. You will probably end up with 5 ICCs – one for each concept – unless you have reason to believe the concepts are unidimensional, in which case you would probably just want 1 ICC. Otherwise this sounds pretty normal to me.
I was also wondering how to go about determining an overall cronbach’s alpha value and ICC value?
Hi Dr. Landers,
Thank you for being here. Wishing you always in good health and prosper…so we could always haveyour guide and expertise.
Dr. I have a few questions. It may have been addressed here but since Im using my cell, checking your previous comments is a bit limited. My queries:
1. If I need to check the percentage of raters between two known raters on a test question, what is the least number of students required to be able to be executed in the SPSS? If the number of students is less than 5, can these still be calculated in spss?
2. In another case, there are two known raters, for 10 question test. Will 20 students suffice to determine the percentage of raters?
Looking forward to your help.
Best regards
Aimy
To calculate an ICC, you just need inter-case and inter-rater variance, so I suppose the minimum is 2. But your confidence interval (i.e., the mismeasurement of that ICC) is going to be pretty high with so few cases.
It’s not really possible to give a specific number of students without knowing what the ICC is ahead of time – what you’re asking about is essentially a power calculation. So the greater agreement you have, the fewer cases you need to detect it.
Dr. Landers,
Thanks very much for this useful information. Two questions: 1) Could you verify that I’ve made the correct choices for decisions 1, 2 and 3? 2) Do you have a citation for the recommendation you posted about using scale means and not individual items (see below)? This makes sense to me and a reference for the paper where we’re doing exactly this would be great.
“A special note for those of you using surveys: if you’re interested in the inter-rater reliability of a scale mean, compute ICC on that scale mean – not the individual items. For example, if you have a 10-item unidimensional scale, calculate the scale mean for each of your rater/target combinations first (i.e. one mean score per rater per ratee), and then use that scale mean as the target of your computation of ICC. Don’t worry about the inter-rater reliability of the individual items unless you are doing so as part of a scale development process, i.e. you are assessing scale reliability in a pilot sample in order to cut some items from your final scale, which you will later cross-validate in a second sample.”
Study Design/Research Question: We have 126 mothers and 126 fathers who each separately rated their assessment of the father’s involvement with their child(ren). Each set of parents rated one or more children on 8 dimensions of father involvement (mean scale scores based on some set of individual continuous items). Our research question focuses on the extent to which the parents agree on their assessment of father involvement for each child (not across children in cases where they report on more than one child). We want to report the ICC’s associated with the various ratings.
Decision 1: one-way random effects or ICC(1)
Decision 2: individual (not average)
Decision 3: absolute agreement (not consistency)
Thank you so much in advance for your time.
PCharles
Since you have meaningful pairs (always one mother and one father), I would probably use a Pearson’s correlation in this context. Using ICC means you that you are assuming that mothers and fathers are drawn from the same population of judges about the father’s involvement (i.e., mothers and fathers are drawn from the same population of people with opinions about the father’s involvement). If you expect mothers and fathers to have different perspectives on this, you probably don’t want ICC. But if your goal here is to get the most accurate rating possible of father involvement for later analyses, you could use ICC(2,k) to assess the mean of their two ratings, with mothers and fathers as consistent raters (i.e., mother as rater 1 and father as rater 2).
I don’t have a reference handy for that idea.
Dear Dr. Landers,
I have read through all the responses and still could not find an answer to my question. I have conducted an online questionnaire and asked multiple choice comprehension questions for a case study.
I have 5 comprehension questions and answers are multiple choice (coded as 1-0). There are 85 respondents. My mentor asked me to provide intra-corelation of the comprehension questions.
– I have located the answers from each respondent on the columns (86 columns) and 5 questions on the rows and run ICC (two way mixed). Is this a correct approach to find the intra-correlation of the questions for the reliability?
Many thanks for supporting us!
Kind Regards,
I assume by “intra-correlation” you mean “intraclass correlation.” These are slightly different concepts though.
First, this is an atypical use of ICC. In most cases like this, you would calculate coefficient alpha – although, in this case, alpha is actually a special case called a KR-20, since you are working with binary data.
Second, if you wanted ICC anyway, your rows and columns are reversed, and you probably want two-way random.
Thank you very much Richard.
It’s so well-explained! I have used it for my master’s thesis. You’re great!
But, now, I would like to citate this source in my project. Could you provide me with the citation of this (article?) ?
Thank you loads!
Gemma.
There is not really any “easy” citation for this page right now. You could cite it as a webpage, I suppose. I will have a DOI and source for it in the next couple of months though and will add a reply then with more info.
Dear Dr. Landers,
many thanks for your comments. I used KR-20 as you have suggested. Kind Regards,
Dear Dr. Landers,
Thank you very much for your contribution!
I am currently conducting a study and I have some problems on the statistical analysis. I am not sure if my problem can be addressed by ICC. Hopefully you can give me some insight.
I have interviewed 3 members (father, mother and child) of a family. All of them answered a 5-item questionnaire, in a 5-point likert scale, which tested on the level of permissiveness of mother. I would like to know how the patterns of their answers related with each other.
I would like to know if it is still correct if I do my data set like this:
………….father……mother……child
item 1……2…………..3……………3
item 2……1…………..2……………1
item 3……2…………..2……………1
item 4……1…………..1…………….1
item 5……2…………..1…………….2
I suspect that it twists the usage of ICC and I do not know if it is still statically make sense.
Thank you very much for your help!!
ICC is going to assume that your three raters are all drawn from the same population. Thus, using ICC means that you expect the father, child, and mother to provide the same sort of information. If you don’t think that’s true – and it doesn’t sound like you do – then you shouldn’t do that. I would instead just use something like ANOVA and calculate an effect size. Eta-squared would tell you the proportion of variance in your ratings explained by their source, so I’d probably recommend that.
Dear Dr. Landers,
Thank you for your prompt and clear explanation!
I am glad that you suggested me an alternative way so that I know the direction to work on!
Millions of thanks!
Dear Dr. Landers,
Thank you for your prompt and clear explanation!
I am glad that you suggested me an alternative way so that I know the direction to work on!
Millions of thanks!
By popular demand, this article has now been published in the Winnower for your citation needs. You can cite it in APA as:
Landers, R.N. (2015). Computing intraclass correlations (ICC) as estimates of interrater reliability in SPSS. The Winnower 2:e143518.81744. DOI: 10.15200/winn.143518.81744
You can also download it as a PDF here: https://winnower-production.s3.amazonaws.com/papers/1113/v12/pdf/1113-computing-intraclass-correlations-icc-as-estimates-of-interrater-reliability-in-spss.pdf
Hi Dr Landers,
Thanks very much for the very informative article. I do have some follow on questions, however. I am doing a study attempting to assess inter-rater agreeability/reliability. 3 raters (doctors) were tasked to rate a group of 48 identical ratees (patients) each for 6 variables (A-F) on a 5 point linkert scale measuring stability or progression of different risk factors in a disease. My first question is regarding the type of ICC test chosen in SPSS. Would it make sense in this case that a 2 way mixed type ICC should be chosen due to the fact that raters in this situation are specific to their own experiences as doctors? Or could their ratings and subsequent measure of agreeability be generalized for the population thus making the case for a 2 way random type ICC to be chosen?
Secondly, I’ve been exploring the different kinds of statistical tools available for analyzing inter-rater reliability and was wondering, between the ICC and the relatively new fangled Krippendorf’s alpha – would you recommend one over the other when it comes to assessing ordinal levels of data which potentially should be weighted?
Thanks very much for your time and effort for all the help you’ve put into this post.
Best regards!
It depends on to whom you are trying to generalize. If you want to run statistics generalizing only to those three doctors, 2-way mixed. If you want to run statistics generalizing to doctors, in general, 2-way random.
I believe ICC is a specific case of Krippendorf’s alpha – I believe they will be identical under the conditions both could be calculated. However, ICC can’t be calculated on ordinal data (it relies on meaningful rater means), so I suppose I’d go with alpha in your scenario.
Dear Dr. Landers,
I hope this question has not been asked before. I apologize if I missed it going through the previous posts.
I have the following study design. To examine the reliability to of two different methods to assess gait (one based on a human analysis, the other based on a computer) we asked 3 raters (human analysis) to rate gait and had two identical computers. 20 participants walked 6m at their usual speed three times and the three humans and two computers had to assess their gait speed.
This means that each rater measured 20 participants 3 times (trial 1, 2 and 3). I want to compare the ICC for the human raters with the ICC of the computers. I can calculate the ICC for the three human raters for each trial (1, 2, 3) and the two computers for each trial (1, 2, 3) but then have three separate ICC values for the humans and 3 separate values for the computers.
Is there a statistical way to combine the 3 trials so I will only have one ICC for the humans and one ICC for the computers?
Thank you for your advice,
Bjoern
Maybe. ICC assumes that all cases are drawn from a single population of raters, and a single population of cases. If you have multiple trials, you have a new source of variance: time. If you think that the differences over time potentially create meaningfully new outcomes, you’d want to look at reliability separately for each time point, or model it explicitly somehow. If your three time points are themselves just a sample of a single population of assessments, and you just want to know mean reliability, you can do so – since ICC is a reliability estimate, it’s a percentage, which means you can just calculate a mean. The only problem with doing so is that there’s no established way to calculate a confidence interval around a mean ICC that I know of. So if you want to compare the mean human ICC and mean computer ICC, you’d need to do so based upon the absolute difference between those ICCs alone, versus any sort of hypothesis testing. I don’t know if that meets your needs or not, but that’s the best I can think of.
Professor, I am graduate student studying in Korea.
I found your webside by chance while searching for statistical method. Thankfully I could learn a lot. I really appreciate you!
Currently, I am doing a research on organizational culture, and planning to aggregate individual responses on organizational culture data to organizational level construct.
Your guidance is very helpful for me, but I wonder whether my data is appropriate.
I measured organizational culture without using likert-type scale.
Respondents distributed 100 points across each of the four descriptive statements of organizational culture depending on how well they matched their company. (this way of classifying culture is called competing values framework – hierarchy, market, clan, and innovative culture)
Therefore, the total score distributed across each of the four culture totalled 100, and each person rates each culture such as 25, 50, 15, 10. I would like to create overall organizational culture scores for each company by averaging (aggregating individual responses). One company, for example, will have 30, 15, 20, 35 scores of each culture type.
As I heard that usually the guidance is appropriate for likert-type data, I would like to ask you that
1) whether this type of data is appropriate for your guidance as well.
2) If not, could you please recommend the way how I can justify the use of aggregated individual level scores as higher level data?
3) Someone recommended me to change the responses to liker-type scales (0~20 -> 1, 20~40 -> 2, etc.) Then, is it possible to follow your guidance?
I appreciate your time for consideration on my questions in advance.
Have a great weekend.
Jeongwon Lee,
You’ve actually combined several different problems into one project, so I don’t have a good answer for you, although I can give you some guidance on the hurdles you need to clear.
Problem 1: Distributing scores among 100 points means you have ordinal data, meaning ICC (and alpha, and rwg, and all the other usual stats used here) cannot be used.
Problem 2: The ordinal data you do have are ipsative, meaning scores cannot be compared across people, since people can assign whatever ranks they want among the four statements. For example, when comparing a person that ranks 90, 10, 5, 5 versus 60, 30, 5, 5, you have no way to know if the first person judged culture on the first dimensions dissimilarly from the second. If you’d asked them on a Likert scale, both the 90 and 60 could correspond to “Strongly Agree.”
Problem 3: You need to justify aggregation, not just assess reliability, which is a more complicated process. You need to establish two things: one, that each person’s view of culture maps onto the team’s view of culture to an acceptable degree (the level varies by whom you ask), and two, that the consistency of that view across people is sufficient to get a stable estimate of company culture.
In the presence of Problems 1 and 2, I am unfamiliar with any approach that will solve Problem 3. However, those are the three issues you will need to work through. It will probably involve multi-level structural equation modeling and estimators that can be used with ordinal scales. Good luck!
Dear Dr. Landers,
I really appreciate your comments!
I could figure out problems that my data have. Although it seems not easy to solve, I will try to solve those problems that you help to give me some guidance on.
I would like to thank you again for your kind help.
Jeongwon Lee
Dear Dr. Landers,
Thank you a lot for this post, I found it extremely well-written and useful!
I am dealing now with ICC and I have an issue in my analyses.
I have an experiment with 12 annotators coding a time value (the time of a scpeific occurrence) for 40 events. In some cases, I do have missing values (the annotator might not have coded the event or might have forgotten to save his answer). If I run the ICC in SPSS, the events with missing values are eliminated from the test. Is there any way to replace those missing values?
If I replace the missing values with”0″ or any other continuous value, the analyses are not correct anymore.
I also thought about running 2 analyses:
1) Fleiss kappa with a dataset that contains only categorical variables (“0” for missing values and “1” for annotated values) to check the inter-rater reliability for the missing values.
2) running the ICC on the events that do not have missing values and compute the corresponding coefficient only for those events.
I would really appreciate your help on the topic.
Thanks,
Giulio
There are many approaches to missing values analysis. The easiest option is mean replacement, where you enter the mean of the other raters for your missing value. However, there are many limitations/assumptions to that approach. I would suggest you use the Missing Values Analysis procedure in SPSS and select the EM algorithm for imputation. Also set the option to “save new dataset” (I believe in an Options or Save menu?) – then run your reliability statistics (and all analyses) off of the dataset it imputes.
The key to making that decision though is what you are going to do with missing values later. If you’re going to use listwise deletion when there aren’t 12 raters (not generally recommended), then you’ll want to use listwise deletion before you calculate reliability, and then you don’t want to do any imputation. If you’re going to use imputed values for reliability, you need to use them for analyses too. Everything needs to match.
If you do want to do missingness imputation, there are procedures to determine if your data are essentially “missing at random” (MAR) (vs. not missing not at random; MNAR). Your data must be MAR (or essentially MAR) to justify this sort of analysis in the first place. I don’t have any papers handy, but my recollection is that as long as less than 10% of your data are missing, you are safe assuming MAR and running missing values imputation. But you might want to look into the research lit on that.
Dear Dr. Landers,
I’ve previously written to you to ask you about the use of one-way ICC to derive the intraclass correlations of twins. Can I confirm with you whether the data need to be normally distributed? Also, should I be looking at the ‘single measures’ or the ‘average measures’ row to get the ICC in my case?
Thanks and best regards,
Yi Ting
Yes – ICC is based upon ANOVA, so all of the same assumptions apply – independence of observations (by pair), normality both between and across groups, etc.
For the sake of example, let’s imagine that you’re having twin pairs rate their satisfaction with their parents. A single-measures ICC will tell you the extent to which a single twin’s opinion speaks to population twin satisfaction with parents. An average-measures ICC will tell you the extent to which the mean opinion within each set of twins speaks to population twin satisfaction with parents.
Dear Dr. Landers,
Thank you very much for your detailed answer.
I will follow your suggestions.
I do appreciate your help,
Giulio
Thank you Richard for this explaination. I am just confusing if I can use ICC in my situation or not. I am working on my dissertation for master. It is about sentiment analysis on texts. I have 428 different texts. I applied a code for sentiment analysis and I retrieved results from -1 to 1. Then, I used the code with same text but translated to other language and I found a different results. I also have different result from 3 inter-rater. I just want to figure out how these sets are agreed or not. Is there a significant different between them? and If there I will look to data in more detail.
Thanks,
It sounds like you have three numbers to compare – the mean of 3 raters, the result of sentiment analysis, and then the result of sentiment analysis on translated data. If that’s correct, you can use certainly use ICC to determine the reliability of your rater mean, assuming that your ratings otherwise meet the assumptions of ICC. To compare the rater mean and two sentiment analysis results, assuming they are all on the same scale, you might want to use an ANOVA.
Thanks for replying,
sorry for that but why do you assume that I will compare with the mean of 3 raters. I thought it must be compared each as a seperate classifier. For that, I was assuming I have 5 rows of comparing. One is the result of sentiment analysis in the origin text, the second is tesult in translated version and the last three are the 3 raters. Is calculating the mean is an efficient way?
Another thing, I did not think of ANOVA because of the assumptions related to ANOVA that my not satisfied on my data sets.
Thanks.
The analysis should be driven by your research question. I was assuming that you’re interested in to what degree your raters and the two unique sentiment approaches differ from each other. If that’s not true, for example if the raters are not drawn from a single theoretical population of raters, you should not test it that way.
If your data don’t meet the assumptions of regular ANOVA due to non-normality or the use of rank data, then you might use a Kruskal-Wallis ANOVA, which is non-parametric. But you said your scores varied from -1 to +1, which sounds like ratio-level data, on the surface of it. If you have hierarchical nesting causing non-independence, then things get more complicated.
Thanks Richard for replying. Yes, your assumption is correct. I am interested in to what degree raters and the two sentiment approaches are agreed or disagrees. And which version is more similar to human judgement. So, Do you think it is better to calculate the mean? Because I was thinking to compare the two sentiment approaches together with raters.
I tested ANOVA before with two approaches and each rater individuallyt. However, the result always meaningless. For that, I assumed a violation in the ANOVA assumptions. In addition, I am interisting to show how much they are agree or disagree, not just if there is a difference or not.
Thank you so much.
You really need to think carefully about what populations you are trying to compare here, because that should drive your analysis. To the extent that you have multiple measurements of a given population, you should assess reliability for those measurements, and then compare the resulting groups. If you want to compare group means, you should take an approach that does that, such as ANOVA (or, if failing normality assumptions, a Kruskal-Wallis ANOVA). If you want to compare ordering, you should take an approach that does that, such as regression (or, if failing normality assumptions, something that compares rank orderings, such a Spearman’s rho or nonparametric regression). All approaches assume you have the same scales across all of your population measurements, which in your case I believe means all scores should be meaningfully anchored between -1 and +1. You also can’t mix and match assumptions – your raters and techniques must all be on the same scale, with the same variance.
I don’t know what you mean by “assumed a violation.” Most violations are themselves testable. You need to figure out what shape your data are and then choose tests appropriate to those data and the assumptions that can or cannot be made. Then you run tests. Finding a result you didn’t expect and then changing your approach solely because you didn’t find what you wanted is not valid.
I’m doing a book evaluation research using Bloom’s taxonomy with 4 analysts including me as the researcher. I use the taxonomy (Cognitive level 1 until 6) for every question We find in the book & categorize it into C1, 2,3,4,5 or 6. After all the analysts finished, then I want to check if there is inter-rater reliability (if all the analysts categorizing all the questions reliably). What formula should I use to check this. Thank you.
I don’t know. You need to determine its scale of measurement first.
HOW CAN I INPUT COMBINE VARIANCES INTO AN ERROR TERM WITH CONSTANT VARIANCE TO REPLACE THE CONSTANT VARIANCE.
Dear Dr. Landers,
Thanks for your informative article I’m hoping you can confirm I’m on the right track. In my study I have 60 subject dogs. Both the dog’s owner and the dog’s walker each filled out an established personality instrument that rated the dog on 5 dimensions. I’m interested in the inter-rater reliability of the dog walker and owner assessments. I’ve established that that ICC(1) is appropriate because each rater only rates one target, however I’m not sure about the average measure vs single measure. The instrument is a k-item list so scores from the raters are an average so I believe average is correct but I’d like to confirm.
Thanks again.
It depends on why you want to know. If your goal is to compare assessments between the two sources, you shouldn’t be using ICC – I would use a Pearson’s r. If your goal is to interpret the means across the two sources or to use those means in other analyses, you want average measures: ICC(1,k).
Thank-you so much for your response. I will be doing both Pearson’s r and ICC to analyze the data. I’ve been using this paper as a framework, which suggests doing both of those analyses.
Stolarova, M., Wolf, C., Rinker, T., & Brielmann, A. (2014). How to assess and compare inter-rater reliability, agreement and correlation of ratings: an exemplary analysis of mother-father and parent-teacher expressive vocabulary rating pairs. Frontiers in psychology.
I am doing an interrater reliability study of the rubrics used for grading by instructors at the American College of education. I set up 5 “mini-studies.” For each mini-study, 4 instructors are grading the assignment papers of 12 students. Two papers are graded for each of the 12. The rubric has six criteria and a total score, so I am examining reliability for the six criteria scores and the total score. For each criterion, scores from 1 to 5 are issued. In students’ regular classes, they will be graded by one instructor. Therefore, I think I am correct in using the ICC single measures coefficients as my reliability indicators. I’m interested in agreement but also whether or not students are being ranked the same across judges. So I’m running the ICCs for absolute agreement and consistency. The SPSS outputs also give me pairwise correlations among the graders and a mean correlation. I’m not sure if any of the other numbers I can get in the outputs are useful for interpretation. — In addition to the ICCs, I’m computing by hand possible agreement versus actual. The maximum pairwise agreement among the four professors is six. I’m defining agreement as exact, within 1 point, within 2 points, and within 3 points for the total scores which are each 30 or less. I could share more detail but would just appreciate knowing if I’m correct in what I’m doing and if there is anything I should be doing that I’m not so far. Thank you for your help.
Single measures sounds right for your purposes, and the differences between consistency and agreement sounds theoretically interesting for you, so you’re all good there. If all you want to know about is reliability, the ICCs are the only numbers you need. Pairwise correlations among graders can be useful if you’re trying to determine why the ICCs are low, e.g., general disagreement or disagreement caused by one particular person.
While you certainly can calculate the extra agreement numbers the way you are describing, that information is contained within the ICC and is not really necessary. If you want to know if a particular rater is causing a problem, there are better ways to do that (such as the pairwise correlations, or also an ANOVA). But I can see why you might do something like that if you’re going to try to translate what you did for a non-statistician audience.
One more quick question if you don’t mind. Can I average the single measures coefficients across the five mini-studies, and do I need to do a Fisher’s z transformation to do so? Thank you again.
An ICC is a reliability estimate, so it is a proportion – essentially on a scale from 0 to 100% – so you can just calculate an average of ICCs, if you need to know mean reliability for some reason.
Dear Dr Landers,
Thanks for your very informative article. Can you please confirm I’m on the right track? In my PhD study I have a total of 251 essays, which are rated by a single rater (myself), but a subsample of them (10) are double-rated by myself. How should I proceed to calculate intra-rater reliability? Which ICC is the most suitable for my case? Should I consider only the 10 essays which are double-rated or the whole sample of essays? I assume that the more essays I double check, the better, amb I right?
I hope you can answer my doubts.
Thank you very much in advance.
That’s an unusual situation for ICC since you can’t really be considered a random sample of yourself, which is required of ICC. I suppose you could use ICC(1,1), if you were to assume that you are a totally unbiased source of grading, but there are still some other assumption violations involved. Specifically, you can’t really assume upon second grading that you were unaffected by the first time you graded them, which is a violation of the independence assumption. You really need a second grader using the same criteria you are using. If you don’t have that, I would probably use a Pearson’s correlation instead, since you have meaningful time 1 – time 2 pairs. But that’s not precisely a reliability estimate for your situation.
You can only calculate reliability if you have replication, so it is only calculable on the 10. Just like with study design, the more cases you have two ratings of, the more stable your estimate of ICC will be (i.e., a smaller confidence interval). N=10 is not going to be very stable; if you want to calculate reliability on a subset, I’d personally want at least 25% of my final set.
Thank you for clearing things up and for the opportunity to ask questions, Mr. Landers.
I have a question of my own and I would gladly appreciate if you can answer my question.
My research group developed an instrument that can test the knowledge of students of a certain physics topic. After the development, we asked three experts (i.e. physics professors of our university) to rate the developed instrument using a validation rubric. The validation rubric is a questionnaire where criteria are listed and the expert will rate whether the listed criteria is evident in the developed instrument or not through a Likert scale where 5 means that the criterion is highly evident in the instrument while 1 means that the criterion is not evident in the instrument.
The rubric listed six major groups of criteria which are Objectives, Content, Illustrations, Diagrams and Figures, Language, Usefulness, and Scoring/Assessment Method. The following link shows a chunk of the data that we have gathered [http://imgur.com/wK4RKJI].
Since the data is a Likert scale, do you think it is appropriate for us to use ICC for the reliability of their ratings? If yes, what model should we use? Also, should we get the ICC for each major group (e.g. one ICC for Objectives, one ICC for Content, etc.) or should we get one ICC for all? If we should get one ICC for each major group, then how can we determine the overall ICC?
Thank you very much, Mr. Landers. Again, your response will be a great help for our study.
1. That varies by field. If your field is comfortable calculating means on Likert-type scales, then yes. If they usually use non-parametric tests, then no.
2. If all 3 experts rated every case, probably either ICC(2,1) or ICC(2,k), depending upon your goals. The article above explains this decision.
3. One for each variable you’re going to use somewhere else or interpret.
As the individual is attempting to validate the content of the instrument would this not be better handled using a content validity index? I dont think you are looking for reliability of the ratings you are looking for an overall rating of the validity of the tool?
I wouldn’t recommend that except in very limited circumstances. The CVI is a bit unusual. For the most part, it has only been commonly adopted in nursing research and a little bit in medicine more broadly, although it’s been introduced more broadly than that (including in my own field, industrial psychology). In most fields in the present day, content validity evidence is created through a process in which subject matter experts are consulted at multiple points, including to approve the final scale. In this context, the CVI is not really necessary except as a type of cross-validation (e.g., with different experts). In the OP’s case, even if such a statistic would be relevant, it would likely require a new data collection effort, and I don’t think it would provide much better evidence that what was already described… but it might still be worth looking into, assuming that the OP did not also need to introduce the CVI to their field (which is likely, outside of medicine).
Dear Dr Landers, thanks for providing this very helpful page. Could you please give an example for a case in which the raters are the population (and not just a sample)? Thank you a lot in advance!
Imagine you were running a triage unit at a hospital. Everyone that comes in needs to be triaged, but you’re worried that your triage nurse team (12 people) have different priorities when determining whom needs care first. In essence, you want to know how reliable a single nurse is in making that judgment. So to assess this, you ask for pairs of nurses to provide judgments on each person that comes in. Since you’re only interested in the reliability of the 12 nurses you have now, you want ICC(3). Since you want to know how reliable one of those 5 nurses is when making judgments alone, you want ICC(3,1).
If you wanted to be able to generalize from the 12 nurses you have now to any nurse you might ever hire, you would calculate ICC(2,1), but you’d need to assume that your hiring process for future nurses would be the same as past nurses (i.e., ICC(2) requires an additional assumption beyond ICC(3), which is why reliabilities are usually a little lower with ICC(2)).
Another example: we’re a party of 6 ENT-surgeons aiming to validate a specific protocol on scoring endoscopic video recordings of people swallowing different foodstuffs. Since there are >50 patients to score (each patient takes about 20 min to score), we were interested to see how well any individual of our ‘peer’ group faired compared to the remains judges, in order to allow a single judge to score several exams without being controlled by others… (so the judges were the population since nobody else would score the exams)sadly, results were really bad, but thanks to Dr. Landers we found out! Question remains: how to interpret the single results (1 judge) versus the ‘population’… what constitutes a significant difference to not allow the single judge from scoring future exams…
Yeah, identifying particular raters that are “problems” is a question without a clear answer. You just have to decide how different is different enough, in terms of means, covariances, or both. You might even try an EFA – I think that would be most interesting, personally.
Dear Dr. Landers,
I am supervising a number of Assistant Psychologists responsible for assessing patients taking part in an RCT examining the efficacy of cognitive remediation therapy for schizophrenia. Two of the outcome measures require the APs to make clinical judgements about the severity of patients’ symptoms. The PANSS contains 30 items each rated on a 1-7 scale, and the CAINS has 13 items each rated on a 0-4 scale. I have trained the APs to use these tools and we have randomly selected approx 10% of patients from the RCT to assess our interrater reliability (IRR) on the PANSS and CAINS. For each case selected for IRR there have been two raters (myself and another AP). The purpose is to assess our reliability as raters.
Your advice is much appreciated.
Thanks
Dr. Danny O’Sullivan
Your design implies to me that you are interested in the consistency of ratings between you and the assistant psychologists. In that case, I would probably use a Pearson’s correlation, since you are consistently one case and the AP is consistently the other. If you want to assess the reliability of the scale in general, you appear to be violating the assumptions of all types of ICC; you should really be randomly choosing a pair of ratings from all available raters for ever rating task. Or counterbalancing would work too. But having 1 rater consistent and the other rater inconsistent makes it impossible to parcel out the rater-contributed sources of variance, i.e., there’s no way to find out if your ratings are biased, which is a problem because you are 50% of every rating pair.
Having said that, you could still theoretically use ICC(1), but only if you _assume_ yourself to be equally as skilled as the APs. That may be a risky assumption.
Thank you so much for this very helpful article. I just finished a study comparing two methods of diagnosis for autism: a new procedure v. a gold-standard procedure. Both result in a 1 (= autism), or 0 (=not autism). I am comparing the dichotomy across methods (new v. old, 1 rater each) and across two raters (new, rater 1 and rater 2). I see that ICC is not appropriate for dichotomous variables, but is kappa the appropriate statistic for this analyses? I hear conflicting information. Thank you for your help!
Yes, ICC won’t work. Kappa is fine, although conservative. I usually report both proportion agreement and kappa in such cases.
I am doing a patient study that looks at the ICC of 2 observers (stays the same). In my study we make these 2 radiologist look at the MRI images of the same 30 patients.
In this study, since there are no repeat measurements, can we only use the single measurement. Or is there a place available for the average measurement?
I’m not quite sure what you mean. If you have both radiologists rating all 30 patients, you can calculate ICC. If you have each radiologist rating half of the patients, you can’t. I would recommend you follow the steps described above to figure out what kind.
I’m not quite sure what you mean. If you have both radiologists rating all 30 patients, you can calculate ICC. If you have each radiologist rating half of the patients, you can’t. I would recommend you follow the steps described above to figure out what kind.
Hey mike, thanks for the speedy response. I have 2 radiologists (don’t change), they each look at all 30 patients independently. None of them looks at the same patient twice, so all radiological imaging assesment takes place once. I know I will be using a two way mixed effect model.
I am just not sure if I can also use the average & single ICC. Since all the assesments were done once, can I even use the average ICC score?
I don’t think you understand the difference between average and single measures. The question you need to ask is if you want to know the reliability of a radiologist’s opinion (single) or if you want to know the reliability of the average of two radiologists’ opinions (average).
Maybe my knowledge in this field is lacking, but how can you use the average of two radiologist? Since there are no repeat measurements, and all measurements are done independently.
The single measurement (i.e. reliability of a radiologist opinion), is a relatively straight forward concept to grasp. However I am in particular struggling with the “average measurement”
I’m not sure where your confusion is coming from. You have radiologist 1, who made a rating on a patient. You have radiologist 2, who made a rating on the same patient. You add them together and divide by 2 to get an average rating for your two radiologists.
Thanks Mike! That is what I initially thought, but my professor was certain that this was not the case.
He envisioned that you have >
Radiologist made a rating on all 30 patients & then repeats the rating again.
Radiologist likewise makesa rating on all 30 patients & then repeats the rating again.
You take the average repeats of radiologist 1 and take the average repeats of radiologist 2. The icc then compares both averages to produce the average measurement*
Since the radiologists rated all the patients once, he believed that only the single measurement was appropriate in this clinical study.
Hey mike,
I have pretty much explained it concisely?
Cheers
I’m not sure whom you mean by Mike, since you’re Mike, and I’m not.
If you made repeat ratings, you would more likely calculate a coefficient of equivalence and stability, since you believe your estimate to be unstable both over time and between raters. You would not use ICC in that case.
“Single measure” does not refer to the number of observations by each rater. It refers to the number of observations from independent sources of which you wish to determine the reliability. If you want to predict the reliability of a single person making a rating from multiple people making ratings, you want “single measure.” If you’re going to take the average of your raters and use them in other analyses, you want “average measures.”
Hi. I am attempting to compute intercoder reliability for content analysis by 3 raters. The same 3 raters will be coding the data for presence of each of the 40 measures. In this case I should compute the intercoder reliability using ICC1.. Please advise which statistics I should report as the intercoder reliability and what is an acceptable level. Thank you very much for your advice.
Please! Read the whole topic, including Q&A! I know it takes some time but it is very instructional! Your design topic and suggested answer just show you did not read through ANY of this post… so your questions are gratuitous! This kind of statistics is not a one-stop option, if you think so, please stay away! Happy analyzing in the correct way!
I would actually say that because you are coding “presence” of a measure, you are probably dealing with dichotomous (yes/no) data, in which case you should not use ICC at all – you probably need either simple percentage agreement or Fleiss’ kappa.
Thank you, Assoc Professor Landers, for understanding my problem and J for your advice.
Sorry that I have not elaborated well on the issues that I faced when computing the results of content analysis conducted by three coders.
The 3 coders coded data for presence, with no presence = 0 and presence = 1.
Though we have very high level of agreement for each of the 40 measures on 200 texts (pilot coding), I am getting very strange results after running ICC1 using SPSS. Could this be due to lack of variability in codes?
Hence I sought advice on whether I should compute the intercoder reliability using ICC1 and which statistics I should report as the intercoder reliability in such a situation.
Appreciate your kind guidance.
As I mentioned before, ICC is not appropriate here. You have nominal data, which does not meet the distributional requirements of ICC. You should calculate Fleiss’ kappa (or Krippendorff’s alpha).
To accomodate all variations, please consider Krippendorff’s alpha! Prof. Landers, any ideas about this measure?
My understanding is that Krippendorff’s alpha is a general case of virtually all agreement statistics, including kappas, ICC, etc, for any number of raters and any amount of missing data. I’m not sure if there actually are any common agreement statistics that can’t be expressed as a K’s alpha (importantly, alpha does not replace consistency statistics).
There are only two problems I am aware of with it. The first is that its flexibility also makes it quite complicated to calculate, and it has different approaches depending upon scale of measurement and a variety of other factors – that makes it hard to follow when looking at formulas (just compare the formula for Fleiss’ kappa with the formula for Krippendorff’s alpha for nominal three-rater measurement). The second is that it is entirely data-driven, which occasionally causes inaccuracy – so for example, if nominal ratings are made on 4 categories but no rater used them, kappa will capture that (correctly) whereas alpha will be biased downward. But that is only a problem when you happen to have data with that characteristic.
Dear Landers,
Thank you so much for this informative article.
I have a question for you. I have assessed 30 participants on two versions (Hindi and English) of a same 36 item scale (each item has yes or no response). I need to do reliability analysis.
Can you please suggest which way i can do it. is ICC a suitable method for this?
ICC is almost certainly not appropriate, but it depends what you want to do with the means of those scales. You will most likely need to use structural equation modeling to establish measurement invariance across the two versions if you hope to compare their means directly. See “A Review and Synthesis of the Measurement Invariance Literature: Suggestions, Practices, and Recommendations for Organizational Research” by Vandenberg & Lance (2000).
Hello, thank you so much for this. I am completing a study at university where 7 assessors/judges have scored 8 videos with a colour category (one of four colours) – how is this possible in SPSS. What does the data type and measure need to be in order for this to work?? Thank you so much.
Kind regards,
Rebecca
I don’t know what you’re doing, so I don’t know. If you’re trying to determine the reliability of the color codes, you’ll want Fleiss’ kappa. I would use Excel and work through the formulas – SPSS won’t give that statistic without syntax, and SPSS syntax is clunky.
Hello Dr. Landers,
I found this site very helpful!
I just have one query. For a study I’m working on, I had three coders read a set of stories (N=82) and make judgements on 3 perceived characteristics of the writer for each story. Each coder made the same judgements about the same stories. However, one of the coders didn’t agree well at all with the other two, so I left them out temporarily.
Then, with the remaining two coders, I ran two-way random ICCs, which were .42 and .56 for two of the traits (ps<.01).
Does this indicate moderate reliability?
Is it acceptable to average across these two coders' scores for each variable?
Finally, I also read somewhere that it is not ideal to run ICCs with fewer than 5 coders – is this true?
Many thanks!
Helen
That is pretty poor reliability. Assuming you’re talking about ICC(2,2), that indicates that only 50% of the variance observed in your mean rating comes from “true” variance. You generally want at least .7, preferably closer to .9.
It depends on what you mean by “ideal.” Having a smaller number of coders, assuming all coders are drawn from the same population, will result in lower reliability. So if your ICC(#,1) is already low, that means you’ll need even more raters to make up for the limited information provided by each rater individually.
Hi Richard,
I echo all of the previous sentiments regarding your very user-friendly explanation about ICCs. I have used your guide a number of times now. Thank you very much for taking the time to write and post this. In the most recent instance of running these stats, however, I have run into a bit of an anomaly. Perhaps you could help?
We had a number of raters go into the field together and rate the same case using an established scale, so that we could determine the extent to which each rater was reliable against an established rater (before we send them out on their own). To evaluate this, I ran a two-way mixed ICC looking at absolute agreement, adding ratings of the established rater and one trainee as variables (so as to evaluate how consistent the trainee was with this established rater). I then repeated this for each trainee rater. We got good levels of reliability, however one rater with higher levels of agreement (59% absolute agreement across rated items, 14% of ratings out by 2 points from the established rater) actually had a lower ICC (.734) than someone with lower levels of agreement (38% absolute agreement, with 24% of ratings out by 2 points from the established rater…yielding an ICC of .761).
I am not sure why this should be, and if I am perhaps doing something wrong. Can you think of an explanation that could account for this? The data is technically ordinal, but it is a 7-point scale and absolute agreement is not often at very high rates. Your advice would be much appreciated.
Sincerely,
Steven
If you always have a “gold standard” rater, that means you have meaningful pairs – so in that case, it sounds like you should potentially be using a Pearson’s correlation or possibly Spearman’s rho. ICC provides the reliability of your raters _in general_, so you are capturing information about both your “goal standard” rater and your experimental rater with each ICC, which is a contaminated measure of what you seem to want to know (i.e., the reliability of the “new” rater).
As to why you might have seen the pattern you saw, it might be helpful to remember that ICC is a close cousin of ANOVA. It is basically calculated by looking at the ratio of between-case differences to between-rater differences. Between-rater differences may be relatively large in contrast to your between-case differences if the raters disagree but they might also be large if there is not much variance between cases. So that is what I’d suspect first. However you might get better information anyway by instead looking at either Spearman’s rhos or both 1) Pearson’s correlations and 2) mean differences among all raters simultaneously. The latter approach also helps you determine which particular bias is causing disagreement (e.g., leniency, severity, central tendency, or a general accuracy problem).
I calculated an ICC for my tool in which i was the same tester and did a test and re-test using the same subjects on different days. The data I collected was able to range from 0-180. After running the data I found that my reliability using a majority of the numbers was very poor, as it gave me negative ICC. this is okay data as I’m not controlling other variables as to what would make me a poor rater. However one gave me a -1.121. I was wondering how can i get a negative number over -1? does this mean the numbers were entered wrong into SPSS? have you seen this before?
Thank you for the information
Negative ICCs can be caused by very little between-case variance or very little within-case variance. It could suggest very high agreement. I would suggest looking at univariate descriptive statistics, histograms, and scatterplots to see if you can spot anything that looks odd.
Dear Dr. Landers,
I don’t need to say it but i believe reiterating that your post is AWESOME is in order:D its AWESOME!
I am currently conducting a research to develop a tool to measure moral development in adolescents. I have developed a 16-item tool, 4 factors comprise the construct(morality). I used 60 participants to a test-retest reliability. As I do not have a composite score for the tool. Doing a pearons on 16-items did not seem to make sense as such I am doing an ICC(3,1) in which the raters are my 16-items: am I on the right track?
Further more, Dr. Richard, I also used the data from the final tool to categorize the qualitative responses into a 6stage model of moral development. the numbers from 1-6 that the raters need to make correspond to each level of development; if a rater uses one then it signifies a stage 1 moral reasoning. I have data from 200 participants, i have 2 raters rating all 200 then a 5 others raters rating responses of the participants. I want to actually check for absolute agreement. and the ratings of these 7 raters are the only ratings that I am interested in. As such what ICC do i use for test for the reliability of categorization/diagnostic/interpretative criteria? also am I on the right track?
Thank you for your time.
Live in Joy
If you don’t have a meaningful composite, there is no reason to calculate an ICC – or reliability in general. ICC, like alpha, assumes a meaningful unit-weighted composite.
For your second question, it doesn’t sound like you have interval-level measurement, and categorization is not covered by ICC. You probably want some variant on kappa.
Hello Dr. Landers,
That was a much clearer description of ICC. Thank YOu.
So I have 3 different raters (surgeon, physician and radiologist) whom I have randomly selected to measure certain X ray angles. I want to know if these Xray angles measurement have a good inter rater reliability, generally.
So do I use two way random or mixed? I use the same 3 raters for all 70 cases. I guess I use ICC2.
Do I use consistency or agreement? The angles have normative measurements, so cases could either have values in normal range(130-140) or higher (140-160)if abnormal. So all raters should be measuring similar value of angles on X rays.
Single or average? There is no particular single observer I am interested in. I just want to assess inter rater reliability among 3 types of different doctors
Random or mixed depends on to whom you are trying to generalize.
Consistency or agreement depends upon whether particular numbers are meaningful or just patterns. I would imagine you would care about particular numbers re: angles.
“just want to assess inter rater reliability among 3 types of different doctors” is not a meaningful phrase. You either want to know the reliability of individual doctors, in general, or the reliability of the average rating made across three doctors. If you’re trying to figure out if the three doctors are making ratings differently, you probably don’t want reliability (or ICC) at all.
Hi Dr. Landers – I am comparing the personality assessments of two groups of raters and asking how similiar do these two groups rate the subjects on the assessments. Although the groups of raters are distinguishable (so Pearson may be appropriate), the challenge is that in some cases raters from one group evaluated multiple subjects and I believe independence is an issue. For example, in a school environment where parents and teachers may both fill out assessments for students, each parent only evaluates one student, while some teachers may evaluate several students. So if there are 60 students, and 10 teachers participating, and one teacher rates 14 students, one rates 8; one rates; 6, etc., what statistics would be appropriate for this type of scenario? The teachers all have similar experience and relationships with students. Thanks in advance for your help.
Yes, you have identified the problem – you have multilevel rating dating. It doesn’t sound like you’re interested in assessing reliability; it sounds like you just want to analyze your data. So I would not go with ICC for that. You probably want HLM or multilevel SEM (although your sample size is a little small), although it depends on your research questions and hypotheses. If your only hypothesis is to compare the groups, I would do that directly – use ICC to assess the reliability of teachers, note that you have no way to assess reliability of parents (and thus observed relationships may be attenuated), and then compare the two groups with Pearson’s.
Hello Dr. Landers,
first of all, I would like to thank you for your clear explanation of the use of ICC.
I am doing a study testing the time (measured in seconds) and the effort (Borg scale) of a sample of individuals holding on in a particular position. The Borg measure is taken directly from what the individual says after finishing the test.
After this the same individuals came a second time and did the test again.
How could I measure the reliability of this test?
Thanks in advance for your help.
It sounds like you have the same measure administered twice over time, which sounds like a situation for test-retest reliability to me. However, it depends on the nature of the test. Assuming temporal variance is the only variance you want to consider error, the specific way to determine reliability would still depend upon the scale of measurement of your test.
Hello Dr. Landers,
thanks a lot for all these helpful answers. I plan using the ICC for rather uncommon comparisons and therefore still struggle with knowing if my calculations are valid or not.
Briefly, I plan on comparing two distinct methodologies, which are hypothesized to measure the same construct (on interval level) on the same sample.
So far I conducted a two-way-mixed model, with absolute agreement. Now I want to find out if my two methods significantly agree and come to the same outcome.
Could you tell me if the ICC is an appropriate measure for my calculations at all?`
Thanks for your help!
Reliability analysis is not really a great way to do what you’re talking about, ICC or otherwise. It is not a sufficiently powerful toolkit. If your hypothesis is about construct validity, you’re probably going to want to learn a technique called “measurement invariance testing.” It does all of the many analytic steps you’ll need to do to make your measurement claim but in one analytic framework. I suggest starting here: http://orm.sagepub.com/content/3/1/4.short
If you want to continue using a non-SEM approach, you’ll need to establish construct validity some other way. The most common approaches are multitrait-multimethod matrices (MTMM), which is the older way, or confirmatory factor analysis, which is the newer way. But if you’re going to do a CFA anyway, I’d say you might as well do full measurement invariance testing. It is not much more complicated.
Hello Dr. Landers,
in my study three 20 ratees were interacting with a dog for 15 minutes. These interactions were recorded and rated by three raters afterwards. All three raters rated every video. The ratees were rated in terms of a scale consisting of 7 items (describing for instance verbal interaction or petting the dog) ranging from 0=none to 10=well marked. Every item was rated thrice, after 5 minutes, after 10 minutes and after 15 minutes. How do I compute ICC?
Thanks in advance!
Mike
Mike, start out by thoroughly reading this exact tutorial a
So it sounds like you have a 3 by 3 matrix, 3 times by 3 people, 9 ratings per subject? In that case, you would need to calculate ICC manually by adapting the formulas presented by Shrout & Fleiss or using a hierarchical modeling program that calculates ICC for you (such as HLM – book here and software here). SPSS won’t do it.
Importantly, to use ICC here, you are assuming that differences over time are solely measurement error. If you expect population-level changes over time, then ICC is not appropriate as a summary of the full dataset – you’d want to calculate three ICCs, one for each time point, which can be done in SPSS (sounds like some type of ICC[2] from what you wrote).
No, not exactly. I have 20 videos (because I have 20 ratees) lasting 15 minutes each. And three raters who rated all the videos each on a scale consisting of 7 items. The rating was conducted as follows: after the first 5 minutes (first interval) of watching one of the recorded videos, each rater had to rate all the seven items. Then, after having watched the next 5 minutes (second interval), all raters rated the seven items again. Finally, after having watched the last 5 minutes (third interval) of a video, the raters rated the for the third time.
So if by “conditions” you meant items, it is not two conditions but seven.
Dear Richard,
Thank you for your very useful page about ICC. Since I have dichotomous data, I am a bit confused if I am able to use the ICC after reading your comments on earlier questions.
I have 3 raters on all the items. All items are scored sufficient (1) or unsifficient (0).
Do you think I can use the ICC? If not, do you have a suggestion for another measure? I read about the Fleiss kappa in an earlier comment.
Thank you in advance for your response.
Marjoleine
Since you can conceptualize dichotomous data as either present (100%) or not present (0%), that is ratio-level measurement, so you could calculate ICC on dummy coded dichotomous data. However, because the normal distribution of scores is missing, you will end up with a conservative (attenuated) estimate of reliability. Since you have three raters, I would recommend Fleiss’ kappa.
Prof Richards, to me this would seem like a perfect opportunity to apply Krippendorff’s alpha since it can handle multiple raters, all type of measurement levels and is quite robust to missing data as well. Could you provide a brief comparison of the benefits of either two tests? Thank you!
Krippendorff’s alpha can be used in essentially any situation requiring an assessment of interrater agreement, regardless of both rater count and scale of measurement. If you only require interrater consistency, it will be a conservative estimate. The only other disadvantage is that it is more computationally complex than other statistics – for example, ICC can be calculated from an ANOVA summary table, and kappa can be calculated from a simple contingency table.
This complexity stems directly from its general applicability – any statistic that can be used in a wide variety of situations is also going to require greater expertise to know how to measure it in a particular situation.
Thank you for providing such great information. I asked a question earlier about kappa v. ICC and you directed me toward kappa, which was very helpful. A reviewer is asking for weighted kappa instead, but I dont think it is appropriate because the data are dichotomous, not ordinal.
In a nutshell, I have two raters and they are determining if a disorder is present or absent according to DSM5. Kappa is based on the single overall variable, just present or absent. Each rater also scored a patient on the presence or absence of 10 subcriteria which did not figure into the kappa analysis. Weighted kappa would need to be based on the sub criteria (so 10 variables per patient, completed by each rater), but each score is also a dichotomy, present or absent. Can weighted kappa be calculated? If so, how? Is there a calculator on line? SPSS doesnt do it. Thank you for your help.
A weighted kappa is calculated by assigning weights to different levels of disagreement. You don’t necessarily need ordinal data for it, but you do need more than one type of disagreement (to weight them differently). As I understand it, you only have two types of agreement (1/1, 0/0) and one type of disagreement (0/1), so I don’t see any way you could assign weights meaningfully that would give you an answer other than what an unweighted kappa already tells you. I would recommend reading this for some context – it’s pretty easy in Excel, if you do end up needing it: http://www.real-statistics.com/reliability/weighted-cohens-kappa/
This would seem like a perfect opportunity to apply Krippendorff’s alpha since it can handle multiple raters, all type of measurement levels and is quite robust to missing data as well.
Hi! Me again, on this same issue of weighted kappa. The reviewer is insisting I calculate weighted kappa. Just to recap, I have two raters who scored 50 cases on 7 different dichotomous variables. If 5 of the variables are scored 1, then an overall category is scored 1, if not, 0. Originally I computed kappa as a measure of agreement between two raters on the overall category. The reviewer wants me to create an ordered variable by summing each of the seven dichotomous variables. So now for each case instead of a 1 or 0, each rater will have a “score” from 0 to 7. Following the example you referred me to above (real stats in excel), I am unclear how to proceed. I assume that each rater now has 8 responses (0 to 7), but how do I assign weights? A score of 2 is just as meaningful as a score of 7, especially if raters agree. Any additional guidance is appreciated.
I don’t use weighted kappa myself, so you’re going to want to find a source describing what to do in this situation. My intuition would be that you’d weight a single-rank disagreement as 1 and then weight further as the distance increased, e.g., a 0-rank disagreement as 0, a 2-rank disagreement as 2, a 3-rank disagreement as 3, etc. In the Excel approach I sent above, that basically means your diagonal (top left to bottom right) would be 0, first line out from it in either direction 1, then 2, then 3, then 4, etc. Then if one person ranked 0 and the other 7, that would be captured as extreme disagreement with a hefty weight. But I don’t have a cite for that particular approach. If the reviewer is suggesting this is standard procedure, I imagine there’s a prominent source somewhere that provides guidelines.
You might also think about Jan’s Krippendorff’s alpha suggestion as a “better” solution given that type of data, although suggesting a better approach to an insistent reviewer is always a bit of a gamble.
May I be clarified if I can compute for ICC and how I can compute it if I have 2 sets of taters. The research is on determining reliability in measuring certain parameters about teeth between a teachers and students The taters are a teacher and group of students, the teacher would measure all the teeth of patients while each student would be measuring only 1 patient.
Also, in the result of ICC, there is the computed Cronbach’s alpha. Should I also report this value? Do you have range for the Cronbach’s alpha and the ICC and their verbal interpretation? Thank you very much.
You’re using the mean of all students and all teachers together, assuming they are all drawn from the same population of raters? If so, then it sounds like ICC(1). You would not normally calculate alpha in this case. I don’t know what you eean by “do you have range”, but I like reliability to be above .8, if at all possible.
Thank you very much for your immediate response. Since I am computing for the ICC for each teeth, there are results which are not .8 and above. Suppose I get .23 or .45 value of ICC, how would I interpret these values then. Thank you very much for helping me understand ICC better.
Then that means only 23% of the variance in the ratings can be explained by actual variance between patients. That is a very unstable rating, and I would not use it in future analyses.
Hi Dr. Landers. Thank you for this well-written and informative article. I have a question regarding interrater reliability with missing data. In my study, I have entries from 2 raters that I need to compare. The raters were asked to rate heart rate patterns (4 different patterns), however some entries are blank since the rater could not judge the pattern. But if rater A rates a given pattern as pattern 1, and rater B decides that he can not accurately judge the same pattern, isn’t this important information that would affect reliability? The problem is that spss eliminates these missing data. I am wondering If I can use spss to calculate interrater reliablity without eliminating these unidentified cases.
I am looking forward to reading your suggestions!
Any sort of analysis like this, with deletion approaches or even with imputation, will assume missingness at random (MAR) or missingness completely at random (MCAR). If you have not missingness at random (NMAR) then you are right to worry, although the right approach to deal with it is dataset-dependent. I would recommend you read up on these terms and figure out what is most appropriate for your particular case.
Dr. Landers,
Posting again on the same analyses because my reviewer has raised yet another question. I am calculating two ICCs. 1) to compare reliability between two raters who are each using a different diagnostic method to complete a DSM-5 diagnosis. The variables are the sum of all the criteria for a given disorder. That is, this disorder has 7 symptom criteria which are scored 1 or 0. The variable I am using to compute ICC is the sum of those variables; so for each ratee (or case) a score in this single variable could be a number from 0 to 7. The same method was followed for both diagnostic methods being compared. There was only 1 rater for 1 diagnostic method and 1 rater for the other diagnostic method. From your instructions above, I see this as ICC(2), two-way random, mean reliability, and absolute agreement?
For the second ICC, I am comparing the results from 1 rater using 1 assessment method to results from 10 different second raters, but each second rater only scored 5 cases each. Thus, I am comparing 50 ratings from rater 1 to 50 ratings from rater 2 (this is one variable, but it includes scores from 10 raters). I assume this is ICC(1) because of the multiple second raters, but I am not sure because it is not multiple raters per case. Please advise on what you would do for each situation. Thank you again for providing such a great resource.
If you’re conflating diagnostic method and rater, I’m not sure I can see a way that analysis would produce a useful result. ICC(2) would be correct only if you assume those two diagnostic approaches to be a random sample of a population of diagnostic approaches as well as those raters as a random sample of a population of raters. But even then, you can’t disentangle the rater effect from the approach effect, since you don’t have replication of either rater or method. So you are making a lot of assumptions that aren’t usually justified.
In the second case, this doesn’t really sound like a reliability question. It sounds like you want to compare if your 1 rater is systematically different from your group of 10 raters. In that case, you’d want ICC on the secondary raters only (hopefully there is replication there) and then see if your lone rater’s variance can be explained by your secondary raters’ variance. In that case, ICC tells you how consistent your secondary raters tend to be, and your main analysis (t-tests, in the simplest case) would tell you how likely is it that the lone rater and your group of raters produced the same mean, assuming that they would otherwise be in complete agreement.
If you do use ICC(1), you are again making a lot of assumptions – one, that there is no systematic rating effect by the lone rater, two, that the lone rater and the secondary raters are all drawn from the same population of raters, and three, that there are no rater x target interactions. Again, usually not justified, but perhaps this is more common in your literature – I don’t know anything about these raters, myself. But it seems like it would require a lot of theoretical justification.
Hi Dr. Landers, thanks for your response on my previous question! I’m back with another 🙂
We have developped a voice-assessment training-tool and want to evaluate its effectiveness for training. Calculating ICC for intra- and interrater reliability before and after training is a logical choice, but how can we determine if the ICCs before and after differ significantly (or not)? Could you give us your thoughts? Thanks again! Jan
I have never needed to do that before myself, but I believe you’d need this technique: http://conservancy.umn.edu/bitstream/handle/11299/120038/v18n2p183.pdf
Dear Dr. Landers,
Thanks for putting this site together. It has been very helpful in many ways.
I have a question about comparing the ratings of 5 raters with an expert rating (gold standard). All raters, including the expert, watch the videos that depicted performance of a motor skill. They used a scale from 1-4 to rate levels of performance.
I used icc to assess inter-rater reliability as per instructions found here. How would I go about assessing consistency of ratings between the 5 raters and the expert?
I thought about using the median score of the 5 raters and compare with the expert rating. But thinking here, this is more of a measure of association, am I correct? Another way is to do pair ratings (1 x expert, 2 x expert, …) and then average the 5 pairs; I am not sure on this one either.
Any help would be greatly appreciated.
JP
I think it’s important to reconceptualize what you’re doing here.
You have two populations – a population of experts and a population of novices.
From the population of experts, you have drawn a sample of 1. You assume this expert to be 100% reliable, so you only need one person in this sample to get a stable estimate of experts, in general.
From the population of novices, you have drawn a sample of 5. You don’t know how reliable these novices are (i.e., how consistent they are with each other), nor do you know how valid these novices are (i.e., how consistent they are with the experts).
To that end, you must first demonstrate that you have adequate reliability in your sample of novices in order to draw conclusions about novices, in general. This is how you use ICC first, and you want an ICC(2,5) to determine the reliability of the novice mean.
You could theoretically also use ICC to assess the reliability of your sample of experts, if you had more than 1 of them. But you don’t because you’re assuming the expert is 100% reliable. If that isn’t true, you should get more experts.
Now that you have a stable estimate of expert ratings and a stable estimate of novice ratings, you need to provide evidence of convergent validity. This can be done many ways depending upon your sample characteristics and research goals. Since you’re using ICC, this implies to me that you have interval or ratio level measurement (otherwise, ICC would be invalid). Thus, you could calculate a Pearson’s correlation between the expert score and the novice’s mean score to see the extent to which the ordering is consistent between the two.
However, a Pearson’s r can still be strong with absolute differences between the two cases contrasted, so if absolute differences are important to you, you should use something else. For example, you could calculate an ICC(2,1) requiring absolute agreement using those same two values (expert ratings and mean novice rating). However it’s important to note that the ICC in this case is not a reliability estimate – it’s a validity estimate.
If you are interested in the correspondence of the mean scores, you could calculate a Cohen’s d to compare the two, or even a paired-samples t-test. It all depends upon your specific research goals.
Hope that helps!
Hello Dr. Landers,
Thank you for providing such an excellent reference document!
I do have a question about computing ICC. I have been asked to compute ICC2 for individual task statements across 76 raters. In other words, I am being asked to estimate the inter rater reliability of 76 raters for each individual item/task statement. My data is structured so that each item represents a row and the raters’ response to those items are in 76 columns.
I receive the error message that there are too few cases (n=1) when I try to run the analysis. I assume ICC is not the appropriate method to estimate reliability in this case, but am unclear exactly why. There is variability across raters for each item and it makes sense that we would want to get an idea of how much the ratings vary for each task statement. I am thinking that rwg may be a good substitute, but in this case I am being asked explicitly to use ICC. Any insight you can provide would be greatly appreciated.
Thank you!
Alli
If you can conceptualize task statements as cases, then you would have n=number of task statements. That would be my guess as to what the reviewer is asking for, at least. But any ICC(#,76) should be extremely high just due to the math involved, so that’s a bit of a weird thing to ask for.
Thank you much Dr. Landers,
I decided to use the ICC(2,1) – absolute agreement. Should I report the Cronbach’s alpha along with the ICC values? If so, what would the interpretation in this case?
Thank you in advance.
JP
If you’re talking about using both ICC(2,5) to estimate the reliability of your novice mean and ICC(2,1) comparing your novice mean with your expert rating as convergent validity evidence, you don’t need any additional reliability estimates (including alpha) – the ICC(2,5) is your reliability estimate for the novice mean. You are assuming perfect reliability in the expert rating.
Hi Dr.Landers,
thanks a lot for such a useful reference!
I am concerned about one result I obtained while running an ICC2 (two way random) for a test retest reliability study. I created a tool to assess the nutrition environment inside supermarket and did a small test-retest study on a sample of 6 supermarkets. For most of the items I assessed, the ICC is pretty high, but for one item in particular (price of a chosen product), I obtained -2.137. I understand that this result is simply not valid, but I can’t seem to understand why…
There was not a lot a variability in the 2 sets of data, but we could make the same observation about other items studied and the ICC for these was above 0.9…!
Thank you a lot for your help
It all depends on the particular ratio of within-group to between-group variance. If the ratio is particularly lopsided (e.g., 1 disagreement among 100 possible agreements), ICC can turn strange. If your agreement is that high, I would suggest using simple percentage agreement (or if appropriate, chance-corrected percentage agreement, which is a Cohen’s or Fleiss’ kappa) as your reliability estimate instead.
Hi Dr. Landers,
Thank you for providing such valuable information.
I am developing different animal personality research and have always worked with just one sample, therefore it has never been a problem for me to do the ICC. However this time I have two diffeerent samples from different chimpanzee sanctuaries and they were rated by 12 and 6 raters, respectively. I don’t know how to insert data on SPSS.
I tried two different options but in both cases got the following message “There are too few cases (N=0) for the analysis” so SPSS is trying to evaluate the empty columns (the difference between the 12 and the 6 raters). I cannot find the option to say SPSS to evaluate the first 12 columns and the 6 following ones rather than all the 12 columns like it does.
Therefore I ask to myself if I probably should have to press any option on SPSS or even insert data in another way…. What should I do? Any ideas?
Thank you very much in advance!
Kindest regards,
Yulán
I’m a bit confused by your description. Your analysis implies all 18 raters rated the same set of cases. Is that right? If so, you have variable numbers of cases per line and will need to calculate ICC manually. If you’re saying that 12 raters rated the cases as their sanctuary and 6 raters rated the cases at their other sanctuary, as long as you’re comfortable saying these all come from the same population of raters and the same population of chimpanzees, you can combine them into a single dataset and calculate ICC(1) – but you will also need to do that manually. The basic approach in SPSS is to conduct an ANOVA predicting your outcomes from case numbers, then use the formula (MSB- MSW)/(MSB+ (n-1)*MSW)) to calculate ICC(1,1). You can then use the Spearman-Brown Prophecy Formula to calculate ICC(1,k) (you are essentially forecasting reliability for k raters given the reliability of 1 rater).
I thought ICC could be used to determine correlations between measures which violate “independent samples” assumption. My data are 8 measures at each point with 290 points; but the points include longitudinal data from 65 participants (3-7 observations per participant). I’m trying to figure out which of the measures are basically redundant (maybe the between-subject ICC?), but I’m having trouble converting your inter-rater reliability example to my data set. Can I even do this in SPSS? Any help would be appreciated.
It depends on what you think is consistent and where. If you are expecting changes over time, then you anticipate temporal variance reflects true score variation, not an unreliability problem, so you will want to analyze each time point individually. In such cases, people sometimes report average ICC over time. If you think temporal variance does in fact reflect measurement error, then you can still calculate a single ICC in SPSS, but you’ll need to do so manually – SPSS requires equal cell sizes to run its analysis, so it won’t do it using the click interface (see other comments where I discuss running an ANOVA and hand-calculating ICC from the output). Once you have that ICC, you can calculate how many time points should be necessary in the future to get a stable estimate of whatever it is you are measuring.
Having said all that, ICC assumes independent sampling. You can’t test for it using ICC; you need to rely on existing theory regarding your construct to make that decision. For example, if you were measuring personality 7 times, there’s no reason to think personality true scores shift around by time point, so temporal variance is likely unreliability and should be treated that way.
Thank you so much for this excellent article! It’s extremely helpful to me!
Why is it that the ratings of my raters are too close to one another but they still have an ICC value of zero? Isn’t it supposed to show a high level of agreement since their ratings are approximately the same?
For instance, here’s the sample data.
Criteria…..Rater 1…..Rater 2…..Rater 3
…..1…………..5……………5……………5
…..2…………..5…………..4……………5
…..3…………..5…………..5…………….5
…..4…………..5…………..4……………5
ICC is at its core an effect size expressing a ratio of variances. In your case, Rater 1 and Rater 3 have identical ratings which are all 5s, so there is neither between-rater variance nor within-rater variance. That will throw off ICC dramatically. In such cases, you would want to use a simple percentage agreement (or chance-corrected percentage agreement if feasible) instead.
Remember, ICC is not simply an estimate of “how reliable your scale was”, just as coefficient alpha isn’t, or any other approach. They are all _estimates_ of the proportion of true to observed variance, and thus require specific assumptions to make those estimates (since there is no way to actually know what true variance is present).
Can the SD for each criteria be used instead of the ICC then get the average of the individual SDs?
That has very little to do with reliability.
Instead of ICC, can we use the SD of each criteria then get the average SD of all criteria?
As I said, that is not a reliability estimate. You are just assessing how well scores cluster within items, which is not the same.
Hi, I didn´t read al the comments but I found your post very helpful. However I still have one quarstion regarding doing ICC in SPSS…
I chose the appropriate (I think) choices under statistic but I am not sure what method I have to choose in the original “window” under “Model”. I have a choice between: “alpha”, “splitt-half”, “Guttman”, “Parralell” and “Strict parallel”. The automatic option is “alpha”. When would you choose which “model”?
thanks
That analysis is separate from the ICC analysis, so it does not matter what you select.
Hi Dr Landers,
I have tried reading through the comments to avoid asking a redundant question but was hoping to ask a quick question to be sure that i am performing the correct calculation.
I am testing the reliability of a new scale. I am using the same 3 raters to score the same 200 clips of a procedure using an 8-point scale. i am interested in absolute agreement
Do i calculate a two-way, random average measures ICC for absolute agreement? Is this referred to as an ICC (2,1)?
I then have one of the raters performing a second rating of 100 clips. I want to assess intra-rater reliability using these 100 clips. Do i use the same ICC or a Pearsons for this?
Thank you in advance.
A.Beth
You have described it correctly, but that’s an ICC(2,3). For intra-rater, you’d be calculating an ICC(2,2), which is identical to a Pearson’s if calculated as a consistency type. If you want agreement, you need the ICC specifically though.
Thanks so much for taking the time to clarify.
I then have 40 participants rate the same 10 clips, looking at agreement post training in scale use.
I should calculate a two way random average measures for absolute agreement, would this be an ICC (2, 40)?
Am I correct in assuming i can’t then compare agreement from the first arm of the study to this reliability score?
Thanks again,
Alex Beth
So to be clear, your goals are to 1) assess the reliability of your experts and then 2) to assess the reliability of novices post-training? If so, you will want to put them on the same metric, which would be ICC(2,1), i.e., the reliability of a single person making ratings in isolation. ICC(2,3) among your experts is the reliability of the mean rating calculated from all three expert ratings, not the reliability of an expert. If you calculate ICC(2,1) for your experts and also for your novices, you can compare them directly.
yes, exactly. looking at the reliability when the new scale is used by different raters, and with different levels of training. thank you so much for your help. I will calculate an ICC (2,1) for each study arm. Does this mean I would describe it as a two-way random single measures ICC, instead of average measures?
thanks again, Alex
Sorry, I mean ICC(1,1) for the novices – you don’t have a consistent person effect. They are still comparable though.
Hi Dr Landers,
Thank you for the informative post.
I have a question regarding using ICC for twin study. I have set up the database in spss in which each row contains data for a twin pair. Then e.g. column 1 is body weight of twin a and column 2 is weight of twin b respectively. So I run the ICC choosing 1-way random. To look at the concordance of body weight between each twin within a pair, I should be looking at the single measures ICC right?
Single measures will tell you to what extent each twin’s weight corresponds with a hypothetical “average twin” true score within each pair. So if that’s what you mean by “concordance,” then yes.
Just a late follow up question: So what do the average measures mean in my scenario?
I don’t know your area, but I suspect it isn’t interpretable.
Hello Dr. Landers
Your post has cleared up many questions I had about ICC and I was hoping you could answer one nagging question I can’t seem to find an answer to and provide some guidance.
In the past I have worked for psychologists who have used ICC as a quick way of determining how similar “true scores” (correct/agreed upon scores) on a measure were to a rater’s scores. For example, they would run an ICC analysis comparing 54 “correct/true” scores on one measure of symptom severity (rated along a 4-point continuum) to a rater’s scores. The aim was to tell if the rater was doing an acceptable job of completing the measure and accurately profiling the individual as one would expect.
Running it in SPSS, a two-way mixed, consistency, single measures ICC was calculated between the “true score” and a single rater’s scores. I can’t seem to find any resources which indicate ICC being used in this way. Can ICC be used in this way?
I ask because I was hoping to do something similar in a study I am conducting. I am aiming to screen participants in my study based on how well they performed in a learning task. Participants completed a learning task where they were intended to decipher the approximate probability of 10 letters being followed by a loud noise. In this way, they form subjective rankings for the order of letters from least likely to be followed by a loud noise to most likely. The task is designed in a way that it is very difficult to learn the true probabilities of a letter being followed by a noise, however participants should be able to relatively rank the probabilities accordingly. They indicate along a continuum from 0 to 100% how likely they believe each letter is followed by a loud noise.
Given what I had known about the use of ICC, I had aimed to use ICC to screen if participants had performed adequately in the learning task. It is very likely that there will be a lot of variability between rankings, with some participants giving some probabilities that are quite removed from their actual probabilities. I am more interested in looking at all scores together and seeing if together they roughly agree with the true probabilities.
I had planned to use a two-way mixed, consistency, single measures ICC to remove any participants with ICC scores below 0.80 from analysis of a task which depended on participants having learned the letter probabilities adequately. Is this the proper analysis to use or would you suggest some other method?
Many thanks for any help you could provide and apologies for being verbose!
ICC essentially assumes that all scores are estimates of a single true score. So an ICC in that sense will overestimate novice-rater reliability. For example, if the expert said “3” and the novice said “1”, it would estimate the true score of that case as 2, with each rater being 1 away whereas the reality is that your novice is much more inaccurate and your expert is not inaccurate at all (assuming you have reason to believe your expert is perfect). If your novices and experts have very similar scores anyway, you’ll end up with >.9 reliability, and that distinction doesn’t really matter – the ICC just shows that everyone rates about the same, so the error is small. But as ICC decreases, then that gap will get bigger. It is not a technique I’d recommend, personally – the better technique is using structural equation modeling-based measurement invariance testing, which allows you to draw conclusions about much more specific aspects of disagreement (e.g., do the rate the same in terms of factor structure, in terms of means, in terms of variances, in terms of factor loadings, etc). ICC is a very blunt tool, in that regard. The same is true in the case of specific raters – you really want to compare raters in terms of shared variance (correlations) and mean differences (t-tests, ANOVA), at least, if you want to identify which of your raters is “bad” and why.
Hi Hi Dr Landers,
Thank you so much for your helpful site. For a point of clarification, I am calculating Inter rater reliability for a categorical variable (public, private, neither) for a scale I am creating from qualitative data, in this instance should I use Fleiss kappa since I have 3 coders or is Cohen’s Kappa valid? In some articles I saw that percent agreement is valid, how do you feel about that? Also if Fleiss’ kappa is really low is there anyway to boost that value?
Thanks,
Liv
Cohen’s kappa is just a percentage agreement between two people, adjusted for chance agreement. So if you have 2 people guessing at random when categorizing cases between “yes” and “no”, there’s a 50% chance they will agree purely by luck. Cohen’s kappa adjusts actual agreement for that luck factor. For that reason, Cohen’s is generally considered very conservative, because 50% assumes _pure_ luck, whereas there are probably other meaningful factors involved. Percent agreement is thus the very liberal version of that statistics, as it assumes there is no luck at all. Cohen’s kappa also allows for weighting such that “bigger” disagreements can be counted mathematically instead of just saying “agreed” or “disagreed” (this is the difference between “unweighted” and “weighted” kappa).
Fleiss’ kappa is a different statistic altogether which assesses agreement across any number of raters and is similar to Cohen’s unweighted kappa. So it sounds like you want Fleiss’.
If Fleiss’ kappa is low, it implies that you have disagreement and thus unreliability. Unreliability has a lot of unexpected effects but usually 1) makes your effects smaller and 2) makes it more difficult to attain statistical significance. The best remedy is to have your raters do all of their ratings again but with a better system of making judgments and rating calibration efforts, if you didn’t do that the first time.
I have 9 judges that rated 56 observations, 15 of these observations are coded as 0 or 1 (the rest are continuous). What model do I use?
Alex,
If your science has the same level of clarity and willingness to read, understand and work, you better quit your day-job. Please provide the necessary info for us to make useful comments, you will find these by reading through the excellent text (answer the 3 questions!) and I urge you to read through the comments…
Jan
Hi Dr Landers,
Thank you for your wonderful article. I have 2 questions to clarify here, if I could get your comments:
I am conducting a study to examine the psychometric properties of a self-administered scale (18-items, 5-point Likert scale). 200 participants completed the scale, and repeated the scale 1 week later. Then I calculated the ICC (two way random effect). Should I quote the “single measure” or “average measure” of ICC?
Separately, I have 2 scales each giving me 3 categorical outcomes. I will like to measure the agreement between these 2 scales (3×3). Could I use ICC and which type of ICC to use?
Thank you
TM
If your goal is to generalize to people using the scale in the future that don’t administer it twice, single measures, since that tells you the reliability of the scale measured once. Average measures tells you the reliability of the mean of your two measurements, i.e., if you gave the scale twice and used the mean score between the two administrations.
Categorical outcomes are not a good choice for ICC. You will want some sort of kappa, most likely. The exception is if your categorical outcomes are binary (true/false) and are dichotomized (i.e., they represent an underlying continuous distribution of scores). If so, you could calculate a mean for each scale and then use an ICC, using the same guidelines I posted here.
Dear Dr Landers,
Thanks for your excellent article.
I want to evaluate the reliability to estimate the location of the hip joint center from medical images. Two people (raters) did the whole process. The joint center is defined by x, y and z coordinates and the difference in joint center location between rater 1 and 2 can be calculated as square-root of ( (x1-x2)^2+(y1-y2)^2+(z1-z2)^2 )
Do I have to calculate ICC for each coordinate direction (x, y and z) or is there a way to calculate one ICC for the estimation of the hip joint center location?
Thank you very much.
Hans
I don’t think calculating reliability of X, Y, and Z separately captures what you are interested in knowing. The degree to which raters agree on those scales doesn’t seem meaningful by itself. I don’t know of any method off-hand, but I suspect you could use a polar coordinate system more meaningfully, i.e., do they agree on the direction from the center of the image and how far from the center (two ICCs). But that’s a guess – you should really talk to someone in your area.
Hello Dr. Landers
thank you for this very well written article on ICC. I went through your answers to the questions but am not confident about the right choices for my situation: The aim of my research is to analyze inter-rater and intra-rater reliability of teachers’ assessments of math tests from 5 students (the same test for all the students). All of the 11 teachers assessed all 5 tests (max = 38 points). After a month they assessed the same tests again. I am interested in a single teacher as well as the whole group (sample). I find ICC appropriate for the analysis but am not sure about the models. I will highly appreciate any suggestions.
Thank you
Mojca
You can analyze inter-rater reliability at each time point by analyzing one time point at a time, either ICC(2,1) or ICC(2,11) depending on what you want to do with those scores. You’d have one estimate per test. Intra-rater is harder – I believe you’d actually want something like rwg for that, but I’m not as familiar with it. All of those are analyses of the sample though.
Thank you for the swift answer. However, I am not entirely sure I understand what you mean by ‘one estimate per test’. I created a data set with 11 columns (representing raters) and 5 rows (representing tests). Do you mean I should calculate ICC for each of the 5 tests separately (by transposing the matrix)?
Hello Dr. Landers
Thank you for your informative and much needed post! I hope by now you’re not sick and tired of fielding additional inquiries (!):
I would like to use the ICC as an indicator of agreement between patients and their physicians on items of a survey measuring satisfaction with videoconference therapy sessions. The survey items are rated on a 5-point likert scale. The sample includes 60 patients- each of whom completed 1 survey in reference to a specific therapy session- and 11 physicians- most of whom completed multiple surveys, and each of which correspond with a specific patient survey (i.e. are completed the same therapy session in mind). I’ve seen studies with similar designs where the ICC has been used as a measure of agreement. My concern is that individual ratings among physicians are clearly not independent, and I do not know to deal with potential clustering effects within the context of computing and interpreting the ICC. Any recommendations on how to proceed would be GREATLY appreciated. I will be using SPSS for this analysis.
Thanks very much.
All the best,
Nick
The most straightforward way of approaching it is to ignore the nesting problem (assuming your patients and physicians all come from the same general pool of raters) and use ICC(1). To the extent that there are physician-specific effects, your ICC will likely be attenuated, but that is the best you can do without explicitly modeling it.
To be clear, explicitly modeling these effects is the better option. But that would require multilevel modeling of some sort (not a reliability question anymore, although you could do it in a generalizability theory framework).
Thanks for your prompt and helpful reply.
Dear Dr Landers,
I would like to get your input on the following:
I used 4 models to predict daily temperature over 1 year in 100 cities. Therefore the dataset comprised for each of the 100 cities 365 estimates of temperature x 4 models.
My interest is in :
1- the overall absolute agreement between the models;
2- the absolute agreement between these daily predictions at the city level (with the aim to identify cities with best and worse agreement).
It is unclear to me what type of ICC would be best and how to proceed to account for the fact that within a city daily predictions are correlated in time.
I was thinking toward a 2-way mixed-effect model, in which the predictive temperature models would be treated as fixed-effects and cities as random-effects but again I do not know how to handle the temporal correlation.
I will be using R for my analysis.
Thanks for your help.
It depends a bit on what you’re doing with those numbers. The concept of reliability only really applies when you have multiple (unbiased) sources providing an estimate of a single population value. So, for example, you would want to know the reliability of temperature across models on a particular day.
What you are describing is not really a reliability question – you want to be able to understand and partial out the effects of both nesting and time from a latent conceptualization of cross-model accuracy. That requires several additional assumptions that you don’t normally deal with in reliability estimates. So I would recommend in this case either examining this question in a bi-factor framework (i.e. structural equation modeling, which can be done with lavaan in R) or a generalizability theory framework (not sure how to do this in R; I only know of these: http://link.springer.com/article/10.3758/BF03192810). The advantage of either approach would be that you could identify precisely how much variance is explained by each source, rather than needing to collapse across categories (in which you could lose a lot of useful information/accuracy).
Say I compute the ICC using the irr package in R as follow:
icc(ICCdata, model = c(“twoway”), type = c(“agreement”), unit = c(“single”), r0 = 0, conf.level = 0.95)
, where ICCdata is a matrix with “methods” as columns and “city-day” as rows.
Would this be correct to assess the reliability (absolute agreement) between predicted temperature across models on a particular day (and city) ?
There 3 levels in my data structure (i.e., method, city and day) and my concern is not adequately accounting for the data dependency, thus leading into a biased ICC estimate.
Thanks again for your input.
I haven’t used irr, so I don’t know if your code does what you claim or not.
But if that is a normal ICC, then you do seem to be collapsing across multilevel data. As I mentioned before, that’s no longer strictly a reliability question. You would want to model each source of variance explicitly using structural equation modeling or generalizability theory.
If you are willing to assume that reliability does not interact by day and city (i.e., that no days are harder to predict in some cities), then you could used ICC(1). But I suspect that is not a safe assumption.
Hi Dr. Landers,
I am looking to calculate inter-rater reliability, and specifically ICC, among two raters who observed the same children’s social interaction behaviour. They measured the number of times each child engaged in different social interactions (i.e., positive, negative, other).
My questions are as follows:
1) Can I use ICC even though I don’t have a nominal or ordinal variable = essentially the number of behaviours that could be coded is infinite (not on a Likert-type scale or discrete categorical variable)?
2) If so, do I then calculate an ICC for each separate behaviour? According to your suggestions above, I’ve been using the two-way random ICC, specifying ‘consistency’.
3) Would I look to the single-measure or average-measures ICC value, if I ultimately want to average the two scores (if they are high-enough of an ICC that is)? I am thinking it’s the average-measure, but wanted to get your opinion.
Thanks in advance for your assistance.
1) ICC is only for interval or ratio level data. It can only be used on Likert-type data if you are comfortable assuming Likert-type scales are essentially interval. Counts are fine, but ICC will be attenuated to the extent that your counts are not normally distributed. If your data are severely non-normal, I would recommend a kappa.
2) Yes, if you’re using each behavior separately in later analyses.
3) If you want to know the reliability of an average, you want average-measures.
Hi Dr. Landers,
Thanks for your reply – however, all the information I can find on kappa discusses the fact that it needs to be a categorical variable. Given that my data is continuous looking at observer’s rating the frequency that individuals’ engaged in a behaviour…if one observer indicated that the person engaged in the behaviour 14 times, and the other observer indicated that the person engaged in that same behaviour only 13 times — it’s likely to show low reliability, even though they are very close.
Do you have any suggestions or resources of where I can find information to assess interrater reliability for data where the number of observations ranges from 1-30 and is not categorical?
Thank you in advance.
It doesn’t sound to me like you have continuous data – it sounds like discrete ratio-level data (i.e. counts). Unless your observers can record fractions of behaviors, anyway.
Statistically, you must treat it one way or another. Either you expect the counts to be essentially interval and normally distributed so that you can use ICC, or you don’t assume that and use kappa instead.
If you do use kappa, you probably want the weighted kappa variation, where differences that are further away are weighted are more significant sources of disagreement than differences that are closer. For example, you can weight disagreement such that a difference of 1 point will penalize kappa much less than a difference of 5.
Dear Dr Landers
First of all, thanks for your comments and recommendations in this site. Very helpful!
I hope you can help me with my question. I’m using the Krippendorff’s alpha for reliability.
I have 3 groups of observers: G1= 2 observers, G2=4 observers, G3=8 observers, assessing 20 units. I want to calculate the intra-class correlation (ICC) to provide the reliability of my observers (convergence among my interviewees).
Do I have to calculate this for every group (G1, G2, G3)? I have similar results for the three groups (k-alpha=0.73; 0.71; 0.69)How can I provide a general assessment for the whole set (3 groups)?
Perhaps an average taking into account the three results?
Thanks in advance for your assistance.
Regards
Why can’t you just consider them 14 observers? If group membership shouldn’t affect reliability, the groups statistically don’t exist and you don’t need to worry about them. If group membership should affect reliability, then you need to model group membership explicitly. Remember that reliability applies only to one sample of raters, drawn from a population of raters, rating a single set of subjects. If that’s not what you’re trying to determine, you don’t have a reliability question (at least, not solely).
Thanks for your answer Dr Landers
The thing is, the 3 groups of raters are different (G1= unions, G2=NGOs, G3= media). The 3 groups are assessing the same sample (20 units). I’d like to know if there is ICC within groups. That is, if the raters in the union group have a similar assessment, that there is convergence among the interviewees. In that way I can treat unions (individual assessments) as a single group with the same opinion about the topic/subject.
The same for group 2 and 3.
It’s certainly fine to assess ICC within groups, since that will tell you the reliability of the group mean. But you asked, “How can I provide a general assessment for the whole set?” If you expect the three groups to differ, your RQ is not a reliability question and you will need some other statistical approach. If you don’t expect the three groups to differ, then you can treat them as 14 independent sources of information. It’s one or the other.
Hi Dr. Landers,
Thank you a million times over for a) this article, and b) allowing questions/providing answers! I’m well and truly stuck, and wondering if you might be able to help.
I have hundreds of transcripts of participant dialogue, and 16 different ‘metrics’ (variables, I suppose) that we code the transcripts for. Each transcript therefore gets a count value of each metric, e.g. the participant used 6 of x-type-word, and 14 of y-type-word, etc. I have quite a few coders processing the transcripts, so only have a sample of ten transcripts that have been coded twice, by different couples of coders. My task is to assess how reliably the coders are coding. I cannot seem to get my head around whether I’m able to use ICC (the metrics are categorical, but data is discrete, given its a count, I think?) or should opt for Fleiss Kappa? If needed, I could have three coders code each of the sample transcripts… would that change things for the better?
Thanks in advance,
Hayley
The easiest way to worry about scale of measurement in this case is to determine if your scale is “essentially” normally distributed. Just make a histogram. If it is vaguely bell-shaped, you can probably use ICC; if not, you can’t.
More coders always increases reliability, assuming the coders are equally accurate when coding. What calculating ICC will allow you to do though is project how many people you’d need to achieve a target level of reliability – that is the question you seem to actually want to answer – do I need the mean of 1, 2 or 3 people’s ratings of each of these to get a usable number?
One other concern though is that N=10 is not very stable. Your estimate, whether ICC or kappa, could be highly inaccurate. I would want at least N=30, personally.
Hi
I can’t figure out if I should use ICC or pearson/spearman’s rho to compare the score of observer and patients.
Patients and observer scored the cosmetic outcome of the patients scar after melanoma excision on a scale from 1 (best possible outcome) to 10 (worst possible outcome). I would like to see if the patient and observer score the same scar the same. Other studies using the same survey (POSAS “patient and observer scar assessment scale”) have used different methods, some ICC and others spearman’s.
Sorry for my bad english.
ICC(2,k) for consistency is identical to a Pearson’s r when k=2. So they are the same thing in that particular case.
As to what you can use, it depends on what you are willing to assume about that scale. If you believe that scale is ordinal but not interval, you could not use ICC or Pearson’s r. If you believe it is interval or essentially interval, you can use either.
One advantage to ICC over r is that you can specify agreement instead of consistency, and you can consider more than 2 sources of information. For example, if your patients consistently answered 2 where your observers answered 3 – but it was 100% consistent – would you consider that reliable? If not, you want an agreement-based metric, so neither Pearson’s nor rho would be appropriate – nor would a consistency ICC. You’d need an agreement ICC specifically if you thought you had interval measurement, and if you didn’t, you’d need a kappa (probably weighted).
Thanks Dr. Landers!
Cheers
Hi Dr. Landers,
I am trying to compute an inter-rater reliability measure for 3 raters. For my thesis, raters were required to decide whether a response is present or absent (so yes or no) for brain waves in 47 participants. They were also required to rate how confident they were on a 5-point Likert scale (1 = very poor, 5 = excellent) as well as how replicable the waves are (1 = very poor, 5 = excellent). For example, when a response is very clear, the rater would say response = yes, confidence = 5, replicability = 5. (but raters will likely differ on confidence and replicability when the responses aren’t as clear).
I believe I can use an ICC for the response present or absent agreement between raters…unless there was a better method to use…
but I am stuck with computing how well raters agree on confidence and replicability as it is ordinal. I have tried to research multiple-rater agreement and found modified k statistic like Light’s kappa and Fleiss kappa…
Do you have any advice on how one might compute this type of scenario?
Kindest regards,
Rebecca
You likely want Krippendorff’s alpha in this situation. If you only had two raters, you could use a weighted version of Cohen’s kappa, but with 3 raters, you need Fleiss’ kappa, yet there is no generally accepted way of weighting it. So you need something more general. (Disclaimer: I am not familiar with Light’s kappa.)
Good day Sir!
I am currently doing a research right now and I am having a hard time to what formula should I use for inter rater reliability for 3 observers using an interval data.
At first , I saw Krippendorff’s alpha and thought that it would be good. But upon thinking of the possible things like I need to find a statistician that will compute for me using the said formula which will cost me big.
So now I am thinking what should I do now? Hoping for a response.
Thank you,
Shiela
If you have SPSS, I would suggest you read the article above and follow its instructions to answer your question. If you need Krippendorff’s alpha anyway, you can calculate it in R using kripp.alpha() in the irr package.
Hi sir!
I was thinking that if Krippendorff’s alpha is complicated to compute or use, I will just trim my observers into two so that I can find an easier (if there is such) formula to use. Is that possible? Im not good with numbers actually 🙁
Thank you for the response
You theoretically could do that, but it would be bad science. So I wouldn’t recommend that. If you aren’t comfortable with statistics, you should probably find a statistical consultant for your project. There are many ways to do such things incorrectly.
Dear Dr. Landers,
Thank you very much for your website and blog. This is very useful. I have a question for you if you have time. We are doing an observational study on children’s friendships. One of our variables is observed closeness between friends (rated 0-5). The same and only two coders are coding the 200 dyads of friends on this variable. In the end, we will use the average ratings of closeness provided by the two raters in analyses. Thus, my understanding then is that we should use two-way mixed, average measure in this context: ICC (3,K). We do care about absolute agreement (not only consistency). In our field we aim for ICCs between .70-.80.
1- Am I right that “two-way mixed, average measure” is the good method in this context?
2- If I have the following data (please see below), the ICC (3,k) = 0.00. I see that on 4 occasions out of 5, there was a disagreement between the 2 coders so I guess this is why the ICC is very, very poor (couldn’t be worst at 0.00). Still, on a 5-pt scaling, wouldn’t this only 1-pt difference not that bad given that, in the end, we will take the average rating to correct for such small differences between coders? I guess that because we care about “absolute agreement”, we do need more “absolute agreement” between raters’ scores to increase our ICC and that being “close” (i.e, 1-pt difference) is not sufficient at all? The simple implication would be to have our coders recode these 5 dyads for instance until they are more reliable than this, I guess. Thanks for any comment.
3 2
3 4
2 3
2 3
3 3
3- If I would interchange (for fun) the data on the first row (but without changing the values or anything else) like this:
2 3
3 4
2 3
2 3
3 3
then the ICC(3, k)=0.43. How could we explain this? Is it because ICC(3,k) calculations does not only take into account the correlation between each pair of observation (on each line) but also considers the direction of differences between scores in different columns (e.g., if coder 1 is always lower than coder 2, then ICC is better than if differences between coders are more randomly distributed?
Seb
1. Only if your two particular coders are the only coders that could possibly do this task, i.e., if your only hope is to generalize to those two people. If you believe those coders are a random sample of possible coders (i.e., you could have trained any random two qualified people to do this), then you probably want ICC(2,k).
2. That is occurring because there is too little variance in either coder’s scores to get a stable estimate. You need normally distributed ratings from both raters for ICC to be accurate (i.e., all of ANOVA’s assumptions must hold, since ICC is an effect size calculated from an ANOVA). When there is very little variance, even small differences are magnified in analysis. When done in terms of absolute agreement, the effect of too little variance on estimate stability is even larger.
Thanks for this post, Dr. Landers. Very helpful. Can I bounce something off of you?
I have multi-rater data in which 3 or more raters rated each subject on their EQ. Raters were chosen by the target subject and are different across subjects. I am trying to determine the interrater reliability to help validate the assessment. I was thinking of using ICC. The ICC would be a one-way random model, is that right? And if I am using the average of the ratings in further analyses, I would use the “average measures”? If this is correct, what kind of criteria would I use to evaluate the results? Am I looking for a number 0.70 or above?
Is there a better way to calculate interrater reliability? Maybe using Rwg?
Thanks again!
Yes and yes. The standard is up to you. .7 is pretty typical, but higher is always better for the reasons I explain above.
Thank you! And one more question regarding the analysis above- if I have 3 or more raters per subject, do I need to analyze just the first 3 raters for each subject or can I put all of the raters into the “items” box for analysis?
If you want to do it with the SPSS function, you’d need to have 3 and only 3 raters for every case. Otherwise you’ll get an error. However, the correct way to do this would be to calculate the ICC by hand – then you can use any number of raters per case and calculate the specific reliability estimate you need. Failing that, you could also use a program like HLM to get the ICC. But SPSS won’t calculate ICC if the number of raters differs by case for some reason.
Thanks so much. Would Rwg also be an appropriate analysis to conduct for this research question? If so, can you explain the difference between ICC and Rwg and where I can get more information on calculating Rwg?
Maybe! I don’t know as much about rwg, but I’d suggest you start here: http://psycnet.apa.org/psycinfo/2000-16936-008
Dear Dr. Landers,
I did a study to measure the intra-session and inter session reliability of pain assessment.
I am going to check the ICC for intra-session and inter-session reliability of pain levels reported by participants. My doubt is, should that F test always be significant when we reporting the ICC? or is it enough to have the ICC in the range of reliable with non-significant F test?
If it is not statistically significant, you don’t have a sufficient sample size to support the ICC you found. Or more specifically, you still could have found the ICC you found even if the population level of reliability was zero. Whether that is important or not for your particular study is up to you. I would say that the larger problem is that a large but not statistically significant ICC suggests a huge confidence interval, i.e., very little precision of measurement.
Dear Dr. Landers,
Thanks for the details.
When I checked the ICC, in some instances the ICC is 0.550 and the p value is not significant.
What does that mean? Does it mean the little precision of the measurement?
Should I report both CI and p value related to ICC?
Yes, that is an extremely high degree of imprecision. ICC = .55 that is not statistically significant implies your confidence interval is [0, 1]. That suggests your reliability could be a random draw from any population, i.e., your ICC is random and not a meaningful estimate of any population value.
I would not trust any effect estimate calculated based on a scale with those reliability statistics. If you want to report this ICC anyway, you would probably include both CI and p-value. But in most fields, this ICC and any statistical comparisons you are doing on whatever this ICC is being calculated for would probably not be publishable. I would recommend you collect more data.
Dear Dr. Lander,
Thank you so much.
In this study, I am the only rater who assessed the participants.
Participants attended two days. First day, I took the baseline pain ratings and asked them to rest for 20 min and following rest, same measurement was taken. These two ratings were used to calculate the intra-session reliability.
The measurement took on day two and baseline measurement were used to compute inter-session reliability.
I used Two-way mixed method with absolute agreement when calculating ICC.
Is the selection of calculation method correct?
It might or might not be. You need to clearly conceptualize your rater population to answer that question. The only thing I can say for sure is that the ICC you’ve calculated should generalize to you, and that’s still assuming that the two days you took measures were a random sample of all possible days to which you might want to generalize.
Hi,
I am trying to determine the correct statistic to use in the following situation:
I have categorical data rated by 3 raters. 2 of the 3 raters have rated each of the subjects, but none of the subjects is rated by all 3 raters (so the design is not fully crossed).
Since it’s categorical data, I think ICCs are not appropriate, but it also seems that since it is not fully crossed, Kappa is not appropriate.
Thank you for any help you can offer!
-Shari
That is correct. You probably want Krippendorff’s alpha.
Hello Dr. Landers,
Firstly I would like to thank you for this well-written and informative article.
However I do have a question concerning a study I’m doing. I’ll try to be as clear as possible:
I’m studying if a new technique to diagnose a knee-problem works. So,
a) The same doctor is examining all the patients and he can conclude after the use of the new technique that:
1- the patient has a knee problem
0- the patient doesn’t have any knee problem
After this, a radiography is done to every patient and the radiography gives the right answer: 1- the patient really had a knee problem
0- the patient didn’t have a knee problem
I want to study the reliability of this new technique, but I’m not sure which test I should use.
Should I use another test if the examination is made by different doctors?
Thank you in advance for your help!
Adrián
It sounds like radiography is a “gold standard”? If so, you’re not asking a reliability question, at least with that part – you want to know if the doctor’s technique is a valid predictor of the gold standard detection technique. Validity questions are not generally assessed with ICC.
If you also want to know about the reliability of the new procedure itself, you need replication by patient, e.g., for two doctors to use the technique on each patient. Otherwise you cannot calculate the technique’s reliability. You’d want to know if the doctor’s agree or not (i.e., did they both say 1, both say 0, or did one say 1 and the other say 0), which would likely be assessed with Cohen’s kappa.
Sir-
Thanks for the informative post and for answering all of the questions from those of us endeavoring to learn!
I am hoping you can spare a few minutes to help mentor and teach me! My specific situation follows:
I have a population of 10 coders and 500 essays.
I had planned on executing the following:
Randomly assigning coders to each score 50 essays – ensuring 2 coders evaluate each essay (pairings will vary)
Both coders will evaluate each essay on 3 different factors (self-awareness, other focus and willingness to learn)- each factor will be rated on a 1-7 Likert scale.
The scores from each rater will be averaged to create a single score for each of the 3 measures and then those 3 averaged scores will be averaged into one composite measure for each essay (humility – which is defined as the composite of the three aforementioned sub factors).
Based on what I read, I THINK I need to run ICC 1.
Is this correct?
Now (perhaps) the better question –
Based on your experience, is there a better/more efficient way to assign/execute the coding I outlined?
Thank you again for your time and assistance. I truly appreciate it.
-Jordon
Sounds fine to me!
There isn’t one “better” way to do this coding – there are always trade-offs. The one “best” way to do it would be to have all 10 coders rate all 500 essays so that a) you can calculate ICC(2), which allows you to partial out coder effects and better isolate the effect you’re interested in and b) that gives you a lot of replication such that your ICC(2,10) will likely be quite high. The downside is that you’d be collecting 5000 ratings, and your raters may not appreciate that workload. 🙂
So if you aren’t able to assign all raters to all rating targets, the next best approach is what you describe – assigning a random selection of coders a random subset of rating targets. You might also consider analyzing your data after partially collected to see if 2 raters will be enough to get a stable ICC(1,2) – you might end up needing three or four coders to get an ICC(1,k) at the level you need it to be for further analysis.
Apologies – I submitted too soon.
I would use the “absolute agreement” option.
I would have to run this for each of the 3 sub-factor pairs before averaging them, right? So I’d be reporting ICC results for 3 different variables?
Dear Dr. Landers,
thank you so much for this helpful and informative post. I think I could manage to do the right ICC calculation on my data now.
I have two questions left.
1. Is the relationship underlying the calculation of ICC a linear one like it is the case for the Pearson correlation?
2. What is the difference for the ICC descibed here and the ICC that is calculated in the scope of mutlilevel models? For the latter ICC is for example calculated to check if multilevel analysis is even necessary. In your example (and my data as well) the individual would be the cluster in which multiple observations are grouped. ICC is described as the ratio of the between-cluster variance to the total variance and tells you the proportion of the total variance in Y that is accounted for by the clustering. So I am a little bit confused since this seems to me to be same as ICC used for calculating inter-raterreliability.
I would be very thankful for your help!
1. No. ICC is based on ANOVA, i.e., ratios of within-rater and between-rater variance.
2. The ICC(1) outputted by multilevel modeling is usually ICC(1,1) and ICC(2) is usually ICC(1,k). If it just says “ICC”, it’s usually (but not always) ICC(1,k) – that sounds like the ICC you are describing.
Thank you very much for you help!
I will try to get deeper into the topic, so that I hopefully will be able to differentiate all the different subtypes of ICC.
Thanks again for your quick assistance!
Dear Dr. Landers,
You explained that ICCs are used to establish the reliability of ratings of n subjects by a number x of raters. However, from the answers and other sources I read, I wasn’t sure if it s possible to use ICCs when a small number of raters rate items for themselves. Specifically, I have a small number of raters who rate their preference of items on a 10 point likert scale. I want to use these profiles in an experiment, where other people try to guess their ratings. Before that, I want to make sure that the original raters are distinguishable, meaning they differ in their preferences and then I would want to look at each profile and see the rater’s level of consistency. Could I do this with ICC?
Thank you very much,
Gabriela
Maybe? That would be a strange application and would depend on a lot of details you haven’t provided – you’d need to justify the particular calculation strategy by exploring the assumptions behind it carefully, and the extent to which those assumptions affect the interpretation you’re going for. The bigger problem I think you’d face is converting the ICC into actionable information, i.e., what do specific values imply about your rater sample?
Traditionally, you would do this using a stimulus development study instead, i.e., consulting expert raters, evaluating mean differences, measuring anticipated mediators, etc.
Dear Dr. Landers,
I did ICC test for my raters as they give rates for 20 stimulus of images. And I got 93.6% variance in the mean of these raters. I guess the value is quite high and shows a strong agreement between raters. However, my examiner wants me to find the agreement between those 20 stimulus (images that are categorized into classical and expressive). What test should i conduct to find agreement between stimulus?
I’m not quite sure what you’re asking, but it sounds like you have 10 classical stimuli and 10 expressive stimuli, each rated by at least 2 raters. If your goal is to determine the extent to which the 10 classical stimuli hung together and the 10 express stimuli hung together, it sounds like you might want a coefficient alpha. But I don’t really know from what you’ve posted here; perhaps you should consult a local statistician?
Hi Dr Landers
Thank you for a fantastic post. I have a question regarding the quantification of error in performance outcome measure and most appropriate ICCs to use for this. I am interested in assessing the reliability of a performance outcome measure, a 3 minute walk test in a multi-centre study (multiple raters). I assume that there are 4 potential sources of error in this situation:
a) error of the single rater
b) error between the raters
c) error of the performer, and
d) random error.
To estimate a,c and d I suspect the best study design would be a repeated test
To estimate b, I suspect the best study design would be to have all assessors observe and time the identical video of a single patient.
My ultimate goal is to quantify the ICCs of a-d and as close as possible the”real” score of the patient.
I would immensely appreciate your thoughts on approaching this problem.
Although you could do some of these with ICC, I don’t think that’s an ideal approach. Generalizability theory provides an entire framework designed to partition variance into its component parts in the way you’re describing; I suggest starting with this overview, taking a look at this discussion of g-theory in SPSS, and perhaps this paper for an example applied to an interrater-focused study.
Dear Dr Landers,
I have four methods (i.e., raters), and each method provided estimates for the same 100 targets.
I have computed absolute agreement ICC between each pair of methods using a two-way mixed-effects models.
For a pair of method the ICC = 0.76, with a wide 95% confidence interval (CI) ranging from 0.02-0.91. ICC for the other pairs of methods have way narrower 95% CI.
In terms of interpretation, I was expecting greater scatter in the differences of pairwise predictions for the pair having the wider 95%CI, but this is not the case.
I was wondering what factors may explain the wider confidence interval ?
Thank you very much for your input.
You have the relationship correct; confidence intervals including those around ICC are in terms of standard errors, so a wider confidence interval means that the standard error of that effect is larger. Standard errors can be larger for only two reasons: larger SD or smaller N. So if you have the same number of raters and rating targets for each, the SD must be larger. You should be able to this for yourself with simple descriptive statistics, split by both rater and method. You should find larger SDs related to the larger CI.
Hello Dr Landers,
I have still not figured out the issue.
It turns out that for the pair of raters having the wide confidence interval of the ICC, the absolute differences are narrowly distributed.
So I am wondering if any of the following could be a possible explanation :
1) Very large number of targets treated as random, with only 2 raters treated as fixed ?
2) Interaction between the large number of targets and only 2 raters ? (I used ‘icc’ function in STATA to compute the ICC… don’t know how to check if there was a an interaction and its magnitude)
Also, is there any diagnostics I should check and that could explain this (e.g., residuals of the anova model ?) ?
Thanks again for your help.
I’m not quite sure what you mean, but if you have “narrowly distributed absolute differences,” you probably have very little variance (i.e., range restriction), and that is the cause of the problem. I would take a look at the variance of each rater. Fixed vs random will only affect standard errors slightly, so that is not likely the issue. You can check for a rater x ratee interaction by calculating the ICC by hand. To do that, you’d just need to follow the instructions given in Shrout & Fleiss (i.e., run an ANOVA using rater number and case number as your IVs, predicting score).
Hi Dr. Landers,
To be more precise, for each pair of raters (I have 4 raters, thus 6 pair of methods) I have produced a scatter plot of pairwise predictions (x axis = value from rater ‘i’, y axis = value from rater ‘j’).
Then for each pair of methods I computed the absolute agreement ICC using a mixed-effect model. All 4 raters are rating the same targets. There is a very large number of targets and there is one rating per target (no repeat).
I am struggling with the fact that for one pair of method the 95%CI of the ICC is very wide (ICC = 0.76, 95%CI = 0.02-0.91). I would have expected that this would be for the pair of methods showing more scatter in the scatterplot. It turns out that it is the opposite, i.e., it is the pair of methods having the points more narrowly distributed around the line of perfect agreement (slope =1, intercept=0) (and this is what I meant by “absolute differences are narrowly distributed”).
It’s hard to say without seeing the plots, but I believe my prior explanation still holds. ICC is based in part on the ratio of within-rater to between-rater variance, so if within-rater variance for a particular rater is larger than for the others, or if between-rater variance within a particular pair is larger than other pairs, or both (if the ratio of between to within decreases), you’d expect decreased ICC. You would need to create all of your scatterplots for all pairs on the same x/y scale, on the same figure, to check this visually – I would expect that pair to create an cluster identifiably different from the others. If that’s not it, I’m not sure what else it could be.
Hi Dr. Landers,
I’m helping with the data analysis for a colleague and have run into an issue with ICC that I’m not sure how to handle. In this experiment we’ve had 3 raters provide numeric measures for 25 independent samples. Normally, I would treat this as a ICC(3,1) model.
However, in this dataset, each rater provided 2 measures for each sample. This now creates a ICC(3,k) model where k=2.
My question lies more in the nuts-and-bolts of SPSS, which I’m using for the data analysis. Do I need to manually average the rater’s samples to accurately calculate the ICC value, or can I put all 6 variables into the model at one time?
I’m not sure I follow your train of thought. The way you describe it in the first paragraph, it sounds like you would want ICC(2,3). If each rater also rates a second time, and you believe that second time to be a replication of the first, you actually have a three level model: time nested within rater nested within observation. You would need to calculate ICC by hand, and I don’t know exactly how you’d do that in SPSS. I would probably use Raudenbush and Bryk’s HLM software, if it were me, which would spit out ICC(2,1) automatically (and which you could scale to ICC(2,k) if you needed it using Spearman-Brown). The number used in your final dataset would then be an average of all 6 values for each case.
Importantly though, this assumes no effect of time. If you have a time effect, you’d need to address that somehow (e.g., by running separate analyses at time 1 and time 2). Or if it’s something more complex than time, you’d need to deal with that instead.
Dear Dr. Landers,
Thank you very much for your clear explanation of the options for reliability. Your article is by far the clearest source for information on reliability I have found. Based on what you have explained I think I can use ICC (1,1). I wonder if you could advise me on this.
I am testing a tool which assesses research publications on their quality through 30 questions, of which some are answered on a likert scale. I’d like to test the reliabiltiy of these likert-scale questions.
The study holds 40 raters in total, 5 different publications will be assessed by these participants. To limit the burden for the raters, each rater can only assess only one publication, which result 8 raters per publication.
Am I correct in assuming that because not all raters rate all the subjects, and I am interested in knowing the reliability of a single rater, I can use the ICC (1,1)?
Thank you very much on your advice.
Yes, that sounds correct. ICC(1,1) would tell you how reliable a single person in the future from the same population of raters that you sampled would most likely be answering that question.
I am not sure what ICC measure I need to use for the following situation.
I have 50 teams. Each team has 3 people in it who I am asking to rate that team’s leader. I am going to average the scores from within each team member to create a composite variable. I need to report how similar the scores are for each of the three people in each team, correct? (i.e. person 1 rates the leader similarly to person 2 and person 3) for each of the 50 teams. I’ve seen similar studies reporting ICC(1) and ICC(2) – I’m not sure why they are reporting 2 different ICC scores. Can you help me understand?
Thank you!
“How similar the scores are” is a more complicated concept than you’d think.
Importantly, ICC(1) is Shrout and Fleiss’ ICC(1,1) and ICC(2) is ICC(1,k). In the MLM context, ICC(1,1) captures the proportion of “true” group-level variance that is reflected by an individual and ICC(1,k) captures the proportion of “true” group-level variance that is reflected by the group mean. Thus ICC(1), in your case really ICC(1,1), represents “to what extent do individual scores within groups represent the population mean of their group?” and ICC(2), in your case really ICC(1,3), represents “to what extent do the group means in my sample represent their associated population means”?
Generally, you want ICC(2) to be high to know if you have “good measurement” or not, whereas ICC(1) will be used a marker of how well individuals represent their groups.
ICC(2) will get bigger with larger groups (because more group members = more stable group means) whereas ICC(1) will become more _accurate_ with larger groups (if only 10% of the group mean is represented by an individual in the population, that will always be true regardless of how many group members you have, _but_ more group members will let you estimate that 10% more precisely).
So the practical version: If ICC(2) is low, you probably don’t have enough team members to estimate the team means accurately. If ICC(1) is low, your team members’ responses don’t represent their team’s mean response well, which might or might not be a problem for your particular research question.
Hi Professor Landers,
I hope you had a great holiday break.
Great article and very easy to follow. I just want to be 100% sure prior to assessing my questionnaires test-retest reliability.
I will be selecting a sample of 20 subjects to pilot test the questionnaire.
All 20 will be answering 39 questions. Some of the questions are likert and others are not.
Would I do a ICC (two-way random, average measures) for inter-rater reliability?
So, in SPSS I’d have the columns listed as ‘test 1 and test 2’ in the rows the subjects. Then add up the questionnaire score and enter it in. Then calculate the correlation coefficient. >0.7 is acceptable.
Thank you for your help it is greatly appreciated.
I’m not sure why you’d use ICC in this situation, since you don’t have raters. You would normally just administer it twice and then calculate a Pearson’s correlation between the two scores. That is sometimes called a coefficient of stability.
As for what an “acceptable” value might be for that correlation, it depends on what you’re going to use it for and what the underlying construct is. I’d think of .7 as a lower limit; you never want lower than that, but you might need higher. I would personally want a coefficient of stability over .9 for psychological traits.
Dear Dr. Landers,
Thank you very much for your explanation of IRR. I have learned a lot from your post. Well, I want to ask a question about assessing IRR. According to what I learned from literatures, ICC is one of the statistics for evaluating IRR for ordinal, internal, and ratio variables. As for ordinal variables, can I use Kendall’s W to evaluate IRR? What’s the differences between ICC and Kendall’s W? For example, I have 70 raters to rate 60 items on a 9-point Likert scale. Can I use both of ICC and Kendall’s W to assess IRR?
Thank you very much for your help!
Aoming
You cannot use ICC if your variables are ordinal. ICC is based upon ANOVA (i.e., means and variances) whereas Kendall’s W is based upon ranks. You can only use ICC on ordinal data if you are willing to treat those data as interval, in which case you will get a lot more information about agreement from ICC (because means and variances provide much more information than ranks). I would recommend checking to see if your 9-point Likert scale is normally distributed across cases within each rater; if it is, your data are probably essentially interval.
Dear Dr. Landers,
I am in need of a measure of inter-rater reliability for two raters on a vocabulary test in which answers were judged to be correct, partially correct, or incorrect. The instrument has 80 items, and it was administered to 200 people. In total, there were approximately 3,000 unique responses on the test. Rather than having the two raters each judge all 3,000 unique responses, I would instead like to establish inter-rater reliability with a sample of the responses and then divide the remaining responses between the two raters. (I do not believe this approach to be problematic, but if you do, I would appreciate your input.) My question is whether there are any rules of thumb regarding the number of responses that both raters should judge for establishing inter-rater reliability (and if you are aware of any citations for this). Currently, both raters have judged a few more than 100 (shared) responses, and the inter-rater reliability index was .75. Thank you.
There are two issues at play here: 1) does a single rater have sufficient reliability for you to trust their ratings alone? and 2) are you estimating that number with sufficient precision? You are more directly asking #2, but I’ll answer #1 too.
1) Be sure you interpret “single measures”, ICC(2,1) in your case, as you estimate of the reliability of one rater. I’m not sure if that .75 refers to 1 or 2 raters. If that’s your average raters value, your single rater would only be 0.6. That might be less than the “acceptable” reliability in your situation or it might not. Increasing the number of test ratings will not increase that number; it will only make it more accurate.
2) This is a matter of confidence interval width, so again, it’s somewhat a matter of your personal comfort level. I would personally want 10%-25% of my final sample to account for potential moderators (e.g., one rater is more or less accurate for a particular type of case), but I don’t have a citation for this. Since the width of the confidence interval is dependent on the standard error of ICC, a trustworthy rating N also depends a bit on a number of other factors that are sample specific. I would say that a minimum, you want to be sure that confidence interval does not include zero. Beyond that is really up to you.
Hi Dr. Landers,
Hoping you can help me determine what type of analysis is appropriate for my data.
This is an imaging study where we are trying to determine the intra- and inter-rater reliability of x-ray, CT, and MRI, respectively. We are not comparing the different imaging modalities to one another. I am able to do the intra-rater analyses without difficulty; however the inter-rater analyses are more challenging for me to wrap my head around.
I have 25 subjects and 3 raters. Each rater assessed each subject twice and made a linear measurement (i.e they made 50 measurements in total). This means for each subject I have 6 measurements and I want to assess how similar the readings are; however, I assume that I need to take into account that rater 1’s two measurements for any subject are likely correlated and more similar than a comparison between rater 1 and rater 2. I do not believe that “time” is a factor as all 50 measurements were batched together (the raters weren’t actually aware they were measuring the studies twice).
Can I treat this as a simple ICC analysis with 50 data points and 3 raters or do I need to take another approach?
You definitely can’t do what you’re describing because it violates the assumption of independence.
Importantly “how similar the readings are” is not precisely a reliability question. You might be interested in mean differences across conditions, for example, which is not captured by ICC. In essence, you have a 3Bx2W design – 3 raters and 2 time points. So you might ask this question within that framework instead.
If you ARE interested in reliability, I assume by asking this question that you will eventually calculate the mean of all 6 measurements for each subject and use that value in some other analysis. If that’s right, you can’t use ICC because ICC won’t handle within-person dependencies. I would actually in that case suggest a generalizability framework, since that would allow you to better partition the various sources of variance you are looking at. This is probably the best approach since “intra-rater analyses” may not be meaningful without looking at inter-rater effects simultaneously – you ignore the possibility of interactions.
Also, if I were a reviewer, I would probably question why you asked each rater to make two ratings in the first place if you weren’t worried about any differences over time.
Hi Dr. Landers.
Thanks you for such an informative site. I read through all the comments but am not sure i found an answer to the question I have. I have 2 groups of raters that are each scoring several videos. I have one novice group and one expert group, and they are each scoring the same set of 2 or 4 videos. There are 8-10 raters in each group. I have calculated ICC (2,1) for each group, but now I want to determine if the novice group’s reliability is similar to the expert rater’s reliability. Both groups have high ICC >0.90, the 95% confidence intervals are slightly different, but for the most part they overlap. Other than saying they seem similar, is their a way to actually calculate if there are group differences. The SEM for each group is also very small. The journal I am writing for is asking for the analysis that compared the 2 group’s ICCs to statistically demonstrate that they are in fact truly similar.
Also, while I did use ICC 2,1 based on reading your article above (these are a group of raters involved in a larger clinical trial, we were interested in consistency, and we were looking at the whole groups ability to rate similarly. We simply separated the larger group into 2 groups expert and novice, based on years of experience to then look at the 2 subgroups in an additional analysis), I recently had someone else suggest I should have instead used one-way random or ICC 1,1.
Any thoughts would be most appreciated-
Thank you
It sounds like you are interested in a statistical test to compare the reliability of two related samples – you have two mean ratings (oi) of each case. That is unfortunately a complicated problem. A general approach to it is given in this citation (it talks about alphas, but reliability is reliability):
Hakstian, A. R., & Whalen, T. E. (1976). A k-sample significance test for independent alpha coefficients. Psychometrika, 41, 219-231.
Since you have related samples, you might find this more useful, although I have not been able to read it myself:
Alsawalmeh, Y. M., & Feldt, L. S. (1999). Testing the equality of two related alpha coefficients adjusted by the spearman-brown formula. Applied Psychological Measurement, 24, 163-172.
The ideal way to ask this as a “reliability” question would be to put it in the framework of generalizability theory, so that you can identify the variance contributions of raters and rater expertise distinctly.
Personally, I would not frame that as a reliability comparison. Reliability just assesses how well people agree with each other, and you have arbitrarily defined two groups from one population. I would probably instead look at years of experience as a moderator of rating accuracy, defined some otherwise validated way (e.g., finding previously judged “expert” raters). The issue is that if rating accuracy does vary by experience, you are essentially modeling a between-subject continuous effect with 20 people (not usually a great idea).
As to your second question, if you have the same raters for every case within each group (which you are really treating as quasi-independent samples), ICC(2) is still potentially fine, but you are making the assumption that any interrater variance within the sample is due to randomness within its own group. In short, ICC “corrects” individual raters against the mean rating within each group, so if the group means are different, they correct on different values. That may or may not be a problem for your RQ. Since you are using consistency instead of absolute differences, it probably doesn’t make a difference anyway. But if you are concerned, ICC(1) makes no such assumption. Your ICCs will be a little lower, but not usually much.
I will also say that your design reminds me of the work on median splits which pretty much universally say median splits are not a good thing: http://psycnet.apa.org/journals/bul/113/1/181/
Since you didn’t find a difference, it doesn’t ultimately matter, but that is something to keep in mind – median splits tend amplify apparent differences unrealistically, making it easier (from the researcher’s point of view) to find statistical significance but by misrepresenting the original form of the data.
Greetings, Dr. Landers,
Thank you so much for your article! It was very helpful. I have some questions, however. (I have tried to parse through the comments for people with the same problem as mine, but I found none–or understood none. My first language is not English, unfortunately).
Right now I am in the middle of doing my thesis. I have 40 indicators to measure organizational competence (in 7 point Likert scale) of a company, and 7 raters. These raters are going to measure the organizational competence in the company’s existing condition and ideal condition, using the same indicators.
So I have two data sets here. First the 7 raters measuring organizational competence in existing condition. Second is the 7 raters measuring organizational competence in ideal condition. Later on, I will determine the gap with Wilcoxon.
I am confused about these things:
1. So to measure ICC, I have to make two database, one for existing condition and the other for the ideal condition. Is this correct?
2. The rows are for raters, the columns are for the scores. Is this correct? So there are 7 rows and 40 columns.
3. With 7 rows and 40 columns and two database, I have two different values for ICC for absolute score. Which one do I use, the existing one or the ideal one? Is it the average or the single measure? I’m assuming it’s the average measure?
4. My single measure and average measure ICC score is very different. The single measure is around 0,3, while the average is around 0,9. What caused this? I saw that my data is consistent from one rater to another. I don’t understand why the reliability of my single rater is very low.
Thank you so much for your time, Dr. Landers!
This not asking a reliability question, and ICC is probably inappropriate in this context. You have a sample of N=7 with 80 measured variables. If your 40 variables all assess the same construct, you should use an internal consistency reliability estimate (such as coefficient alpha) to assess the reliability of your items. It sounds like you have two 40-item scales, i.e., existing competence and ideal competence. So you would have a coefficient alpha for each scale.
If you are looking at score differences with a Wilcoxon rank-sum test, that implies you do not believe your competence scale is interval-level measurement. If so, you would not be able to use coefficient alpha either, since it assumes interval-level measurement.
It sounds like you have a lot of seemingly incorrect design and psychometric challenges; I would strongly recommend you seek a local psychometrician to help you with your project.
Dear Dr. Landers,
Thank you for your helpful article. I have a question about structuring my dataset.
I have 3 raters who rate 81 classrooms with an observation instrument that contains 35 items. I am interested in the ICC(2,3) and the consistency between the raters on a 4-point scale. So I was wondering if it would be correct if I would build a dataset with the 3 raters in the columns and 81 (classrooms) x 35 (items) in the rows? Like this:
Rows:
classroom 1 Item 1
classroom 1Item 2
classroom 1- ..until Item 35
classroom 2 Item 1
classroom 2 Item 2
classroom 2-..until Item 35
classroom 3 Item 1
..until classroom 81
Columns: rater 1 – rater 2 – rater 3
If I would be interested in the ICC on item level, I would need 35 datasets with 81 rows (81 scores on the same item) and 3 raters in the columns?
Thank you in advance for your response!
If you want to know ICC for each item, you are calculating 35 unique ICCs. You can do this in a single file. Your dataset should have 81 rows and 105 columns (35 items x 3 raters), but you can just run ICC on the three-at-a-time that you actually need.
When you do that, it is important to remember that this approach likely capitalizes on chance to a pretty significant degree – even if all of the ICCs shared the same population value, you’d expect quite a lot of variation between 35 samples from that population with N=81. So I would suggest that you should only be doing this if your 35 items reflect 35 unique constructs.
Thank you! Thank you! Thank you! I think I made it about 3 paragraphs into the Shroud & Fleiss article before my eyes began to glaze over (and I wasn’t entirely sure I was understanding it).
I want to test the concordance between raters of a risk assessment instrument. My methodology is that there will be 5 raters and 7 scale items rated on a Likert 6 point scale. I want to utilize Inter Class Correlation test? Is this appropriate or is there another test statistic that can give me levels of agreement.
Sure, why not?
Dear Mr. Landers,
first of all, thank you very much for your interesting article and your comments on all these entries which are helpful, too.
Nevertheless, I have a question regarding my case: in a survey, 217 participants rated on a 0%-100% (=1-11) scale the probability to choose a profile. Participants were all presented with 8 profiles and all of the participants ‘saw’ the same 8 profiles. I would like to test the between-person reliability which I would do with ICC(2), two-way random. As you mentioned earlier, I calculated the mean (so the average answer per person across the 8 profiles) and transformed them into rows, so that I got 217 columns with one row which contains the mean. If I know want to calculate the ICC(2), SPSS tells me that there is only one case (N=1) and therefore the command is stopped.
How can I calculate the ICC(2) properly? Should I calculate it for 217 participants with 8 profile ratings instead of with the mean?
Thank you very much for your support!
You should only calculate a mean score if your ratings are across the same constructs. In your case, your sample size is 8, so you should have 8 rows, one for each rating target.
Thank you very much, Mr. Landers!
I know understood that the different profiles are treated as different items (although they measure the same attributes which vary in different levels).
Dear Dr. Landers,
Thank you very much for this article. It clarified many things. I just wanted to know: so if you have only one target, you can’t use ICC?
In my case, I have an experiment having 5 conditions. Each condition has 10 groups of 3 people. Each participant rates 5 variables specifically about the group (group-level constructs). Each variable has 3 items measured on a likert type scale. An ICC(2) would be for example each individual rating every group, right? However, here they only rate their own group, meaning apparently that they have only one target. And I would like to measure how related their scores are within each group. I suppose not but can I use the ICC? If not, would you have any recommendation as to how to approach this problem?
Thank you very much in advance,
Best,
Liz
That’s accurate only if your final unit of analysis is a single group. It sounds more like you have a sample of 10 groups with unique raters, drawn from a population of potential “group members” for each. In that case, you’d have 10 rows (10 groups), 3 columns (3 raters), and calculate ICC(1,1) or ICC(1,3). You could do this on either the individual items or, more likely given what you’ve described, the mean of the 3 items.
Dear Mr. Landers,
0
down vote
favorite
I try to produce test/retest coefficient for our computer based executive function test using intraclass correlation coefficient. The test is very structured computer based test and it has hundreds of short Go/Nogo trials. The subjects have executed the test twice few weeks apart.
So I have dataframes consisting all single trials(df1) and dataframe (df2) consisting average reaction times per subject (n=20) and error percentages per subject.
Question 1: The fixed model is the right model to use, I suppose?
Question 2: What is the true difference between average and single measures at this kind of situations? Which is more recommendable to use, ICC(3,1) or ICC(3,k)?
I suppose using the use of df2 and ICC is best way to evaluate the reliability of our test. Our could I use Pearson with such a low number of subjects?
Thank you!
1) No, it sounds like random to me. Your “raters” are people taking a test and the specific two times they took the tests are an essentially random draw of all possible times they could have taken the tests.
2) ICC(2,1) will tell you the reliability of your test if only one trial is given. ICC(2,2) will tell you the reliability of the participant’s average score over two testing sessions. So the one you need depends on what you will do with it.
Hello Dr. Landers,
I consulted with you previously when conducting ICC tests in my case studies, and I’ve recently completed a pilot study (N=7), so I thought I would consult again to make sure I’m doing it properly. You are very skilled at the ICC test- I trust your feedback greatly! For helping me, I would like to include you in the Acknowledgments section of the article- let me know if that’s ok.
My study investigated a newer therapy for music performance anxiety (Acceptance & Commitment Therapy), with a small sample of vocal students. Each student rec’d 12 sessions of ACT with me as their therapist. After treatment ended, I had two independent raters listen to 8 recorded therapy sessions (chosen randomly) and rate my adherence to the therapy using a validated checklist of ACT-consistent behaviors. The two raters were chosen specifically because they have experience administering this therapy. Each rater rated the same 8 therapy sessions, and their checklist data generated a total adherence score every time they used it. Thus, there are 8 adherence scores (expressed numerically with 4 decimal places) per rater.
I don’t own SPSS and I can’t do an ICC test on my Excel. So… one way I did the ICC test was with an online ICC calculator, through my alma mater (http://vassarstats.net/icc.html).
Below are my adherence scores, and the ICC value I got through that online calculator. Would you mind confirming if it’s correct?
Rater 1 Rater 2
Session 1 0.2604 0.1875
Session 2 0.3229 0.1979
Session 3 0.25 0.1563
Session 4 0.1875 0.2709
Session 5 0.2083 0.2679
Session 6 0.25 0.1417
Session 7 0.3125 0.2125
Session 9 0.1563 0.1563
ICC (3,2) = -0.2187
Thanks in advance for your help!
Cheers,
Dave
Sorry, this data set should be easier to read:
Rater 1 (adherence data going in order from Session 1 to 8)
0.2604
0.3229
0.25
0.1875
0.2083
0.25
0.3125
0.1563
Rater 2 (same)
0.1875
0.1979
0.1563
0.2709
0.2679
0.1417
0.2125
0.1563
That is not what I get in SPSS, although it is fairly close and still negative (i.e., the scores suggest that the two people are not assessing the same construct). There are a few different ways to calculate an ICC, so that’s not altogether unexpected though. I get -.311 for consistency and -.252 for agreement. You can see the cause of it in the data: between cases 1 and 3, as Rater 1 goes up, Rater 2 goes up. But between cases 3 and 4, as Rater 1 goes down to second lowest score in the dataset, Rater 2 goes up to the highest score in the dataset. That is substantial disagreement.
Hmm… that’s interesting you got a different ICC value. To be honest, I’ve been unable to get the same ICC value whenever I use a different ICC calculator (so I figured I was doing the test wrong). I trust the SPSS output you have over my online calculator though!
The problem is actually with this checklist. When using it in my case studies, I was also unable to generate a good ICC value. The “total adherence score” the checklist yields is simply the number of checked items divided by the number of total items that could be checked off. Such a number is not very meaningful, in my opinion, because it fails to address whether SIMILAR items were checked or not. FOr example, 2 raters can both check off 20 ACT-consistent items in a therapy session, and thereby get the same adherence score. But if they’re not checking off the same items, then how is that a measure of inter-rater agreement??
I will have to ask my raters to subjectively report how adherent I was to the ACT manual, because the adherence scores from the checklist are not interpretable.
Well, you’re just assessing the agreement in overall percentage of adherence. That’s meaningful as precisely that. If you want to know agreement on individual items, which seem to be multidimensional, you don’t want ICC – you want a Cohen’s kappa. Then you can assess agreement for each individual dimension and try to isolate where the ICC disagreement is coming from. But with a sample size this small, there will be a lot of noise for that many items.
I’d thought I needed a Cohen’s kappa test, thanks for confirming that. Thing is, it’ll be difficult to assess agreement on individual items, because there’s no clear way to quantify that (the author of the checklist doesn’t give instruction on conducting an item analysis). I’d have to make up my own analysis, which may not be needed for this study’s sake.. I am hoping the potential journal reviewers will be ok with me including the raters’ subjective report of how adherent I was.
Thanks for the quick help, as always!
Dave
if I do inter-observer variability between 9 observers measuring the aortic peak velocities to the same 10 patients, in the output file, Should I choose the single measure or average measures?
thanks
That depends upon which one you want to know.
Dear dr. Landers
I currently am trying to validate a scoring system. I’ve run a pilot asking 4 people to rate 15 cases and calculate the ICC.
I would like to extend my group and ask 30 raters to rate a total of 120 cases.
Since it is too much work for al 30 raters to rate all 120 cases, I will ask each of them to rate approximately 10 cases.
I’ve read in Health measurement scales a practical guide to their developments and use (by Streiner), that in this case ‘the observer nested within the subject’ is applicable.
In the end I will have different raters scoring different cases. For example: rater 1-3 wil score case 1-10, rater 2-5 will score case 11-20 and so on.
I’ve tried to run a test using fake data in SPSS to see if this would work out. The fake data set contains 30 columns and 60 rows. In every column in only ten rows I’ve entered data, the rest of the spaces do not contain data. However when I try to analyze this using a one way random model the output of SPSS says that there are too few cases for the analysis.
I can’t seem to figure out how this works exactly. I’ve talked to my local methodologist before and he’s told me that using the observer nested within the subject may be used but I can’t seem to figure out how to apply this in SPSS.
Could you help me in solving this problem?
Thank you very much
You should think about your raters as per-case rather than per-rater. If you have 120 cases, you’ll need 240 total ratings for 2-ratings-per-case, which is 8 ratings per person. If you want to ask each to rate ten cases, then you’ll end up with 300 total ratings, which I wouldn’t recommend since it will result in a different number of raters per case, which SPSS can’t handle. Instead, I would target 360 total ratings for 3-ratings per case, which is 12 ratings per rater. In this setup, you would then have three columns for the first, second, and third rater per case, which would be a final dataset of 3 columns and 120 rows with no missing data. Then you will probably want ICC(1,1) to determine the reliability of a single person using your scoring system.
Thank you very much for your reply, I really have been struggling with how to make SPSS work, this solves my problems (and affirms that I was trying to test reliability in a possible way!).
Hi Dr. Landers your post is really a remarkable addition… actually a clear explanation on the subject. But i am in very much need of your help as my data set is different from all above discussed, because i have read almost posts and replies above.
Actually i have 4 variables in my model one I.V, one D.V and two mediators.
IV i.e. HPWS (Have 26 items) and First mediator i.e. (Organizational Commitment having 8 items) are responded by faculty members in my questionnaire part 1.
D.V i.e. (Organization Performance having 5 items) and 2nd mediator (Human Capital having 5 items) are responded by HODs or Faculty members who have some administrative position in the university.
Actually what i wanna clear that i have different respondents for my survey and even unequal because Admin are less than Faculty members in every department.
I have entered my data in spss in items form i.e. each item responses in column that means for HPWS have 26 column responses an so on upto OP Variable.
Now what i wanna ask you that i have to compute ICC1 and ICC2 for my data in SPSS.
I am much confused about it.
Please Help me out on this as soon as possible.
Thank you very much!
Here i wanna mention that i have 682 total responses that includes 545 responses to Part 1 of the questionnaire and rest 137 for Part of the questionnaire.
Thank you.
I would not recommend ICC in this context to assess reliability. It sounds like you just want coefficient alphas based upon the design you have described (basic single-level mediation).
Hello sir,
Actually i have to compute ICC1 and ICC2 for my data reliability because it is required by research supervisor for my Paper.
Here i wanna mention that i have collected data fro a total of 19 universities. and first i have to aggregate my data from individual level to organizational level, and to justify this aggregation i have to compute ICC1 and ICC2.
As i directed my supervisor, i have to first transpose my variables in SPSS then apply ICC then Aggregate data on University or Organization level and then finally i have to test model in PLS-SEM.
But i am stuck in finding ICC.
Need your kind feedback and guidance.
I can share my data file with you if am not communicating the problem clearly?
I have gone through many online lectures on YouTube regarding subject but found your article the only helping tool! and i think i am a little away from solution and hope will done with your expert guidance.
Thank you very much.
Ok, in that case, you are not asking a reliability question. You are asking a multilevel aggregation question. That is an entirely different problem. The ICC(1) you’re referring to corresponds to ICC(1,1) in my description and ICC(2) corresponds to ICC(1,k). If you have different numbers of observations within each organization, you cannot calculate either ICC using the SPSS tools I’ve described here. You’ll need to either 1) run an ANOVA according to the models provided in Shrout & Fleiss and then mathematically derive each ICC from the ANOVA summary table or 2) use a program that will tell you this number automatically, such as HLM or R.
I am planning to write up some specific instructions on how to do this with SPSS and Excel, but it won’t be available for at least a month.
Importantly, aggregation is often not preferable to multilevel modeling keeping group identities intact. If you have any cross-level effects, you won’t be able to test them with an aggregated dataset. If you have poor within-group agreement (i.e., low ICC), you can’t justify aggregation at all. So I would just recommend you be careful with jumping to aggregation as the solution to your problem.
Thank you very much dear Landers, for detailed answer what i understand from it is, i cannot find ICC directly in SPSS because no of responses are unequal. and i should try the other two methods you told.
But here please clear me one thing whether we apply ICC on items or variables? is it depends on nature of variable or study etc?
In my case i am supposed to calculate ICC for variable (Average of items) or for items individually?
I am even confused about raters? Who are raters in my study ? Teachers or university as a whole i think ?
If you are going to be using scale means in further analyses, you should calculate ICC on the scale means. If you are going to be using individual items, you should calculate ICC on individual items.
Conceptually speaking, the “raters” are members of whatever group they belong to. If you are planning to aggregate teachers up to the university level, teachers are raters of their own universities.
hello sir, i am sorry for thanking you late. You really helped me a lot. I will not hesitate to ask if i feel some problem again.
Best regards
Hi Dr. Landers,
I wanted to confirm with you that my data analysis for a new set of data is correct ( I use a program called StatPlus, not SPSS, and I’m not sure I trust my output)…
I recently finished a uncontrolled pilot study investigating a new therapy for music performance anxiety (Acceptance and Commitment Therapy) with a small sample of university vocal students (N=7). One hypothesis was the students’ overall performance quality would improve from pre to post. I tested this by recording each student perform 2x at pre-treatment (once a cappella, once with accompanist) and 2x at post-treatment (same). Each student was asked to perform 4 different pieces that were of similar length and complexity. They were asked to do 4 different pieces, rather than the same piece 4x, in order to minimize the likelihood that a practice effect may occur from pre to post.
3 raters were then hired to independently watch and rate the performance quality of all students’ recorded performances. They were blind to the study’s purpose and to the order of videos (i.e,. they didn’t know which were pre or post). They used a valid scale to rate each student’s overall performance quality, the Music Performance Quality scale, or MPQ. Each performance is graded on a 1-5 scale (1= awful, 5=excellent).
Using data from all 3 raters’ I created two columns in StatPlus – one for pre ratings and one for post. I then ran a simple linear regression with pre ratings = ind variable , and post= dependent variable. The results were the following: Y = 1.12363 + 0.71007X, where Y represents a student’s post-treatment quality and X is pre-treatment quality. The slope is positive and significant (F = 44.73, p < .01). Clearly this shows the slope is positive and significant, which indicates my hypothesis was supported.
Without knowing the actual ratings, would you say I did the data analysis correct in StatPlus?
Also, to calculate effect size, I used a Cohen's d test. I used the mean rating at pre-treatment, the mean rating at post, standard dev at pre, standard dev at post, and the sample size to calculate Cohen's d.
Without knowing the mean, SD, or sample size of ratings, did I correctly calculate effect size for the degree of change in ratings from to post?
Thanks! And I will be including you in my study's acknowledgements section!
Dave Juncos
You’re getting pretty deep into the weeds of your particular method, so it’s a bit hard for me to follow, but I will say that I don’t see how you got from 4 pieces (sounds like 4 measurements) x 2 pre-treatment + 2 post-treatment to that analysis. It sounds like each of your 7 students did 16 pieces. With 3 raters, that’s 336 distinct ratings. However, to run the analysis you’re talking about, you can only have 7 rows for any between-person analysis. That F is huge, so it suggests to me that you probably didn’t do that or that something else is off with your dataset.
There are a few ways you might deal with that problem. One would be to look at each of the 4 pieces separately (pre-post for each). Another would be multilevel modeling (so that you can distinguish within and between person effects). If I’ve misinterpreted your design, this might not apply of course…
Thank you so much for responding! I apologize for getting too into the details of my study. You’re correct, it’s too much to take in.
There were 7 students total, and each gave 4 performances (2 pre and 2 post treatment). However, one student missed 2 performances, so the total number of performances to be rated was 26 (not 28).
What I did to calculate a Cohen’s d was take all 13 ratings from 3 judges at PRE, and compare them to the 13 ratings at POST. In order to do that, I simply needed to know the Mean/SD/sample size for the PRE ratings and POST ratings. Here is that data:
PRE DATA ACROSS 3 RATERS
M = 3.25641
SD = 0.78532
N = 39
POST DATA ACROSS 3 RATERS
M = 3.43590
SD = 0.75376
N = 39
The Cohen’s d is small (0.23) using all 3 raters, but it’s still significant. I believe this is correct.
Ok, I see. They did 4 different pieces, and the order of the pieces were counterbalanced across participants to account for order effects.
In that case, I was still correct about the independence issue – you can’t do that. You are likely getting an attenuated error term for that reason (i.e., this is why your F is so unusually high).
For that sort of design, you can still 2 different things. The most precise is multilevel modeling. The most straightforward to do that would be RM-ANOVA, with a 2 (within-pre/post) x 2 (within-ordering; first or second piece). In this approach, N=7, but you have 4 observations per person. You’d be looking for a main effect of pre/post but the absence of an interaction or main effect of order.
The second option is to use ICC to determine if it would be acceptable to aggregate within person. In that case, you’d want to calculate a set of ICC(1) for the 2 pre scores and another set of ICC(1) for the 2 post scores. If ICC(1,1) is greater than .12 and ICC(1,2) is greater than .6 for both post and pre, you can justify calculating mean scores within pre and post. Then you can run the analyses you described here (regression, d-values, etc). In this approach, N=7, but you have 2 observations per person.
You definitely can’t have people represented on multiple rows and calculate a mean, SD, or any other statistic that relies on means and SDs. It violates the assumption of case independence for that entire family of statistics.
Ugh… I was afraid I did it wrong. OK! Thanks for pointing this out! Man I’m glad we spoke prior to submitting my article for publication!
I am downloading a free trial of SPSS as we speak…
I’d like to do the RM-ANOVA you suggested. I assume the output of that will give me F and p values? But will it give me effect size data too (like Cohen’s d or Hedges’ g)?
I am now entering the data in SPSS. Any guidance on how to set up the rows/columns in my SPSS file?
For the RM-ANOVA approach, you just want to have 7 cases with 4 variables each. You’re going to be quite low power for anything but large effects though. If you still have your rater data (with 3 raters per 4 variables, you’d have 12 ratings per row), you’ll need to calculate rater composites first for each of the 4 values that will actually be used in the ANOVA.
You will get an F and p-value for the entire model, and then assuming you find a significant F, you’ll need to conduct post-hoc tests to determine what combinations are actually significant different from which others. Here’s an overview: https://statistics.laerd.com/spss-tutorials/two-way-repeated-measures-anova-using-spss-statistics.php
N=7 is quite small for this sort of question, so you’re going to be underpowered for anything except quite large effects. Although perhaps you have quite large effects. 🙂
I guess it’s like this for each judge?
Student 1, Student 2, …. Student 7
pre-rating 1 Pre 1 Pre 1
pre-rating 2 Pre 2 Pre 2
post-rating 1 Post 1 Post 1
post-rating 2 Post 2 Post 2
How do I run the ANOVA using all 3 judges’ data?
Ok, thanks!!!!! I will try this on my own now and be in touch if I have further questions…
Ok, in SPSS, I’ve now created 7 cases with 12 variables each, here is what each case looks for each student:
Student
1) Judge 1’s rating for PRE perf #1
2) Judge 1’s rating for PRE perf #2
3) Judge 1’s rating for POST perf #1
4) Judge 1’s rating for POST perf #2
5) Judge 2’s rating for PRE perf# 1
6) Judge 2’s rating for PRE perf #2
7) Judge 2’s rating for POST perf #1
8) Judge 2’s rating for POST perf #2
9) Judge 3’s rating for PRE perf #1
10) Judge 3’s rating for PRE perf #2
11) Judge 3’s rating for POST perf #1
12) Judge 3’s rating for POST perf #2
However, when I come upon the “Repeated Measures Dialogue Box” I have 7 cases in the left hand box, but I am only able to transfer 4 into the “Within Subjects Variables box (pre/post, order)” on the right.
I don’t know how to get all 7 from the left into the right, so all my data gets entered into the RM-ANOVA analysis!
How can I proceed?
You’ve already justified aggregation by judge with ICC, yes? If so, use the Compute Variable function in the Transform menu to create means for each variable. Info here: http://libguides.library.kent.edu/SPSS/ComputeVariables . You’ll want, for example, to create a new variables equal to something like: MEAN(pre1_judge1, pre1_judge2, pre1_judge3). Do that 4 times to create your four variables representing mean judge ratings. Use that in RMANOVA as that previous link I sent explains.
If you’re interested, can I send you the raters’ data ?
I don’t know how to do the ICC for aggregating within person…
Do you do stats consulting work? If so, I’d like to hire you to help me run these tests. My email is dimazzadj@yahoo.com
Thanks so much!
Dave Juncos
Hi Richard
I am currently doing my dissertation and am really struggling with the statistical element , as I have no background in it. I have 17 raters rating an outcome measure which consists of 10 components and I want to generate ICC scores for the measure both as a whole and for each individual component. I think i’m going wrong when I go to analyse the data by selecting the wrong parameters, I currently have all 17 raters over the right side, with the single column on the left side representing the 10 components of the measure. I then select Descriptive=Items, Inter item as correlations, Summaries as means and variances, tick ICC,Model as 2 way mixed and type as absolute agreement. The results seem to be inaccurate and comparing the wrong things , it appears its comparing each rater to their own scores, rather than compare all of their scores for each component.
Any help would be greatly appreciated
Regards,Alex
Yes, sounds like it. It might be easier for you to conceptualize raters as if they were items on a scale – each rater should be its own variable. If you want to know reliability for multiple components, you’ll need to have separate ratings of each component (i.e., separate variables).
Hi Dr Landers,
Fantastic article explanation, really helped improve my understanding. I have done data collection using the same machine (providing clinical, continuous data) on 14 subjects. Each subject has repeated the test a total of 10 times.
I want to assess both the repeatability and reliability of the machine in providing the results. Am I correct in saying that I should use a repeated measures ANOVA for repeatability and ICC for reliability? If so, what model of ICC should I be using? Given that there is only one rater and is more of an assessment of intra-rater reliability.
Thanks
Repeatability is a way to conceptualize reliability, so those are the same thing, and ICC is just a mathematical transformation of various types of ANOVA. So I would recommend you look at both simultaneously with ICC and then calculate all the various ICCs you want. Alternatively, you could use a generalizability theory framework which would allow you to partition the variance by source, which would give you a better sense of what specifically is contributing to what. I would also probably recommend against ANOVA if you expect any linear effects over time, which I suspect you do, or otherwise you probably wouldn’t have re-tested them 10 times.
Dear Dr. Landers,
Thank you for the helpful summary. I have a question regarding the appropriate test for my specific study design. I have asked 6 clinicians to rate 6 images on the absence or presence of 2 bacteria (S and P) twice. Possible answers were:
0. nothing present
1: only S present
2: only P present
3: both present
We now wanted to calculate the interrater reliability and were wondering:
1: If an ICC would be a good test for this (considering that my variables are categorical rather than numerical)?
2: How we should we code our variables? I have now used a wide format with the raters in rows and picture 1 – 6 in columns. With variables being 0, 1, 2 or 3. Would it also be possible (or even favourable) to code them as correct or incorrect?
3: What model we should use? Reading the original article, I would think two-way random. What is the difference between the two ‘types’? (consistency or absolute agreement)
No, you can only use ICC with interval or scale level data. You could transform the ratings into two dichotomous variables (i.e., var 1: S present (1) or not present (0); var 2: P present (1) or not present (0)), but you lose some information in doing so. I would recommend instead looking into Fleiss’ kappa which will handle categorical data or Krippendorff’s alpha, which is a generalized version of basically all common reliability statistics.
Hi,
I am examining inter-rater reliability of performance in my task and the degree of similarity of ratings collected from 6 different judges. This work will determine the dependent variables that will be used to operationalise the construct of trainee performance.
Can you please advise me on what to do.
Thanks,
Monica
I would recommend reading the article you are commenting on, which gives you step by step instructions for this situation. Although I will say that reliability analysis alone should never determine operationalization.
Hi Dr. Landers,
Thank you for this helpful summary on ICC.
I need to analyse the inter-rater and intra-rater reliability for a study where 2 raters (sample) have carried out measurements (2 each) on a flow model at 9 different settings giving 18 measurements for each rater.
1) Am I correct in analyzing inter-rater reliability using a two-way random model (selecting absolute agreement)
2) In the SPSS output, do I take the result of the average measures for the entire set of measurements or do I have to separately assess each of the 9 settings?
3) How do I assess intra-rater reliability?
4) Do I report the output as [ICC(2,2)=***] and quite the Fleiss paper?
Thank you for your help on this.
1) Sounds reasonable.
2) It depends on if you consider your 9 settings a random distribution of settings, i.e., randomly sampled from some generalized version of a setting. If so, you can calculate a mean score among settings and then calculate ICC on that.
3) Same basic idea, transposed dataset – time is your rater, in that case.
4) That is reasonable. You can also cite the journal version of this website (cite above).
very very good!
Thank you so much!
I will check out your book since your posting here is so easy to follow!
Thanks! Although to be clear, the book is a first-year introduction to statistics, broadly. I actually am working on a graduate-level research methods text too with a coauthor, but it’s still about a year away.
Hi Dr Landers,
I reviewed posts of your ICC related issues. They are very useful, however, too many till I am not sure. I would like to ask whether my decision about ICC is correct or not. I examined test-retest reliability of self report questionnaire consisting of many domains. Each domain have many items. Each participants (40 persons) did the questionnaire 2 times (2 weeks apart). I decided to use ICC 3, k because many items in each domain were averaged. However someone said it should be ICC 3,1 What will be your suggestion?
It sounds like you have a sample of people and not a population, so that would actually be ICC(2).
If you want ICC(2,1) or ICC(2,2) depends on what you want to do with it later. If you want to show that the questionnaire would be reliable if only administered once, you want ICC(2,1).
Thank you very much for your suggestion! By the way, referring to McGraw and Wong 1996. “Forming inferences about some intraclass correlation coefficients” in page 33 informed about average measurement including the average rating for k judges, average score for a k-item test, or average of k litter-mates. Even though it seems to measure once per session, within the questionnaire, each domain , say part of perception in friends and family, ratings of items in this domain were averaged before analyzing data. This can be viewed as measuring the same issue for multiple times or not.
Dear Dr. Landers,
I’ve read your interesting and exhaustive article, but I am unsure about how I should deal with the calculations of ICCs in my case. I’ve recruited a total of 36 lay users who independently evaluated six mobile apps (6 raters per app), using an instrument (Mobile App Rating Scale). The instrument is composed of 20 items (measured through 5-point Likert-type scales), grouped within 4 domains. So, to summarize, the unit of analysis is a mobile app, rated by 6 people according to a set of items.
The literature using the same instrument reports two-way random ICCs with absolute agreement (average scores).
My main question is about the format of the dataset – as it is now, I have the participants (raters) as cases, and the items (ratings) as variables. This way I can evaluate the internal consistency of the tool (within each domain), but I am not sure the ICCs calculation is correct. I would appreciate your advice about this situation.
Thank you in advance!
Best wishes,
Marco
Whatever you have as columns is what you are assessing the consistency of. So if you have 20 items in 20 columns, you’re assessing the consistency of the 20 items with each other. In this case, ICC(2,k) is equivalent to coefficient alpha. If you put 6 people’s ratings in 6 columns, you’re assessing the consistency of whatever they were all rating. If the “unit of analysis is a mobile app” I would think you should have 1 mobile app per row, and 1 rating of each app per column. If the 20 items are the same, you’d probably want to calculate coefficient alpha on your items first (to establish scale reliability) and then use mean scores as your new columns for ICC (to establish rater reliability). Thus I’d guess you’d want 6 rows and 24 columns (6 ratings per 4 domains).
Having said all that, you probably actually want generalizability theory, since that would allow you to partition rater-contributed, app-contributed, and scale-contributed variance. As is, you will need to make a lot of assumptions.
Dear Dr. Landers,
Thank you, that’s helpful. I will take a closer look at the generalisability theory literature as I am not familiar with it.
Let me clarify again a few points: 1) According to the Mobile App Rating Scale scoring protocol, 5 sub-domain scores (engagement, functionality, aesthetics, information, and subjective quality) are computed by averaging the items in each of the four sub-domains. 2) Then a total score is calculated as average of the first four sub-domains. I have then 6 outcomes of interest.
I calculated Chronbach’s alpha for the items in each outcome, for the overall sample of raters (n=36) and for each app (raters=6), as each group of raters evaluated only one assigned mobile app. This way I could determine whether the instrument was consistent or not and whether the items were overall measuring the expected “constructs”. The developers of the Mobile App Rating Scale do not provide any recommendation regarding internal consistency, in case alphas are poor or unacceptable.
As a matter of fact, I found some “problematic items” in some sub-domains and I will discuss this finding, as I have some ideas about the reasons for inconsistencies.
Now, I am also interested in determining the level of agreement among the raters for each different app, so that I can conclude whether their ratings could be “trusted” or not.
If I understood you correctly, I could then calculate the inter-rater reliability using ICC let’s say for App#1 (evaluated by raters A, B, C, D, E, F) to conclude whether “six people independently rated the application in a consistent way” (so they agreed with each other in a satisfactorily way > satisfactorily = based on thresholds for ICCs)
The dataset look as follows:
A B C D E F
2.8 3.2 2.2 3.2 4.5 4.4
4.3 3.5 4.5 4.7 4.3 5.0
3.3 – 4.0 3.7 4.7 5.0
3.8 4.0 4.5 4.3 4.8 4.0
3.5 3.6 3.8 3.9 4.5 4.6
1.5 2.5 1.5 3.8 4.3 4.8
Note: there is one missing data point.
The syntax I used is:
RELIABILITY
/VARIABLES=A B C D E F
/SCALE(‘ALL VARIABLES’) ALL
/MODEL=ALPHA
/STATISTICS=DESCRIPTIVE SCALE CORR
/SUMMARY=TOTAL MEANS VARIANCE
/ICC=MODEL(RANDOM) TYPE(ABSOLUTE) CIN=95 TESTVAL=0.
An ICC model with two-way random effects, using absolute agreement definition gives me:
ICC single measures (95% CI) = .341 (.129 – .881)
ICC average measures = .949 (.842 – .996)
How would you then report the results? Can I say that “on average, the raters of App#1 showed good to excellent inter-rater agreement”?
Another question is related to the way SPSS deals with missing data: when I use the command /MISSING=INCLUDE the results of the same above calculations change as follows:
ICC single measures (95% CI) = .270 (.034 – .796)
ICC average measures = .690 (.176 – .959)
Thanks a lot again for your advice!
You’re getting into some very project-specific types of questions, but I don’t understand why you would only look at one app at a time. The construct needs to be consistent for all values – that is the whole point of reliability – so you should be calculating one ICC for engagement, one for functionality, etc.
All the /MISSING=INCLUDE command does is instruct SPSS to ignore missing value specifications. What that means is, for example, if you left that missing value blank in your dataset, it would analyze it as a zero. I would not recommend ever using /MISSING=INCLUDE for any analysis because that functionality is not something you should ever need.
If you want to avoid listwise deletion, you’d need to calculate the ICC by hand, by running the ANOVA model described by Shrout & Fleiss, and then calculating the ICC by hand. SPSS is not designed to handle missing values in ICC calculations since it is designed around survey analysis, which is a context where you would generally not want missing data to inform how you develop your scale items. But for inter-rater analyses, or specifically ICC(1) and ICC(2), that’s not true, since there’s nothing unique about each rater.
Thank you for your response. Sorry, I am trying to be more specific because I still did not understand if I am doing mistakes because of the way the dataset is organized.
Now, is the following format what you suggested?
A_item1.1 B_item1 .1 C_item1.1 D_item1.1 E_item1.1 F_item1.1
App1 2.8 3.2 2.2 3.2 4.5 4.4
App2 2.8 3.2 2.2 3.2 4.5 4.4
App3 2.8 3.2 2.2 3.2 4.5 4.4
App4 2.8 3.2 2.2 3.2 4.5 4.4
App5 2.8 3.2 2.2 3.2 4.5 4.4
App6 2.8 3.2 2.2 3.2 4.5 4.4
(I just copy-pasted for convenience, but the data differ, of course)
The problem of this format is that it assumes that the same raters and apps are not the same (but I have a group of 7 raters and 5 raters for two different apps).
The data I have is the following:
App1 App2 …. App3
A B C D E F G H I L M N O P Q R S T
Item1 (of domain 1) 2.8 3.2 2.2 3.2 4.5 4.4 …
Item2 (of domain 1) 4.3 3.5 4.5 4.7 4.3 5.0
Item3 (of domain 1) 3.3 – 4.0 3.7 4.7 5.0
Item4 (of domain 1) 3.8 4.0 4.5 4.3 4.8 4.0
Item5 (of domain 1) 3.5 3.6 3.8 3.9 4.5 4.6
Item6 (of domain 1) 1.5 2.5 1.5 3.8 4.3 4.8
A-F are the raters of App1 and Items1-6 are the targets.
Another group of 7 raters G-O has evaluated App2, using the same targets, and a third group of 5 raters (P-T) has evaluated App3.
Does this clarify my problem?
So, this is why I would look at different apps separately, because the groups of raters are independent – as they haven’t evaluated the other apps.
I think this may be getting too in the weeds for me to provide advice via blog comments. I will try one last time though.
Reliability refers to the percentage of true score variance in a variable is captured by different, independent measurements of it. This is what ICC does. It assesses a measure’s reliability in assessing a construct. Your app is not a construct. The dimensions of your instrument are. So the only valid way to use ICC in this context is to assess the consistency of your instrument.
You cannot assess reliability of your apps because you have no replication by dimension by app. You would need at least 2 ratings on each dimension within each app to do that. Therefore you have no way to estimate reliability for rating an app. You would need to collect more data to do this.
Conceptually, it is also not valid to use items as cases within an app because the items are not random samples of items from the same domain. This violates several assumptions of reliability assessment in general.
Having said all of that, you could look at items within a scale as items within an app, i.e., capturing to what degree engagement is assessed by the various items used to assess it within app1. But that is really just a coefficient alpha split by app, which I believe you’ve already done.
Dear Dr. Landers,
Thank you again very much for the response. I think I will stick to the internal consistency of the scales and will not delve into ICCs as this is not appropriate.
I still have one more general question for you: how could you determine the level of agreement among 6 judges who independently scored an object using a set of scales?
Still the same. Inter item inconsistency can be assessed with a consistency icc(2,k) aka coefficient alpha, and inter rater agreement of scale means with an agreement icc(2,k). If you want to look at them simultaneously, you’d need to partition variance explicitly, with an approach like g-theory.
Dear Dr Landers,
May i know, why i got icc score zero eventhough the agreement between both rater seems to be good. Both raters rate the same score to almost all the subjects (n=123) ?
Thank you
ICC assumes normally distributed data being contributed by each rater. If your data are non-normal, many strange things can happen because ICC assumptions are violated. In such cases, you should use an agreement statistics that does not require normality, such as Cohen’s kappa.
Dear Dr. Landers.
Thank you for this wonderful resource.
I am looking at a 10-item teacher rating scale. 50 students were each rated by 2 different teachers; however, the pairs of teachers were not the same for each student (i.e. there were a total of 7 teachers, different pairs rated different students.) I am looking to calculate interrater agreement for the scale using mean scores. Would I need ICC because the raters are not the same? Could I use Pearson correlations instead?
Thank you!
A Pearson’s correlation will only assess consistency, not agreement, so no. Additionally, Pearson’s assumes your pairs are meaningful (numbers in column 1 are linearly related to column 2), whereas in your case the labeling of “teacher 1” vs “teacher 2” seems arbitrary. ICC does have one critical assumption though here – you need to assume there are no teacher-effects, i.e., that none of your teachers are rating consistently differently from other teachers (e.g., no teacher is consistently harsher or more lenient than any other, regardless of the student being rated). If you are comfortable assuming that, you can use ICC(1). If you aren’t, you need multilevel modeling.
Thank you for the response. Is there any statistical method to test the assumption that there are no teacher effects before doing the ICC?
That is what you’d be able to do with multilevel modeling.
Dear Dr. Landers
That was an excellent article and it has been able to disabuse my mind about calculating the inter-rater reliability. You have so many article online but I want you to know that this one stands out. May the good Lord continue to keep you.
Sir, myself and the team of researchers in my organization just concluded a study, and analyzing the data has become a subject of argument with no end, and that is why I have been given the mandate to comb every available literature and come up with the best approach in analyzing the data from the field study.
The is the data gathering scenario, the study comprised of 5 different areas (A, B, C, D, and E). The thrust of the study is to find out how reliable is the ratings of examiners from these 5 different areas. Same 30 candidate scripts were photocopied and given to 8 examiners from each of the areas to mark and their marks were recorded.
If we want to calculate the inter-rater reliability between two examiners from 2 different areas, what will be the best approach out of the three you have mentioned and how do we go about it; and if we want to calculate for more than 2 examiners, say 3 0r 4 0r 5 0r 8; how do we go about it.
I will appreciate your kind giudiance in this regadrs
Thank you
Bakare, Babajide Mike (Jnr) Ph.D.
I would strongly suggest you look into generalizability theory; you have multiple sources of variance that in any traditional analysis would require making many assumptions. That is likely why you are disagreeing with your colleagues; you disagree on the assumptions that are reasonable. G-theory works well in this context because it allows you to partial out the variance contributed by each source, i.e., area-contributed, examiner-contributed, and script-contributed, in addition to random error and other potential sources.
Dear Dr. Landers,
Thank you for your explanation.
I was wondering if I can also use ICC as a test-retest analysis.
100 parents have filled in a questionnaire about their child, 6 weeks later the same parents filled in the same questionnaire about the same child. I would like to find out if the scores of this questionnaire are stable over time.
Should I use tw0-way-random , single measures, absoluut agreement?
Thanks for your help,
Kind regards,
Esther
Sure. But that sounds to me like one-way random, since your “raters” are not consistent across children (i.e., each child has different parents).
Thanks for this post! I was hoping you might be able to help my specific study which is based on the “think-manager-think-male paradigm (in case you’re already familiar with it).
I distributed a survey including a list of 50 traits to 3 different groups who had to rate them on a scale based on a different question (whether these traits pertain to a woman/man/manager).
I need to use an ICC analysis for assessing the similarity of ratings between the 3 groups – so I can check whether the “man” and “manager” ratings are more similar in comparison to “woman” and “manager”.
After reading your post, I understand that I believe I need ICC(2) based on means and checking only for consistency. But since this between-subject paradigm seems pretty different from most examples, I’m still not quite sure how to go about it.
Also, after I check the similarities between groups – is there a way to check the effect of co-variates like age and gender of rater?
I’m not really seeing how ICC helps you here. ICC is really a tool for estimating inter-group consistency – not for hypothesis testing, which it sounds like is your goal. “If man and manager are more similar than woman and manager” sounds like a hypothesis to me at least. If so, you should really test it that way, e.g., with regression or ANOVA. That may be why you are having a hard time seeing how ICC would be used. Covariates cannot be used here; that is not the purpose of ICC. ICC assumes that all raters are drawn from the same population (or are a population themselves, in the case of ICC(3)).
Hi Dr. Landers, thank you so much for taking the time to respond. After reading more articles on this paradigm, I managed to find one that provided a detailed explanation of how they utilized ICC.
Each trait was averaged among respondents, so each condition acts as a rater. And to examine the effect of the respondent’s gender, they just calculated ICCs only based on the specific gender. So I know now to use two-way random and check absolute agreement.
In any case, thanks again for this post and for your time!
Thanks very much, very useful.
BTW, I noticed that in running the procedure for three raters per target (not always the same over targets), the ICC (average-measure one-way random) result is identical (to two decimal points) to Cronbach’s alpha. What does this mean?
Thanks for your time.
Well, Cronbach’s alpha and ICC(2,k) are actually identical computationally. If ICC(1,k) does not differ from ICC(2,k), it only suggests that controlling for rater effects does not affect the rest of the model.
Hello Dr. Landers,
Thank you so much for your excellent source and kind support.
Earlier on April in reply to Tahir, you told ‘I am planning to write up some specific instructions on how to do this with SPSS and Excel, but it won’t be available for at least a month’.
Is there is any tool ready now?
Best regards,
saeedmohi@gmail.com
Unfortunately haven’t had time! Still on the list!
This is nice and handy. I’ve looked at many sources and tried many packages but have had difficulty with the following scenario: I have lots of targets and lots of raters and each rater rated a random subset of the targets, resulting in a dataset with lots of empty cells. For instance, in one case, there are 115 targets and 1209 raters, and just several ratings per target (with slightly different number of raters for each target). It was only possible to get this data analyzed in the psych package in R and I’m not exactly sure whether I am able to interpret the output correctly. I assume I could simply remove the empty cells but I’m not sure if that would be appropriate. Any thoughts on how this could be analyzed in SPSS?
Yes, it can be done. You would need to run an ANOVA on the long-form version of the dataset (with each observation as a case) and then use the formulas presented by Shrout & Fleiss to calculate ICC(1,1) and ICC(1,k), with k being the average number of raters per independent case. If you read up some comments, you will see that I was planning to put together a tutorial on this but still haven’t gotten around to it!!
Dr. Landers
Excellent article and discussion thread. Thank you for this resource.
I have a question about the use of IRR and averaging dichotomous items (1=present vs. 0 = absent). We have 5 raters evaluate the presence vs. absence of 7 features in 100 photos (not a scale). The raters do not evaluate more than one photo or feature in any photo.
We don’t intend to rely on any one rater’s score for any feature, but rather use the average score of five raters for each feature in a photo. If we’re interested in reliability of any individual rater’s score, a Krippendorff”s alpha seems appropriate, but if we intend to use the average score (e.g. 1, 1, 0, 1, 0 = 0.6) for each feature and want to look at the reliability of the average scores, would ICC (1,5) be acceptable use?
James
No, I wouldn’t – ICC assumes normal distributions of ratings, and you have dichotomous ratings. ICC will be fine in certain circumstances given that, but it can also be highly misleading (e.g., if you have any raters that are even moderately lopsided from 50%). So given that, I would rely on a technique that doesn’t require distributional assumption.
Thank you for your thoughts. Any recommendation on a technique(s) that does not require a distributional assumption for average scores of these ratings?
Fleiss’ kappa is non-parametric; it is based on simple counts. I believe Krippendorff’s alpha is actually equivalent to kappa for nominal and ordinal data, at least with consistent rater counts; that is supposedly the draw of it, although I haven’t dug into the formulas yet; it is supposed to be a valid assessment of reliability regardless of scale of measurement.
Is there a need to conduct a power analysis prior to calculating ICC?
It depends on why you need the ICC. If you just want to report on the observed reliability of measurement in your sample, a point estimate of ICC is sufficient. If you have meaningful hypotheses to test about that reliability, e.g., that it is drawn from a population of particular reliabilities, then you’d need a power analysis for that.
Dear Dr. Landers,
thank you so much for this excellent article and discussion thread.
I have a question.
I did a study on mental health of school children and therefore have ratings on them from children themselves, their parents and teachers.
The prevalence of mental problems is 28% according to teacher, 13% according to children an 11% according to parents.
On a scale of „mental abnormal“ vs „mental normal“ I calculated the agreement between the rater-combos and as expected: With more raters there is less agreement.
The combination of all three raters had agreement that a specific child is „mental normal“ in 66% and that a specific child ist „mental abnormal“ in just 2%.
So in 32% of all cases there was not absolute agreement between the three raters, neither to normal nor abnormal rating.
Now I calculated the ICC for each rater-combo, to see which combo is most reliable. (calculation was done with the raw scores, not with „mental abnormal“ vs „mental normal“)
I got an ICC of 0.63 for parents/children, 0.42 for teacher/children, 0.55 teacher/parents and 0,66 for teacher/parents/children.
Could you explain to me, why there is (in relation to the other combos) such a „high“ ICC for all three raters, wenn I just calculated that they agree on „mental abnormal“ in just 2% of the cases?
I know I will be asked that question and I can’t give a proper answer.
I really really hope you can help me understanding this the easy way.
Thank you so much in advance!
I’m not quite sure what you mean by “agreement” if you did not calculate ICC to begin with, i.e., I don’t see where the 2% is coming from. If you mean absolute agreement in the sense that you checked whether ratings of one type were literally equal to ratings of another type (agreement on the “abnormal vs normal” dichotomous score), that is not a very good way to assess agreement unless that dichotomous score is itself clinically meaningful. Since you have Likert-sounding scales, I don’t think it is. Any time you convert a scale score into a dichotomous one, you lose a lot of information; straight percentage agreement is much less sensitive than ICC is. That is why you use ICC with scale data and % agreement (or kappa) with dichotomous data. That sounds like a situation where I would perform a lot of post-hoc data exploration to determine the reason behind that disagreement. There are many possible causes, only some of which you can investigate with the data you have.
Thank you for your quick answer.
Yes, I mean „agreement“ as absolute agreement at the dichotomous scale („abnormal vs normal“).
I wanted to list how abnormal the children are according to every single rater and according to all rater-combos.
I thought, this way (with ICC) I could show, that there is more real agreement between the raters than one would suppose by just looking percentage agreement.
Is that at least a valide assumption?
Probably the scale scores are close to each other (quite good ICC) but around the cut off scores for „normal“ vs „abnormal“.
Of course I can not investigate the real reason behind disagreement and one conclusion is that every rater has it’s very special view in a very special setting and is delivering only one part of the truth.
If there were only little disagreement between the raters, I could just use one.
What I don’t really understand is, why I often have a higher ICC with 3 raters compared to 2 raters? Is this to be expected? Could one assume the ICC to rise with 4 raters?
Yes, it is. ICC assumes that all raters are drawn from the same theoretical population and then assesses the degree to which they are rating the same construct. If you were to add a 4th drawn from that same population, you would expect ICC to increase by a predictable amount – you can actually use the Spearman-Brown prophecy formula to predict this value. If you added a 4th dissimilar rater, it could go either way. The value itself gives you the percentage of true score variance being assessed by the mean score of the raters; thus, adding more raters of the same quality as the ones you have will always make that mean score more stable.
Thank you so much, that really helped me understand.
Dear Dr. Landers,
I’ve read your interesting and exhaustive article, but I am unsure about how I should deal with the calculations of ICCs in my case.
The dataset look as follows:
center object (horse) rater1 (owner of the “object”) rater2 (coach of the object)
a 1 rater (a)=20 rater (b)=21
a 2 rater (a)=… rater (c)=…
a 3 rater (d)=… rater (e)=…
b 4 rater (f)=…. rater (g)=…
b 5 rater (f)=… rater (h)=…
b 6 rater (f)=… rater (i)=…
c 7 rater (l)=… rater (m)=…
c 8 rater (n)=… rater (o)=…
c 9 rater (p)=… rater (q)=…
The literature using the same instrument reports two-way Fixed ICCs with absolute agreement (single scores).
I am not sure the ICCs calculation is correct. I would appreciate your advice about this situation.
Thank you in advance!
You don’t really provide enough information to evaluate that, so I don’t know. I will say that fixed seems like a strange choice because it assumes that the particular set of owners and coaches you have are the only owners and coaches you would ever be interested in generalizing your conclusions to. It seems more likely to me that your study is examining a sample of owners and coaches. But I don’t know your literature, of course. Single-rater ICC would also be an odd choice because it assesses the reliability of a single rater, but you appear to have two populations of raters, so I don’t see how that could be meaningful.
Dear Dr Landers,
Thank you for your great explanation, I was wondering if you could answer a couple of questions with regard to a statistics query I’m experiencing, if you have the time.
As part of a larger study involving 2 raters who will be used interchangeably we want to ensure that the 2 raters are reliable both between eachother and with themselves at another time point. To determine this 2 raters assessed the same measurement 3 times on the same day (T1) and took an average. Then this was repeated 3 days later (T2). We want to calculate the interrater reliability of the two assessors at T1 and also calculate calculate the intrarater reliability of each assessor between T1 and T2.
My understanding is that we require a two way mixed ICC as the raters represent the population. However I am unsure whether to report single or average measures?
Any advice would be much appreciated,
Many thanks,
Sarah
If the raters “represent” the population, you want a two-way random ICC. If the raters “are” the population, you want a two-way mixed.
With this design, you have three sources of variance, meaning you have two options. You can either assess inter-rater, intra-rater, and over-time reliability separately with individual ICCs or you need to identify an alternative approach to measuring reliability. ICC cannot give an overall estimate of variance taking both intra- and inter-rater variance into account simultaneously. It sounds like you need to take a generalizability theory approach.
Hi,
Thank you for your post, it has been very useful. I have a query with regard to statistics on SPSS. I am running an inter and an intra-rater reliability test. I performed a test on 15 subjects on two separate occasions, and so did my colleague. We calculated the ICC using your guide but my supervisor would like a standard Error of the Mean score, as well as Minimal Detectable Change. To my knowledge, SEM is calculated using the formula below;
SEM = S sqrt(1-ICC).
I have the ICC value from doing an absolute agreement test on SPSS but I have two SD values for Session 1 and for Session 2. I don’t know which SD to use in the formula.
Any feedback would be greatly appreciated.
Thanks,
Aoife
SE of the mean (SEM) and SE of measurement (SEm) are different calculations. You said “mean” but your formula is for “measurement.” So I am not sure what you’re trying to do. The formula for SEm is actually SEm = SEM(sqrt(1-ICC)) formula, S represents the standard error of the mean, so you need the SE of the mean to calculate the SE of measurement. SEM = SD / sqrt(N). In both formulas, the SD or SEM is calculated using the SD of the number that you’re actually using, which is the per-case mean score. So you can calculate SEM by using COMPUTE to calculate a mean of the two scores in your original dataset and then calculating the SD of that value and using it in the SEM formula. Then use that SEM in the SEm formula above for whichever ICC you want to know about.
So, if your ICC was .5 and the SD of the rater mean score was .3 across 15 cases, you’d have:
SEM = .3 / SQRT(15) = .07746
SEm = .07746 * SQRT(1-.5) = .05477
Hi Dr. Landers,
Thank you very much for your response. I apologize that I wasn’t very clear but you are right that it is the SEm that i was looking to get. I suppose my greatest difficulty in getting this was not knowing if I should use the mean and SD from Session 1 or from Session 2, or even take both those means and just take the average of the two together. I’m not very familiar with SPSS so I’ve a lot of work to do on that front.
Thank you sincerely for your help, I really appreciate it.
Aoife
I have written an article about accuracy of digital palpation to show correctly the place of cricothyroid membrane. I made power analysis from an article in literature according to patient number. I got comment on that your article includes 20 raters , literature article includes 41. But our raters made 4 observations on diffferent patients. although literature raters made only one. In this case I thought that I am not underpower. What is your opinion?
I think you are mixing some concepts together. Power is not a concern except in the context of inferential statistics, i.e., null hypothesis significance testing. If you are interested in testing a hypothesis about rater agreement, you will need to have a specific predicted effect size to calculate power. Power differs by both sample size and predicted effect, so you need to assume values for at least 2 of those to calculate the other. If you are just worried about the accuracy of your ICC estimate, then you are instead concerned with the width of the confidence interval surrounding ICC, which is related to power but is not the same thing. In that case, you should target a rater sample size that brings the standard error down to a particular, desired level, and you should have a good reason for choosing that level.
All inferential statistics that do not find statistical significance are by definition “underpowered” for the effect that was actually observed.
Hello,
I was wondering how you would write those results in apa format?
Which results? In APA, simply reporting an ICC is typically in the format used here, e.g., a cite to Shrout & Fleiss near something like: ICC(2,3)=.8. Think of an ICC as a type of effect size, reporting-wise.
Dear Dr. Landers,
in the process of developing physical performance test, I used to 2 examiners (A and B) to test a sample of patients in two occasions independently, but simultaneously. Examiner A was the rater who administered the test, while examiner B was the co-assessor who rated the performance only in the first occasion. in the second occasion we used the same examiners at similar time of the day. However, examiner A was the co-assessor and examiner B was the rater. We investigating inter-rater, intra-rater reliability and measurement error. Firstly, is that correct to use the ICC2,1 (model: Two-Way Random and type: absolute agreement) as a parameter for inter/intra-rater reliability and the SEM as a parameter for the measurement error? Secondly, how to get the variance components such as σ2p, σ2pt. and σ2 error in order to calculate the SEM
Best regards
ICC(2,1) will tell you the reliability of a single rater, i.e., an imaginary person that would be considered a “typical” examiner, given your various examiner pairs. So if that’s what you want to know about, then sure. If your goal is to use the mean score for anything, you would need ICC(2,2) instead, which refers to the reliability of the average score itself (A+B/2). I am not sure in what formula you plan to use these various sigmas you are asking for, but if by SEM you mean standard error of the mean, that is quite easy with the SPSS output – simply subtract the ICC from the upper bound of the confidence interval and divide by 1.96.
Hello Dr,
Hope you are doing fine
For my study to assess the IRR, i am using both the weighted kappa and the ICC
Concerning the ICC i am finding difficulty in finding the interpretation the average measure of the ICC whether this number yields a good or or poor outcome .
Some told me to use the Cronbacks alfa as a reference to build up conclusion about the average ICC number;
I am using the ICC : Two-way mixed effects model where people effects are random and measures effects are fixed ( Type C)
So if you can guide me to which reference or the normal range for the ICC with the reference it would be beneficial so i can add it to my thesis project
Your help is appreciated,
Reliability estimates are reliability estimates. If their assumptions are met, they are interpreted the same way: the ratio of true score variance to observed variance. So whatever standard you usually use for reliability is the same here.
Thanks for your reply,
Concerning the ICC result, how shall i interpret it if it is good or excellent reliability based on what reference range?
Dear Dr Landers,
I would be very grateful if you could advise me on a statistical analysis I am trying to undertake.
As part of a research project, I am looking at the comparability of questionnaire scores between parents and children. There are 30 parents and 30 children. There are about 50 items in each questionnaire (the items are the same on both versions, just worded differently, i.e. my child is … verses I am). Both parents and children are answering questions in relation to the mental health of the child.
I think that using intraclass correlations here is appropriate, but I am not sure whether I need to do item by item comparisons or whether this should be done using the overall total score. I have calculated intraclass coefficients for each pair, using raw data scores for each item and have used these to calculate a ‘mean’ intraclass correlation for the overall group. Do you think that this is the best way to do it?
Many thanks,
Rebecca
There is currently unfortunately no straightforward way to look at these two sources of variance (inter-item and inter-rater) simultaneously. The most common framework is generalizability theory, which involves decomposing the overall ratings into their individual sources of variance. If you don’t want to do that, the next option would be to assess inter-item reliability and inter-rater reliability separately, i.e., by calculating an ICC(2,k)/Cronbach’s alpha on the items in the scale, and then to calculate ICC(2,1) on the scale means themselves. Since there are 50 items, it sounds like there are multiple scales within your questionnaire; in that case, you’d want to repeat this process for each construct, individually. If there are 50 DVs, then you would need to look at it purely by item (with no inter-item reliability).
Assuming you have constructs, as to whether or not item-by-item comparisons is appropriate in addition to that, that depends on what you plan to do with this information. But at the end the of day, the basic call is simple: if you need to know the reliability of individual scores, calculate them; if you need to know the reliability of scale means, calculate that instead.
So in your example, you have calculated ICC for 50 items and then looked at the mean ICC. I would interpret that number as “on average, the mean true score variance contained in each of these items is .xxx”. Is that what you want to know? If so, you’re fine. If you want to ask, “what proportion of the mean overall mental health score is true score variance?” then what you have done does not tell you that.
Dear Dr Landers,
Thank you very much for your blog and I have a question which made me confused though after reading your paper.
I would be grateful if you can answer me the questions.
I have done a survey in a company with 47 groups and 217 members in total(some groups have just 3 members and other have more than 10).
For the purpose of aggregating the organizational justice (3 items,individual rated) to group level, we need to calculate the Rwg and ICC(1) and ICC(2).
For the Rwg, the median is .85, and value of Rwg are larger than .70 in more than 80% of the 47 groups. This indicate that members in most group have high agreement about the justice.
After that, I calcuted ICC(1) in the SPSS, following your advice, I put the data in the following format:
Group Item1.1 Item1.2 Item 1.3 Item 1.4 Item 1.5 Item 1.6 …… Item1.13 Item2.1 Item2.2 Item 2.3 Item 2.4 Item 2.5 Item 2.6 …… Item2.13 Item3.1 …… Item3.13
1 3 3 2 999 999 999 …… 999 3 2 3 999 999 999 999 2 …… 999
2 4 2 2 2 1 3 3 2 1 2 3 4 3 2 3 2
3 3 3 2 4 4 999 …… 999 3 3 2 4 4 999 …… 999 3 …… 999
……
47
(Some explanation of the data format above
1.Gruop are the 47 groups in colomun;
2.Item 1.1 -1.13 means there are maximum 13 members in some group,here Group 2 has 13 members, and members are 3 for group 1 and 5 for group 3;
3.for the 999 it represents missing values.)
After that,I click the button in the following in SPSS 24.0, Scale–Realiability Analysis–Statistics–Interclass Correlation Coefficient–One-Way Random, but the SPSS
shows Warning as ” There are too few cases (N = 1) for the analysis. Execution of this command stops.” . I don’t know why.
The condition are the same whether I choose data of ” Item 1.1- Item1.13″ or “Item 1.1-Item 3.13”,which separately means to calculte the ICC(1) for Item1 and Item1-3.
It is because the ICC analysis in SPSS cannot handle missing data; it uses listwise deletion. If you want to calculate ICC in the presence of missing data, i.e., with unequal group sizes, I would suggest software capable of analyzing hierarchical models, such as HLM or the lmer library in R. The analysis SPSS does is intended for assessing reliability only.
the data set format is a little confused due to the typesetting, so I will type it again here for your better understanding.
Group A1.1 A1.2 A1.3 A1.4 A1.5 A1.6 A1.7…… A1.13 A2.1 A2.2 A2.3 …… A2.13 A3.1 ……A3.13
1 2 4 3 999 999 999 999 …… 999 3 4 2 …… 999 3 …… 999
2 3 2 1 2 3 2 3 …… 3 3 2 3 …… 4 3 …… 4
3 2 3 2 3 2 3 999…… 999 4 2 2 …… 999 3 …… 999
Just Above, in Am.n, m means the three dimensions of justice ( 1,2,3 SEPERATELY) , n means the subject number (1-13, different in different group,such as 3 members in group 1, 13 in group 2, and 6 in group 3)
Dear Dr Landers,
Thank you very much for your reply ,I have tried your answer and it’s right! I am grateful for your advice from China.
But still a little question, I don’t know whether you have read the paper “Answers to 20 Questions About Interrater Reliability and Interrater Agreement ” , the method I have used is from the attachment from the paper, and I have checked it that if just one group has the maximum member, the SPSS will just count 1 case and no result, but if more than one team has the maximum member (e.g if there are at least 2 groups of 13 members in my data) ,there would be result. if so , the results will have great bias?
and are there any method to change the “listwise” such as SPSS syntax?
Sincerely yours, Jichang
Yes, this approach will not produce the ICC you want. There is no way to do this in SPSS without creating the ANOVA manually and calculating the ICC estimates by hand following the instructions given by Shrout & Fleiss (cited in this article).
Thank you very much and I have shared this website to my classmates, very useful website for us students.
Dear Dr. Landers,
I am conducting research study which involves aggregation of individual level responses to organization level variable.
For instance, I have collected data of employee engagement having 6 items and 3-5 raters from each organization rate on 5 point scale (ranging 1-5). Now, I have to aggregate individual responses into organization. For said purpose, I have calculated ICCs by using ANOVA as suggested above including ICC (1) and ICC (2) with one-way-random consistency but I am not sure. The result shows values ICC(1)=.30 and ICC (2)=.72. Please confirm the acceptable range of both ICCs as different papers mention value of ICC (2) > .70 but I am still not clear regarding ICC (1) value. Please guide.
Similarly, I have collected data of entrepreneurial orientation having 9 items and 3-5 raters from each organization rate on 5 point scale (ranging 1-5). Now, I have to aggregate individual responses into organization. For said purpose, I have calculated ICCs by using ANOVA as suggested above including ICC (1) and ICC (2) with one-way-random consistency but I am not sure. The result shows values ICC(1)=.37 and ICC (2)=.85. Please also guide whether the number of questionnaire items also impact on the value of ICCs specially ICC (1).
Need your kind guidance.
Profound Regards,
Athar Rasheed
In the terms of this article, you are probably referring to ICC(1,1) and ICC(1,k).
Assuming that, there is really no “correct” answer to these questions. I recommend you take a look at similar articles published in your subfield, preferably within the journal you are targeting, to see what has been deemed acceptable before. But in general, ICC(1,k) is reliability of the mean score whereas ICC(1,1) is the reliability of individual raters. ICC(1,k) will generally become larger as long as you keep adding raters but ICC(1,1) will only become more accurate. So the lower ICC(1,1) is, the less people tend to agree with each other.
Whether individual people within organizations agreeing with each other is meaningful to you is a domain-specific question that you should answer for yourself.
It was an excellent read. Perfect for my level of understanding of stats. My question is not directly related to the post, but i will truly appreciate your help. I’m a clinical pharmacologist.
I need to find sample size in a study where I develop a new assay to quantify a drug concentration in blood and correlate with the measurements done by a established gold standard assay.
Is ICC based sample size calculation the right method? Is there any better method?
The reason for my doubt is because I know for sure that the gold standard method is perfect. It is not the agreement between 2 raters but the actual deviation of one method from the truth.
Kindly give your opinion.
Thank you
I would say probably not. ICC assumes all raters contain and contribute error. If you are comparing a rater to a gold standard, you probably want something simpler, e.g., deviation and rank order comparisons.
Dear Dr. Landers,
thank you for this extensiv article!
I have some questions left in my special case.
I have a questionnaire answered by different teacher and parents. So a lot of different teacher made ratings to the pupils only in their class and the parents of these pupils did the same by themselfes.
Because the pupils were chosen randomly and the selection of parents and teachers is determinated by the pupils, I would choose the two-way mixed model of ICC.
But do I look at the average measure or single measure? Because each data-point in my SPSS file is from a single teacher and not aggregated from different persons, I think “single measure” would be correct.
In the end I’ld like to generalize the ICC to “parents” and “teacher” in general. Is this possible?
Thank you so much in advance.
Best regards, Tom
You can only assess reliability if you have replication of ratings of a single target by multiple sources of the same type. To assess the reliability of teachers, you need at least two teachers per student making ratings. To assess the reliability of parents, you need two parents per student making ratings. If you combine parents and teachers into a single reliability analysis, you are saying that a parent and a teacher are each random samples from a population of raters.
Thank you for your reply.
But isn’t ICC an appropriate method to explore inter-rater agreement between teacher-parents and parents-pupils and teacher-pupils, for example? There is a self-rating of pupil A, a rating of one teacher to pupil A, and a rating of the mother of pupil A. Isn’t it correct that I could generate an ICC of the Rater-Combo teacher-parent and so on? My aim here is not to the assess reliability of one of these raters but to explore the agreement of two (or three) raters against chance. If so, would this scenario need the average measure or single measure?
Sure, but because it’s not reliability, then the guidelines stated here don’t apply the same way. You are talking about the multi-level measurement context, in which case both single and average raters tell you slightly different things, and you should use the standards of the literature you are publishing in. In organizational psychology, where ICC most commonly crops up in teams and leadership research, you typically report both.
Okay, thank you, I’ll report both!
Do you find the two-way mixed model of ICC appropriate in this case?
No, you have different teachers and different parents for each case, so you want ICC(1,1) and ICC(1,k) – one-way random.
that was great. Thanks so much. but please help me out with this one.
Am using one rater on finding out the tasks types in two mathematics textbooks on two different occassions. what do I do?
It is impossible to assess inter-rater reliability in that case, although you can assess test re-test reliability. In that case, you can treat Time 1 as rater 1 and Time 2 as rater 2 and calculate some variation of ICC(2), depending upon your answers to the questions above.
Dear Dr Landers,
Appreciate your clear explanation on ICC. However, would like to clarify some doubts in my study.
I have 4 raters who are Markers A, B, C and D. Each marker has graded the same 33 essay scripts. I would like to test the agreement on scores awarded by the four markers on a single essay question provided to test the reliability. Do i use ICC (3,1) since I am comparing the scores of each essay script among the four markers? Or do I use ICC (3,33) since I will be comparing all the same 33 essay scores among the four markers. Kindly advise.
Thank you:)
Hi again Dr Landers,
Please refer to my earlier message as this is a follow up of that.
Sorry, I just realised that if I am not wrong, my ICC type should be ICC (3, 4) since the markers are fixed raters in the study for every ratee and the agreement is to be measure across the 4 markers and NOT the 33 essay scores(ratees). Sorry for the earlier message due to misunderstanding. Kindly advise if i got it right this time. Thank you Dr Landers 🙂
If you are only interested in the reliability of the average score across these four specific people, then this is correct. If you are interested in the reliability of any one person (e.g., to see if you could replace the 4 with 1 in the future and maintain accurate measurement), you’d want ICC(#,1). If you want to know the reliability of this approach instead of the reliability of these 4 specific people, you’d want ICC(2,#).
Dear Dr Landers,
Thank you so much for the prompt & intelligible response Dr Landers. Really do appreciate your assistance, clear guide, explanation and time! God bless
Dear Dr. Landers,
Thank you for your article on how to compute the ICC in spss.
I’ve computed it succesfully, however one of the ICC’s is negative.
Can you give me some global insight in how the ICC is computed, so that I can interprete these results in the right manner?
Additional information:
For my dissertation I have undertaken an experiment whereby a control- (n=35) and experimental group (n=37) have assessed the same object on 4 criteriam, each with a 5 point-scale. The ICC(2,1) of the experimental group is -0.005.
Thank you for your help in advance.
With kind regards,
Arno Broos
University of Twente
You can find the full calculation for ICC in the reference cited. It is calculated from ANOVA output.
When your ICC is negative, one of two things is likely: 1) you have exceptionally severe disagreement or 2) you have not met the assumptions of ICC, i.e., your scores are not normally distributed. Even with a 5-point scale, your disagreements may be essentially dichotomous. In such cases, you should use a reliability estimate that does not require normality, such as Fleiss’ kappa.
Dear Dr. Landers,
Thank you for your quick response to my last question.
Indeed, the data was not always normally distributed, which is probably the cause for the negative ICC. Now I am using the Fleiss Kappa for my calculations.
Another question:
I also want to calculate the ICC when using dichotomous data (Fail-Pass) since this concerns a high-stakes assessment. I have wondered around on the internet but failed to find a way to calculate the ICC for dichotomous data for multiple raters on a single case. Can you help me?
Thank you for your help in advance.
With kind regards,
Arno Broos
University of Twente
You should still be able to use ICC on dummy-coded (0,1) data but you can’t interpret it quite the same way, since you are (as before) still working with non-normal data. It is a similar problem as with coefficient alpha – if you use the alpha formulas on binary data, you’ll get an alpha that is also called a “Kuder-Richardson 20” (KR-20). The reason you might label it a KR-20 and not alpha, however, is because KR-20 tends to under-estimate reliability because of the normality assumption violation. The same will be true with ICC done on binary data (which makes sense, since ICC [2,k] = alpha).
Dear Dr. Landers,
Thank you for the thorough explanation that continues throughout the comments.
We are working on our master’s thesis and after reading all explanations, we’re still not sure which kind of ICC should we use.
We have 51 subjects for which we rate interviews on one measure and videotaped interactions on 6 measures. We are 4 raters. All 4 raters rated the same part of the data (11 interviews, 8 interactions) and the rest of the data was then divided between raters, so that only one rater rated each of the remaining interactions/interviews (the interviews were rated by only 3 raters from the 4 who’ve done the common ones).
We want to calculate the ICC on each of the measures.
So, we understand we need to use the single meausre and not the average (even though for the common subjects we used the average as the final score), and that we are a sample of raters.
But, regarding Q1 we’re unsure – do we need to regard only the ratees we’re doing the ICC on (the common 11 and 8), and then the answer is YES, or the entire sample, and then the answer is NO?
Thank you!
Michal & Aya
If you used the average as the final score, and you want to know the reliability of that average, you do want average measures.
You need to answer Q1 for each ICC, so it depends. Remember that ICC reflects the reliability of a specific mean score – was that number calculated with consistent raters for every case or not?
Thank you for your quick answer! I will try to clarify the situation.
We only used the average as the final score for the subjects we all coded. for the rest, we used a single score rated by a single rater.
So, we can only calculate the ICC on the few subjects we all coded – they were all coded by the same consistent raters (so, Q1=YES); but we want to generalize from that score to the reliability of all scores. Actually, the most were rated by a single rater from the same group of raters. (so maybe then Q1=NO?).
Thanks again,
Michal & Aya
Ah, I see. In that case, you have estimated with two different reliabilities. The mean scores, where you have them, are described by ICC(2,2) whereas the lone scores are described by ICC(2,1). Since mean scores are more reliable, you probably want to use mean scores where you have them and lone scores where you don’t, but this means that your variables have varying reliability within themselves. In these situations, people sometimes just report the single measures estimate and call it a “lower bound estimate of reliability” since it doesn’t take into account that you have multiple raters for some cases. But it will depend a bit on how sophisticated your research literature and thesis committees are as to whether they understand this in the first place, accept this as a middle ground as far as what you’re trying to do in your study, and/or require a more complete approach (such as generalizability analysis).
Regardless, it’s important to realize that when generalizing from multirater estimates to single rater contexts, you must make the assumption that there are no systematic differences between the cases with multiple raters and the cases with a single rater. If there could be (and you describe one such potential difference: that most single ratings were by the same person), then you should not generalize the reliability estimate from cases you double-rated to cases you single-rated. Generalizing from double-rated to single-rated using the single rater ICC is ok as long as you are confident in those assumptions: 1) that future raters are prototypical of the original rater population and 2) that future cases are prototypical of the originally rated cases.
This added complexity by the way is why people typically try to have all raters rate all cases – they are much easier data to work with and requires fewer assumptions.
Thank you so much!
Since we are sure about those assumptions, we will use ICC(2,1) and report the single measures as the lower bound estimate of reliability.
We have one more question. In one of our measures, we got a low reliability for the single measure (0.344) even though the scores between raters seem to be quite similar. what could be the reason for such low reliability? perhaps if they are too similiar it hurts the reliability in some way?
It is usually because raters do not provide normally distributed data.
Thanks for the info! I have an aggregated data and needs to calculate inter rater agreement (rwg), can you please show me how to do it with spss? Thank you.
Hello, I have a data set with parent and teacher ratings of students. The data was collected at 2 time points from Grade 3-4 and Grade 5-6. Parents of students do not change over time but teachers do. The experimental rating tool has 9 items with a 3-point likert scale (not able, able, more than able). There are no established psychometric properties.
Goal: To conduct a preliminary analysis on the nature of parent & teacher ratings.
Question: Would it make sense to recode the data (from -1,0,1 to 0,1,2), restructure the data from wide to long format and then compute the correlation and ICC on total scores? If so, what would be the correct model in SPSS and what should be reported?
Thank you in advance for any advice you can provide!
You essentially have a matrix of relationships; you have teachers multiple times in the dataset, but time and parent dependencies. I would not do this in SPSS, and I would not use ICC (at least alone). You have a multilevel dataset; I would suggest approaching it with multilevel modeling.
Dr. Landers,
Thank you for the time you spend supporting so many people with statistics!
I need to evaluate the interrater reliability of 2 raters rating each sentence produced by my 8 participants in conversation (rating whether subject-verb structure is intact or not, so binary +/-). Each participant produced 100 utterances that are rated. Is it appropriate to a) average the accuracy for intact production, arriving at one data point per participant, and then running the ICC on the ten participants using each individual’s average score from each rater; OR b) to run a Cohen’s Kappa using the individual binary scores for each of the 100 utterances for each of the 8 participants, resulting in 800 datapoints rated by each of the two raters?
THANK YOU so much — this seems like such a simple question and I can’t find the answer anywhere!
Marion
That’s actually a pretty complicated problem. You have multilevel binary data. So it depends upon what your analysis will actually be on. If you are only running your statistical analyses on the 100-utterance averages, i.e., you never run analyses on binary data just on aggregated ratio level data, then you want the ICC approach. Or in other words, your ICC calculation technique needs to mimic your data cleaning approach for your stats at the final step.
Hi again Dr Landers,
Thank you for your continuous support.
Appreciate your professional advice on the following output from SPSS.
I’m using ICC (3,2), two way mixed methods and two fixed raters in my analysis.
The result I obtained using SPSS is as follows:
Intraclass Correlation Coefficient
Intraclass Correlation 95% Confidence Interval F Test with True Value 0
Lower Bound Upper Bound Value df1 df2 Sig
Single Measures .547 .241 .755 3.741 29 29 .000
Average Measures .707 .388 .860 3.741 29 29 .000
ICC (3,2) is at 0.707, which is good but noted that the lower bound CI is only at 0.388. Could you please explain the probable reason for that?
Fyi, I have 30 ratees and two fixed raters.
Thank you Dr Landers.
The lower bound is a lower bound confidence interval, i.e., 95% of samples created by these two raters making ratings would be reliable between .388 and 1.000. The wide range reflects estimate instability. The only way to narrow a confidence interval is to collect a larger sample.
Thank you, Dr. Landers, for your article and the blog here. I find both particularly helpful. However, I would like to be sure that my approach to ICC is correct. In our studies, we typically present participants (here n=80) with two visual stimuli and observe their looking times. Looking times are coded directly during the experiment (first coding), and again from video (second coding). Therefore, we have two coders per case but several different coders both for the first as well for the second coding. Coders are trained interns, and all 320 cases are second coded. We want to know if first and second coding agree, irrespective of the performance of the individual coders. Assuming that they are from the same population, I conducted an ICC(1,2) creating one data set per variable (which is the looking direction), cases in rows, coders in columns, yielding all ICC’s above .9. Is this correct? And is it exhaustive? Thank you for your patience!
If I’m reading this correctly, you have 80 participants with 2 stimuli with 2 ratings per stimulus; thus, a total of 320 ratings, which can themselves be split up into just 2 sources (160 of stimulus 1 vs 160 of stimulus 2). As long as you are comfortable saying that your coders are chosen at random, and that your coders are all essentially interchangeable with each other, then ICC(1,2) is the correct way to evaluate reliability in this case. You would indeed have two ICCs, one for stimulus 1 and one for stimulus 2. So that sounds correct to me.
I would not say it is exhaustive, since you might want to also evaluate whether your raters are in fact interchangeable rather than just assuming it, e.g., by looking for mean differences between raters. But it is probably not necessary given the high ICC and low k, at least assuming you are looking at an agreement ICC and not a correlational ICC.
Dear Dr. Landers, thank you for your quick response and your willingness to help. To clarify, we have two stimuli and two trials (essentially measurement repetitions with the location of the simuli counterbalanced), resulting in 4 data points per participant. By taking the mean values over the two trials for each stimulus, I reduced the four data points to two (one per stimulus). Is this approach OK (a), or should I (b) calculate and report ICC’s for all data points separately? Or would it be better to (c) first calculate the separate ICCs and then average those across trials?
We had five coders, two of them doing first and second coding, the others only second coding. First and second coding were never done by the same person. I made one column for the first coding containing observations from coder 1 and 2, and one column for second coding, containing observations from all five coders. Is this approach (A) correct if we are only interested in an overall measure of inter-rater agreement? Or do I have to (B) make separate columns for each of the 5 coders (even if that would result in empty cells for most of the cases where this person was not coding – is that OK?).
If I – as you suggest – “want to also evaluate whether raters are in fact interchangeable rather than just assuming it” do I have to choose the latter approach (B)?
Since you have different coders doing different codings, you’ve actually confounded coding occasion and coder identity (1-2 vs 1-5), so it won’t be possible to evaluate if raters are in fact interchangeable. It will need to remain an untested assumption. The only way to test this is if you have replication at random across occasions, at least for ICC.
As far as I understand your dataset, ICC may not actually be appropriate since you have many more sources of variance per rating than is typical for ICC: rater, rating target, time, trial number, error, etc. If you want to really understand your ratings, you’d need to use a generalizability theory framework to decompose the observed variance into all of these sources.
Otherwise you can do it the way you’re doing it; you just need to be comfortable with all the information you’re losing by collapsing ratings so many times/ways.
Dear Dr. Landers, many thanks for your response and your support, it has been really precious. I will make an attempt to build a model considering the sources of variance.
Hello Dr. Landers,
Thank you for writing this article on ICCs. My apologies if this question has been asked previously (though it sounds comparable to Martina’s inquiry).
Our lab did a study looking at the reliability of different mathematical methods for calculating aerobic energy production within skeletal muscle during exercise. We have one ‘gold standard’ method and 6 other methods that we are comparing to the gold standard. Measurements were collected in 9 participants at 4 timepoints during exercise (i.e. 36 measurements for the gold standard method as well as the 6 methods that are being compared to the gold standard).
In short, I think we have a random(subjects)-fixed(method)-fixed(timepoint) setup. I ran a 2-way Mixed-absolute ICC in SPSS but we think this may be inappropriate because we have not accounted for the fact that some of the measures are repeated (timepoints, 4).
Is this a setup that cannot be run as an ICC? Or could I average the 4 timepoint measurements for each method/participant to remove the repeated measures component?
Thank you for your help.
All the best,
Miles Bartlett
You are correct that ICC is inappropriate, although possibly for a different reason. ICC assumes that all of your raters are interchangeable; if you have a gold standard, you can’t really use ICC. It is arguable that you could use ICC to assess covariance with a gold standard if you had exactly two raters, but with more, there’s no way to disentangle covariance between non-gold raters and between non-gold and gold. I suggest a generalizability theory approach.
Hi Dr Landers,
Thank you so much for your post.
I am new to ICC and wonder if you can help me with some questions?
I am carrying a test-retest reliability (2 trials) analysis using 10 subjects for this preliminary study. There is only 1 rater and i used ICC(2,1). I tested normality of the 10 subjects during the first and second trial. Data was not normal. I did a square root transformation and then data was normal. I carried out ICC using the transformed data. I wonder if this is correct?
I guess for my case, since there are two within subject trials, there is no concern for homogeneous variances. I wonder if this is right? I guess in future for 3 trials and above, sphericity assumption is required. If so, may I enquire how this sphericity assumption will affect the ICC if I am not interested in the CI?
SPSS gives the F test results (wrt zero) and I wonder if this has to be significant if I am not interested in testing this? I read elsewhere that the ICC test is not valid when F test is not significant and am confused why this is so.
Thank you very much for your time.
Thank you once again,
PT.
If you are assessing reliability across trials, trials are your “raters” as far as the analysis goes. Which ICC you need depends on your goals with the analysis. ICC(2,1) would control for trial-related variance (i.e., systematic differences between trial 1 and trial 2) and also give you the reliability of a single trial. The transformation is fine.
The F test tells you that there is meaningful between-rater variance in comparison to within-rater variance. If it is not statistically significant, it implies that you do not have sufficient evidence to conclude that the reliability of your trials is greater than 0. This is likely due to your sample size; with N=10, you’d need extremely high reliability (i.e., a large effect size) to detect it with an F test. You probably need a larger sample.
Thank you Dr Landers.
Hi Dr Landers,
I have conducted a cluster-randomized control trial (with baseline and followup measures) and I would like to calculate the intracluster correlation coefficient (ICC) at baseline. I would also like to estimate the 95%CI of the ICC. I have 8 clusters and approximately 8 subjects within each cluster.
How can I do this on SPSS?
Thank you,
Mitch
I would suggest by using the instructions in this article.
Thank you Dr Landers
While I was reading the article you’ve provided the link, I noticed that you’ve sent the article to the journal after they had already published it. It reads DATE RECEIVED: June 16, 2015 (on the left-hand side column of the paper) and LANDERS The Winnower JUNE 09 2015 (on the bottom of the page). It impressed me much to have such a success that you had!
They’ve published your article a week before you sent it!
Congratulations.
I am working on a project, in which we asked 5 raters to evaluate a bone dyplasia. All raters evaluated the dysplasia between o and 3.
0: normal
1: mild dysplasia
2: moderate dysplasia
3: severe dysplasia
All raters evaluated same specimens in 2 different time points. We want to report intra and interrater ICC.
I finished the initial anaylsis using SPSS.
What I wanted to ask was, whether I needed to report single measurement or average measurement?
Thank you!
It depends on what you want to know, per the questions above. Single-rater is the reliability of a single rater/time, i.e., if you randomly picked one rater’s score, what is their reliability? Average is the reliability of the mean score of all raters. So you want single for some reporting purposes and average for others.
Thank you for the very clear and helpful info. I have a question about inter-rater reliability for a multi-item scale. I have a 10 item scale, and each item identifies a characteristic as either present or absent. Is there a way to calculate inter-rater reliability between 4 raters accounting for which items they indicated were present, not just the number or sum of items indicated as present. Each of the 4 raters rates each participant, and the 4 raters are a sample of raters
You can just calculate reliability on the individual items, as long as at least 2 raters assessed each item. Just calculate the reliability of whatever you want to know the reliability of.
Dr. Landers,
I am a PhD student trying to do my research in the field of strategy within my organization. I have collected data at multi level within my service organization consisting of teams. being from an IT services organization, I have collected data from Team Manager and Team members.
The Team Lead questionnaire consisted of 65 questions measuring various scales including Team performance, Strategic Learning, Training etc.
Team Member questionnaire consisted of another 65-70 questions measuring various scales including Team performance, Learning behavior, team preparedness etc.
I now have responses from 255 team leads and from 1011 Team members reporting to these 255 leads. The responses are such for some team Leads only 1 Team member has responded and for the rest, of the leads two or more have responded (varying from 2 thru 7 people).
I am NOT doing multilevel analysis, instead, I am planning to keep the data at Team level and aggregate the team member data at the project level and then do the analysis of my models at the project levels. To do this, I understand that I have to perform intraclass correlations (ICC
2), within-group reliability statistics (rjg) to determine if the ICC2 coefficients and the interrater reliability coefficients (Rjg) are above 0.7
My Team Level output file contains 65 Columns ( having 65 questions measuring about 7 or 8 constructs including team performance) and has 1181 row (with one one row for each participant response belonging to one of the 255 project leads from the team leaders who have responded).
I just wanted to check with you on the following Sir.
1) To do the Intraclass correlations, I assume that I should pull each of the Scale (with all items) into a scale reliability analysis in SPSS (*ver 23) and then choose the option of Intraclass Correlation Coefficient and then I will get my results for the scale (to be done for all measurement constructs of Team member level – total of 1181 entries)
2) I am still not sure how to do the within-group reliability analysis to get the Rjg coefficients.
Can you pls let me know if I am in the right track of finding the ICC2 as mentioned in Step 1 above and also I would be grateful if you can help me with the process of doing within-group reliability in SPSS.
Thanks in advance sir.
Uma Shankar.
I would recommend calculating scale reliability statistics first (whatever they might be). Then calculate scale means, then calculate ICC for aggregations purposes on the basis of the scale means.
I assume by Rjg you mean within-groups R, which is really Rwg. Rwg cannot be calculated within SPSS to my knowledge (at least not without a lot of syntax). You can do it in Excel if you manually code all the computations or by using R. For R, you might check this function/package out: https://www.rdocumentation.org/packages/multilevel/versions/2.6/topics/rwg.j
Dear Richard
Many thanks for posting this tutorial, which has been exceptionally helpful to me. I’m currently involved in a project trying to understand inter-rater reliability in historical climatology. That is, the assignment of numerical values for climatic conditions to descriptive textual information on weather. Specifically, the project I’m involved in is looking at a number of years of descriptive data on rainfall conditions in 19th century Lesotho, taken from a different archives. Coders are asked to rank the rainfall in each year in a category from -2 (drought) to +2 (heavy rainfall).
I have conducted this exercise with over 70 different coders and your tutorial was very useful in determining both average and individual reliability. My overall aim is to see the minimum number of coders you require before you reach high reliability. My question is, therefore, is there a simple way in Excel to calculate the reliability from a sample of, say, 10 coders from my sample? I could course select 10 at random, but I have no way of knowing whether these are particularly good or bad coders within my overall sample.
My guess would be to take a random sample of 10 sets of coders and give a range of coefficients, but this seems both time consuming and not particularly statistically robust.
Many thanks in advance for your help.
Kind regards,
George Adamson
Once you know the #,k reliability, you can calculate the reliability of any number of raters using algebra alone, assuming “average” raters. This is actually how the #,1 reliability is calculated from the #,k reliability already in SPSS – it projects the reliability of a single rater based upon the reliability of all raters you have. The formula to be used is the Spearman-Brown prophesy formula, and I actually recommend the Wikipedia page, since it is very clear: https://en.wikipedia.org/wiki/Spearman%E2%80%93Brown_prediction_formula. You will want the first formula, predicted reliability. For your own sanity, I would suggest using the #,1 reliability as the input reliability and then select n based on the number of raters you want to project for. You can do it the other way around, but then everything is more confusingly proportional (e.g., if you calculate an ICC(2,5) and want to know the predicted reliability of ICC(2,4), your “n” term is .8, i.e., 80% of 5; if you start with ICC(2,1), then “n” is 4).
Dear Richard,
many thanks for your website. It was of great help, but I still have an open question. I´m currently planning a study on interrater reliability. I have a 4-order ordinal scale and potentially around 300 cases. Since coding one case takes some time, I wanted to use a different set of raters each time (so the one-way random model) and let raters assess around 30 cases. If Raters 1 and 2 would assess Case 1-30, Raters 3 and 4 assess Cases 31-60…would that be a possible option? I simulated data in SPSS assigning each rater 0ne column and SPSS gives me the error that no cases were available for the analysis. If you could help me, I would appreciate very much.
Well, two things. One, you would not want to assign raters that way, because it confounds case and rater identity, and two, when you have data for analysis, you should place them in 2 columns (per case: first rater, second rater).
For assignments, it sounds like you want each rater to rate 30 cases? That means you need 20 raters, and you need to randomly assign each to cases. You essentially need random number generation without replacement which is a bit trickier. Specifically, you need to randomly identify a rater between 1-20 for “observation 1” and then a second rater between 1-20 for “observation 2” but without selecting the number that was selected the first time. Here is an approach in Excel that could be modified for this purpose: https://www.got-it.ai/solutions/excel-chat/excel-tutorial/random/how-to-use-the-randbetween-function-with-no-duplicates
Hi there,
Thank you so much for writing such an informative post.
I have a question for you about the best way to handle a dataset I have. The data collection was such that I had 36 rooms of 8 raters who all rated 12 targets. Within each room, the raters all rated the same 12 targets — but the between-room targets were nonoverlapping.
I was hoping to calculate an average ICC for the entire dataset. Is the only way to do this to compute the ICC within each room and then average across all rooms?
Thanks in advance,
Em
You can calculate an average on any thing you might want, but it depends on why you want an ICC. A mean ICC is exactly that: the average agreement within rooms. I’m not quite sure what a room means in this context, but if you think rooms might meaningfully contribute variance in accuracy that’s substantively meaningful to you, then you’d want to include that. In such cases, you still need ICC, but in the framework of multilevel modeling (e.g., HLM). On first blush, it sounds like you have level 2 groups (rooms) and level 1 groups (raters) with a between-subjects level 1 factor (target ID), but you would need to work through the details of that to model it correctly.
@ Dr Landers,
Thank you for the awesome explanation on ICC.
Although the post seem way back, I still find it useful to me at a time like this. However, I have a question as regarding how to report my coefficient value. Unlike cronbach and few other models that gives a value of reliability coefficient (e.g Cronbach reliability statistics will bring out a table and we can deduce something like .92)
What figure do we tend to work with as the reliability coefficient for inter rater reliability from the table provided.
Thank you
All ICCs are reliability coefficients; in fact, the ICC(2,k) is a Cronbach’s alpha. In a sense, ICC is the general case of Cronbach’s alpha (and several other reliability/agreement statistics).
So the answer is: whichever number you think is relevant as the reliability estimate you’re after, given the guidelines I’ve provided here. If you follow the provided logic, you will end up the interrater reliability estimate you need.
Hi Dr. Landers,
I have a question that I hope you can help on for Inter-Rater Reliability. I have a survey where I ask raters to rate several behavioural statements on a Likert-scale. Their objective is to read each statement and indicate whether the behaviour “Does Not Improve Performance”, “Minimally Improves Performance”, “Moderately Improves Performance”, or “Maximally Improves the performance”. The survey measures multiple constructs, with each construct having 3-4 items.
I did a study where I asked 3 groups of raters (N=50 each), to rate their respective job (N=3 jobs) via the survey. I looked at Inter-Rater Reliability within each job group, and for each construct, to see the level of agreement. For the anaysis, I did Intra-Class Correlation Coefficients (ICC), Two-Way Random, Consistency, at 95% CI. I looked at ‘Average Measures’ as I am looking at the average score of the items measuring the construct.
Looking at the entire research sample (i.e. combining all 3 groups), the Cronbach alpha is around 0.7-0.8 for each construct, with the except of 1-2 constructs falling below 0.7.
Looking at the results for some groups, the ICC was quite high (above 0.8), but the 95% CI is very wide (e.g. 0.3 – 1.00), some of them even went negative at a very high number (e.g. -55.485-0.635, or -4.492-0.879), or some ICC are negative (e.g. -11.768). How should I interpret these results? Also, does this mean there is an issue with the items and definitions? Even though the Alpha reliabilities are sufficient?
Greatly appreciate your suggestions on how to interpret such results, and where the error may be.
A wide confidence interval is the consequence of either 1) small sample size or 2) relatively little meaningful variance in proportion to error variance. With rating tasks, it’s pretty common for a lot of raters to rate exactly the same thing. For example, if people are rating performance, they may have all rated straight 5s all the way across the survey. When they do that, there’s little-to-no variance in their responses for you to explain, so it appears as if agreement is poor. I suggest a visualization of your agreement data to see how bad the variance problem is (probably jitter plots).
I would also be worried about how you are conceptualizing agreement – you have two major sources of variance (rater and job) and it sounds like you are treating ratings as independent, which they aren’t. You will not get accurate ICCs anyway in that situation. You would be best off either 1) manually calculating ICCs but adding a job factor as a control variable or 2) determining ICC for each job independently, i.e., create 3 ICCs for each construct, one per job.
What you definitely can’t do is throw all 150 people into one analysis without addressing their non-independence.
Hi, I am writing my thesis and I have to calculate ICC (1) and ICC(2) which is required for data aggregation. I have 60 teams (N=250) that means I have 60 managers rating only their own team members (as each team represents a department) so 1st manager rates 3 members working with him and none other in the sample, 2nd manager rate his 4 members working with him and so on up to 60. For ICC(2) I am now confused how to calculate ICC (2) for this type of raters. Would it be same ICC(2) two-way random (absolute agreement) calculation as shown above or would this require another technique?
I am asking this question as I have used the Torsten Biemann Excel tool to calculate IRR and IRA. This tool is highly reliable and is in use by many scholars however, ICC(2) values I obtained from the tool are much more lower (0.70 for all constructs. What I do not understand is “Why the values would differ greatly?”
I will appreciate your suggestions and guidance on this.
The SPSS syntax I have used is:
RELIABILITY /VARIABLES = Item1.1 Item1.2 Item1.3 Item1.4 Item1.5
/SCALE(ALPHA) = ALL/MODEL = ALPHA
/ICC = MODEL(ONEWAY) CIN = 95 TESTVAL = 0.
EXECUTE.
LeBreton, J. M., & Senter, J. L. (2008). Answers to 20 Questions About Interrater Reliability and Interrater Agreement. Organizational Research Methods, 11(4), 815–852. https://doi.org/10.1177/1094428106296642
And the tool can be downloaded from the link below (refer to the thread- comment by Zinat Esbati)
https://www.researchgate.net/post/How_can_I_calculate_rwg_ICC_I_ICCII_in_SPSS
In teams research, ICC(2) refers to ICC(#,k), usually ICC(1,k). I don’t know anything about the Excel thing you did or how it is programmed.
Hello,
I found your page and responses very helpful. I am wondering if you could weigh in on a project I am working on. I am creating a new rating system for quantifying airway obstruction in patients with tracheostomies. I have a handful of pulmonologists and a handful of pulmonologists and otolaryngologists rating 50 images. The same 8-9 total people will rate all images. The scale has 2 questions, each with 4 levels that are ordinal. I am measuring the two questions separately because they do not pertain to the same underlying concept. I was planning on using ICC with a two-way random effects model, absolute agreement to assess interrater reliability. I also am re-testing everyone in 2 weeks, and I was planning on using 2-way mixed effects for absolute agreement to test for intra-rater reliability. Does this sound right?
I also wanted to know if you could do comparison testing with ICC or should I just do it based on the samples themselves. That is, I wanted to see whether the otolaryngologists and pulmonologists had different ratings overall. I think it would speak to the utility of this score if there wasn’t much difference between the two groups. I also think it would be interesting to note whether any particular photos or raters had more significant disagreement than others. Any thoughts on how to do this?
Yes, that sounds like a reasonable strategy for reliability at the first time point.
The re-test is more complex though – you would probably still want random effects (although I could see an argument both ways depending upon context), but a more fundamental issue is that you should probably assess them simultaneously, e.g., through a g-theory analysis. That would allow you to partial out time-related variance and rater-related variance, and also to model background (e.g., pulmonologist vs otolaryngologist), all simultaneously, which is importance since these effects may interact. You just have a lot more control over the specific nature of your modeling that way and thus the questions you can reasonably ask. But it is entirely different framework from basic reliability assessment.
So you would not do an ICC to test for intra-rater reliability, then?
I won’t pretend to be an expert on G theory… or really to have read anything about it before you mentioned it. But reading some primers on it, it sounds like I analyze each of the variables’ contribution to the overall variance in a single model with the variables of interest each being random effects (in my case pulm vs. oto, each instance of measurement, etc.). It seems like if my measure was continuous, some sources indicate I could do two-way ANOVA, but since my variables are interval, what do you suggest? Ordered logistic regression?
You can – it just leaves several other sources of variance unexplained, so that’s a limitation.
Is your measure not continuous? I thought you were capturing ratings? If your measure is not continuous, ICC is not appropriate anyway (it assumes normally distributed data).
My measure is of tracheal wall compression and obstruction. The rating is a 0 to 3 scale with 0 being 0 % obstruction, 1 being 1-50%, 2 being 51-99% and 3 being 100%. So it’s ordinal, no? To get really in the weeds, my measures are related to each other. The first measure is of tracheal wall collapse (percentages as above) and the second rating is of tissue occupying the residual airway. So if there is 25% tracheal wall collapse and a lesion that occupies 58% of the residual airway, the rating would be 1-2. I am examining the two ratings separately with the recognition that they are not FULLY independent.
I suppose I did not realize an ICC could not be used for ordinal data. I suppose I could use Spearman’s Rho to compare individual raters against each other, but I had seen similar rating scales use ICC for this. Is that incorrect?
It depends entirely upon how your field typically treats those data. There are strong norms within disciplines regarding treating ordinal data as continuous, both pro and con. If you have seen other researchers use ICC for this type of data in your literature, that would suggest to me that they are comfortable for whatever reason treating the outcome as continuous. Or perhaps they don’t really know what they’re doing statistically-speaking, which is not uncommon.
Technically speaking, agreement using ordinal data should be evaluated with a kappa, which does not have any distributional assumptions.
Rho is fine as long as you only have paired data (but I think you have more raters than that?). A rho is just a Pearson’s correlation on a rank-order transformation of your data, and a Pearson’s correlation is equivalent to an ICC(1,2), so I would think that a rho would be equivalent to an ICC(1,2) on rank data. And if you were comfortable with that, I suppose you could convert your dataset to rank data and then use ICC on the ranks. That’s quite a bit of extrapolation though, and I’m not sure I’ve ever seen it done myself.
Dear Richard,
I am a PhD student with very little experience on statistics. We have a prototype medical device for breast imaging. I am interested in the reliability of this system: I want to know that if I measure the same thing 10 times, whether I get 10 times the same result. In order to test this, I can make use of phantoms or test objects, which I take an image of and then calculate a metric for image quality, for example contrast. These test objects are in principle stable, so with a perfect system I should measure 10 times the exact same contrast.
Now I want to know how many of these test objects I should measure, and how many times each; and what form of ICC I should use. The situation is a bit different from what you are describing with raters and ratees. Is it right to ‘replace’ the term raters to test objects in our situation? And then ratees = measurements or images? Or the other way around?
Then, my thoughts are to use a two-way-random model. One test object might for example return a much higher value for contrast than another object, so they could be considered random.
Could you please comment on this and let me know if you think I am on the right track? I have just started reading on statistics for this purpose, so I might be thinking in the wrong direction.
Thank you,
Marije
ICC as a general concept can reflect one of two things: what is the proportion of “true” variance represented by a single score (ICC[#,1]) or the proportion of “true” variance represented by a mean (ICC[#,k]). In your case, you seem to want to know the true variance captured by a single use of your device. So we’re halfway there.
The next issue is: what contributes meaningful variance you are interested in getting to that question? Differences between test objects should be more-or-less random and should not affect reliability conceptualized this way. For example, if one image has high contrast and another has low contrast, you want to detect that contrast consistently, but the fact that one is low and the other is high is irrelevant. That means your case set is this population of rating targets, i.e., ratees = test objects.
A rater therefore is a pass through your system, i.e., if you re-create the same process from start-to-finish for each case, is your device consistent when run across those images? Thus, you need to repeat the full recording process from start to finish and see how consistent your device is across those uses. You didn’t give many details on how your device works, but to assess reliability, you might do something like take 10 images of the same breast and then process them from start to finish using your device.
Doing this on test images could remove a potential source of meaningful variance, which is likely to introduce bias. But you’ll need to carefully work through this for your project. For example, let’s say I had a device that could take a blood sample and detect the presence of blood-molecule-A (BM-A). There are two reliability questions at play – one, if I run a single sample through my device 10 times, is it consistent? And two, if I collect 10 samples of blood from the same patient 10 times, are those consistent? Usually, the second question is far more important, but it depends on exactly what you want to know.
In either case, the 10 measurements you take are the “raters,” i.e., you have used your device 10 times to see how consistent things are across the 10. In both of these cases, there is no particular population of measurements you are assessing. Conceptually, the 10 times are completely interchangeable, i.e., random possible measurements. Thus, you need one-way-random.
All together, that means you most likely want to examine: one-way-random single raters, i.e., ICC[1,1]
The one potential hitch here is that ICC in general assumes normally distributed data. You say in your description that you expect “the exact same” rating each time. ICC is not designed to handle cases like this – if you have 10 ratings that are all “3”, then there is no variation within the 10 ratings, and ICC’s assumptions are broken. If you look at your data and notice this sort of pattern, i.e., all 10 ratings are usually the same number yet you’re getting a low ICC, this is probably what’s happening. In this case, you’re better off using a more conservative estimate of agreement, e.g., something like “in what proportion of cases do all 10 ratings agree?” This is still a reliability estimate, even if it seems simple. The primary advantage to ICC is that it controls for external sources of variance associated with randomness. If you don’t have much randomness, you don’t really need ICC.
As for “how many raters/samples of each image and cases/images do I need,” this is driven by how much certainty you want for your estimate. If for example you conduct your rating study with 3 samples and they are usually very similar, you won’t need as many cases to get a consistent reliability estimate versus if they are very noisy. The only way to determine this absent existing data is a pilot study. So you might for example ballpark it (let’s say you try 5 raters/re-tests) and get a small sample of cases (let’s say 15) and see what ICC looks like in that sample. Then use those results to inform your next step – you will definitely want more cases, but you might need a smaller or larger number of raters, depending on the results of your pilot.
Dear Mr. Landers,
Sorry if this question has been asked before. In my case, three nurses have measured a couple of variables on the same four patients, each nurse has done it three times separated by equal time intervals. I have been asked to measure interrater reliability (between nurses) and the concordance for each nurse. As I understand to measure reliability between nurses I should use ICC, but since there are repeated measurements, should I average them to get one variable per nurse? Can I use ICC for each nurse using in each case the repeated measurements as variables/columns?
Thanks in advance.
It depends. Do you believe time to contribute meaningful variance to scores, i.e., do you expect nurses to always make exactly the same judgment per case, regardless of time? Or in other words, do you expect the patients to never change over time? My suspicion is that you do expect patients to change over time, which means that variance over time is a confound to reliability measurement. In this case, you need to control for time. The simplest approach is what you describe – to look at ICC for each time separately and then calculate an average. The more “correct” way to do it is with hierarchical modeling, so that you can control for time explicitly. Calculating it as an average across 3 ICCs will potentially give you an underestimate of reliability, although that’s dependent on a few other data characteristics.
Hi Dr Landers,
can u give examples of intra-raters and inter-raters hypothesis? I don’t know how to write the hypothesis for both of them and it’s quite challenging to find an example from the internet. I’m doing ICC(3). Thank you for your help.
I suspect you aren’t finding examples because that’s a pretty unusual thing to want to do.
Assuming you are talking about null-hypothesis significance testing, there is only one possible null hypothesis: there is no effect/relationship. Thus, the hypothesis pair in either case is:
H0: Intra/interrater reliability is zero.
H1: Intra/interrater reliability is not zero.
Significance testing tells you nothing about the magnitude, importance, value, replicability, etc of your reliability estimates. It only tells that if the population reliability were zero, the reliability you observed was either probable or improbable. So be careful to determine if that’s really what you want to know and demonstrate.
Dear Dr Landers,
Very nicely explained topic!
I want to know if the ICC can be used to determine inter-and intra-subject variability in one step. For example, if I create a physical object for quality control of an imaging system, build this object twice and make test-retest measurements. Can I use a single ICC to say that both the model created is repeatable and that the measures from test-retest will be always the same for both objects? If that is not correct, what would you recommend me to use for the evaluation of the inter-and intra-subject variability in this case?
Also, I was wondering if you have a post like this on the coefficient of variation.
Thanks,
Alejandra
An ICC is by definition a single estimate of consistency – it’s the research design / choice of data modeled that drives what you can conclude from it. In your case, you essentially have a hierarchical analysis, i.e., test-retest is nested within model. In that case, you’d still want to use ICC to assess test-retest consistency but you would probably want to examine model effects separately, as a between-subject effect. In other words, you’d probably want to do it all within one multilevel model (HLM), but you’d have one estimate for each aspect of reliability. All reliability estimates can be thought of as “consistency of x while ignoring inconsistency in y”, so you need to pick x and y explicitly and then model given those decisions.
SPSS no longer specifies in the output if it is computing a single measure or average measure ICC … I definitely want the average measure test but can’t find any information about how to be sure I get that test using SPSS 27 …
Dear Richard
Thank you very much for your clear explanation.
I have 6 candidates (Cases) and 10 evaluators (raters)
When apply Intraclass correlation in SPSS as you clearly explained, the Cronbach’s alpha value is coming as negative values due to the average negative covariance.
Is the hypothesis testing for correlation is valid at this moment?
A negative ICC usually indicates inadequate within-groups variance to meet the assumptions of the ANOVA that underlies ICC calculations. I would instead recommend changing to simple percentage agreement approach (or chance-corrected agreement, like a kappa).
Hi Richard,
Your guidance on inter-rater reliability is so helpful.
I am wanting to compare the scores awarded on three sepecific assessment measures by an assessor (rater 1) and a moderator (rater 2) on the same 27 candidates. I have chosen a random selection of assessors (within a limited pool of assessors) to moderate/second score, so rater 1 varies but myself as rater 2 is constant for all 27 candidates compared. I am interested in the absolute scores (so whether the exact same score is given to a candidate by the assessor and moderator).
I’ve been researching but I can’t seem to find the answer about whether it’s appropraite to use ICC when the raters are a mix of consisent and varied.
Any guidance would be really helpful.
Thanks,
Lucy
I’m not 100% on the details here, but if you have a gold standard rater (you?), reliability as ICC calculates it (i.e., shared variance between raters) isn’t a meaningful concept – you should be more interested in congruence versus the gold standard rater. You would better off with natural-scale estimation, e.g., calculating the average disagreement between raters. If you are still both conceptually from a single population of raters (not sure from your description), then ICC is still appropriate BUT if you don’t have any variance among your ratings, you are breaking an assumption of ANOVA (the test underlying ICC) in that each rater (conceptually an ANOVA group) will not contain normally distributed ratings. So I would still not use ICC in this case, but only because it will probably attenuate your ICC pretty severely.
So, I have 3 readers and have read reports for different samples. What method of ICC would that be Check for reliability?
Could be almost any of them. You’ll need to answer the questions in the article to determine that.
Hi Richard,
Thank you so much for the detailed article (and subsequent comments) on using ICC. As a student, t’s been really useful to explore what the different ICCs mean and which ones you should use in specific circumstances. I wondered if I could ask a couple of extra clarifying questions?
1. Am I right in thinking that single rater and average measures are likely to give very different ICCs (with average ICCs larger than single)? Whilst neither are superior than the other, I’m guessing in literature reviews it would be better to compare single rater to single rater and average measures to average measures otherwise one may seem somewhat inflated/deflated to the other?
2. I have also seen a double-entry ICC (DE) being reported. Would you provide some context on where this sits within the model/when it would be appropriate to use please?
Thanks again for all your help!
Average ICC will always for mathematical reasons be larger than single-rater ICC. Single-rater ICC is actually calculated as an estimate from the multi-rater ICC, by simulating the reliability of a hypothetical “average” rater among the raters you did actually collect. The two numbers can be similar in certain circumstances. For example, if a single rater is already highly reliable (e.g., .95), adding raters is not going to increase reliability dramatically. Further, if a single rater is highly unreliable (e.g., .01), then adding a small number of raters is not going to help much (e.g., if one rater is .01, two raters will probably be .02). The largest differences will be observed when a single rater is modestly reliable (e.g., .3) and then you observe a large number of raters (e.g., with ICC(k,1) = .3, your ICC(k,50) would probably be close to .99). Importantly, ICC(1,k) is not an “Average ICC” but rather “ICC of the average,” so this implies that cramming more, good information into your ICC (e.g., by taking an average across a large number of good raters) is where the greatest benefits will be observed.
I had never heard of double entry ICC before your post, and in looking it up, it does not appear to be a mainstream approach, and there’s some disagreement even as to its definition. One piece I found defined it as a double-entry Pearson’s correlation, which is a way to correct downward for arbitrary ordering in a Pearson’s correlation. My guess is that procedure would make a ICC(DE) conceptually similar to a consistency-basis ICC(1,k). But I don’t know much about it beyond that, unfortunately.
Thank you so much, Richard. This is a really helpful explanation.
Hello Richard,
I am a student and researching the interrater and intrarater reliability of surgeons assessing angiographies. I’m using SPSS statistics program.
I have 7 raters that assess the same 15 angiographies at 3 different time points, whilst assessing different variables (e.g. would you treat the lesion, which diameter is the lesion in mm).
For the interrater reliability it seems to bring the results that I am interested in. I put in all 45 assessments (15 angiographies x 3 assessments) and calculated the ICC using two-way mixed absolute agreement. This seems to work.
However, I am struggling to determine the intrarater reliability per rater. I expect them to answer the questions in the same manner each time (as I’m asking them which diameter the vessel would be, time would not be a factor that changes the diameter of the vessel or if they would treat the lesion). Can I analyze this in the same manner I would with the interrater variability, but using the 3 measurements of the same observer? Or should I use a different test as you would not be able to use the ICC for just 1 observer that made 3 observations?
I have tried to do this (two-way mixed, absolute agreement) for the raters individually, however the results do not correlate with the eyeball results (just screening the data, e.g. I expected observer 1 to have a poor agreement as they put in different answers compared to observer 3).
I hope this was clear, thank you in advance.
Kind regards
I am not sure you have calculated the reliability estimate you think you have. Are you trying to estimate the reliability of raters at specific time points, or the reliability of raters across all time points simultaneously? If specific time points, you should have 15 rows and 7 columns per time point, i.e., three different estimates of interrater reliability, one for each time point.
If I understand the way you have done it from your description, i.e., 15 rows and 3 columns, you are not estimating inter-rater reliability at all and are only examining inter-test reliability in the estimate you have produced.
In all cases, remember that the goal is to put the different sources/causes in columns and independent ratings from each of those sources in rows. Anything else and you are likely confounding something.
Hello, Richard.
I want asked, is there any chance that Single Measures lower than Average Measures? As example, the single is around .44 and the average is around .91. I measured a module for clinical theapy and rated by three specific rater. So, I used Two-Way Mixed and consistency. If the Single Measures has lower number and it has big gap compared to the Average Measures, why was the reason?
Thank you in advance, have a nice day!
Single is always less than average, because single is calculated by 1) assuming that every rater is of the same quality, and 2) estimating the reliability of a single rater given however many raters you actually had. So in your case, the reliability of the mean of your three raters is .91, and you would expect a reliability of .44 if you only had one rater making ratings on each case. You can also use the Spearman-Brown prophesy formula on either value to calculate other values, e.g., to see if 2 raters would be likely to meet an acceptable reliability standard in future ratings.
Dear Richard,
I am currently doing a validation study to compare two software packeges for analysing certain microscopyic images. For each subject included in my study 3 measurements at 5 different exactly defined timepoints during an operation were gathered. I have 3 variables of interest which are all continuous. I want to know the reliabilty of software A (goldenstandard) vs software B (index). I want to use ICCs to do so. I though ICC two way mixed, singel rater, absolute agreement, would be the correct ICC model for this scenario.
I have 2 questions about ICCs in this particular situation.
1. One of my 3 variables of interest is non-normally distributed, but skewed left. Since ICCs are usally calculated by ANOVA, which has the assumption of normally distributed data, I deducted that data for ICC calculation needed to be normally distributed. Therefore, I transformed the data of variable of interest P by reflecting it and the sqrt it.
I thought that to calculate an ICC I had to do this for both software analysing methods (both raters). But how do I interpret the ICC calculated after this transformation? Or should I try to find another way to calculate reliability for this non-normally distributed variabele P?
2. My data has repeated measures. Every indivivual is measured 3x and 5x points in time. Is ICC still the correct way to assess reliability when there are repeated measures? Or is there a better solution?
Thanks in advance for your time and help.
Kind regards,
Jord
ICC is only going to be appropriate as a measure of interrater reliability if you have normally distributed data and independence of cases. Without normally distributed data, ICC will be biased. That doesn’t necessarily mean you can’t use it, but rather you should keep this in mind when trying to interpret its meaning (i.e., skew can create upward OR downward bias, and you have no way to know which). The severity of bias will be proportional to skew severity, so if you have relatively little skew, it probably doesn’t matter much.
In terms of the repeated measures problem, I would suggest you do use ICC but that you don’t calculate the way I describe here. A better approach is to calculate ICC within the context of a mixed effects models, i.e., to treat it explicitly as multilevel data and model it that way. There are many specific methods to do this, but none of them can be done easily in SPSS to my knowledge. These days, I typically use lmer() in R – it will output an ICC for any multilevel model you specify. In such a case, you are calculating the ratio of between groups to total variance considering the groups (i.e., individuals in your case) either controlling for time (i.e., the conditional ICC) or assuming any effect of time is random error (i.e., the unconditional ICC).
Dear Dr. Lander,
First of all I would like to thank you for your work and patience with novice researchers like myself. I come from the animal production sector, where my previous utilization of statistics has been relatively simple, using different ANOVA, Pearson’s, Tukey, PCA, among others. However, as I delve into more complex statistical analyses, I find myself in need of guidance.
While working on my recent paper, I found a study that employed the Interclass correlation coefficient (and Kendall’s W) for similar data to mine. This discovery has prompted me to consider its applicability to my research. Despite having reviewed numerous papers in my field, these statistical analyses have not been commonly employed, leading me to question their relevance in my context.
My research focuses on assessing the endurance of chickens subjected to a sprint test, aiming to understand the variability and its molecular-level effects. The experimental design involved randomly selecting 24 chickens from a group of 200 with identical characteristics (same producer, age, diet). These chickens underwent an endurance test on two occasions: one day (D1) in the morning (MT) and evening (ET), and the same procedure was repeated 15 days later (D15). The study factors include day and time slot, each with two levels (D1, D15; MT, ET), along with their interaction. Consequently, my experimental groups were categorized as D1-MT, D1-ET, D15-MT, and D15-ET. Employing a repeated measures two-way ANOVA for the analysis of the four data points collected from each animal, I observed a notable improvement in response during the evening compared to the morning and an overall enhancement after 15 days.
My specific concern is whether I can appropriately apply the Interclass correlation coefficient (ICC) in this case. Should it be one-way or two-way? Absolute or consistency? Single or average rater?
As an illustration, a sample of the data for Animal X (D1-MT, D1-ET, D15-MT and D15-ET), recorded in arbitrary units:
Animal 1: 3, 3.4, 3.3, 3.6
Animal 2: 2.5, 3, 3.2, 3.4
Animal 3: 2, 2.2, 2.2, 2.5
Animal 4: 2.8, 3, 3.2, 3.3
…
Animal 24: 2.9, 2.9, 3.3, 3.4
Thank you so much for your help and time
Sincerely, Eugene
My answer would depend on your answers to the questions I describe in the article, plus quite a few more questions.
For example, do you consider time a random factor? Or in other words, is measurement in the morning vs the evening irrelevant, or do you expect there to be some effect of time of day? In the first case, you are treating time as error, which means you could consider each sprint test independent as least in relation to time. In that case, ICC would make sense. If instead you believed that time of day might have a causal effect on sprint test results, you are treating time as an effect, which means you would want to treat sprint tests within each time as a unique type of information, i.e., one ICC per sprint test.
From what you’ve written, it sounds like you are studying time as an effect, i.e., you observed an improvement in the evening. That suggests to me that you only have 1 observation per chicken per effect combination, i.e., no duplication of measurement, which makes it impossible to assess reliability using ICC or anything else.
On the other hand, if you consider the chickens themselves to be independent, i.e., the 24 chickens are interchangeable in their interactions over time (e.g., if chicken 4’s performance on day 1 is completely unrelated to chicken 4’s performance on day 2 beyond the general effect of time passing), then you might conceptualize reliability as agreement within each time point across chickens. On yet another hand, if you don’t consider them independent, you probably don’t want to use ICC at all here and should instead explicitly use a multilevel modeling framework so that you can separate the effects of day, time, and chicken identity.
In short, there are a lot of “it depends” in the answer to your question! I hope this helps you work through some of them.